Engineering Mechanics: Unit III: Distributed Forces
Pappus-Guldinus Theorems
with Solved Example Problems
The two theorems of Pappus and Guldinus are used to find the surface areas of surfaces of revolution and volumes of bodies of revolution.
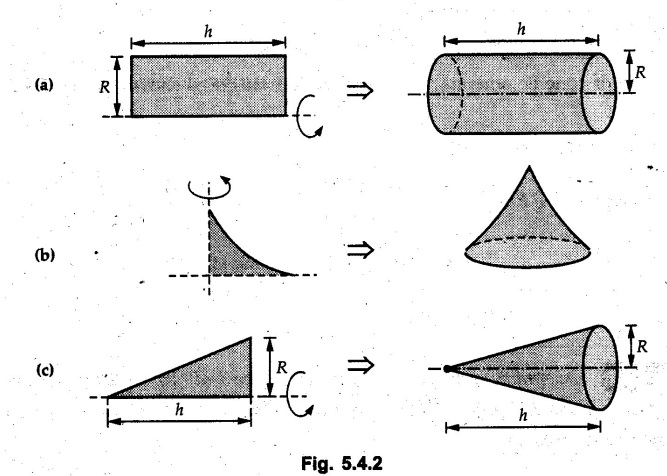
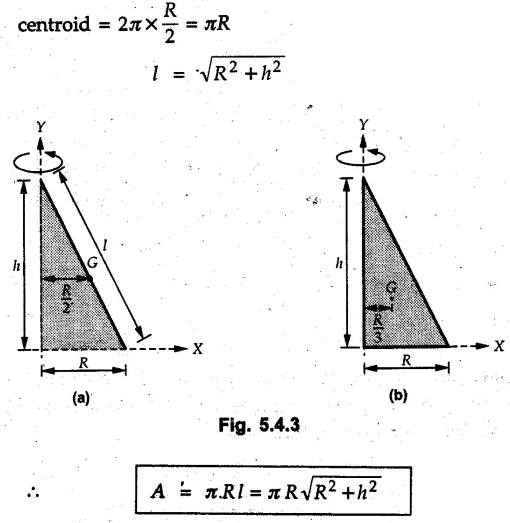
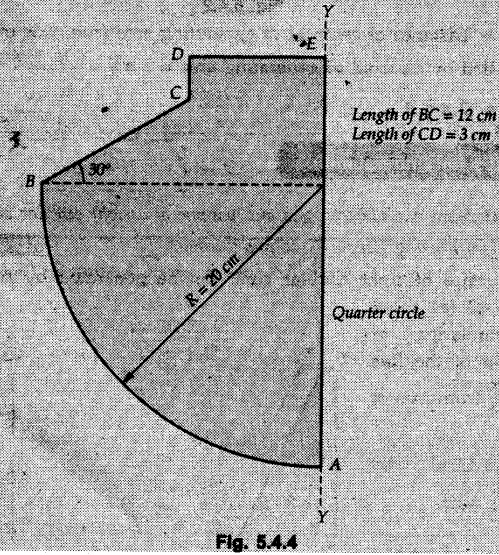
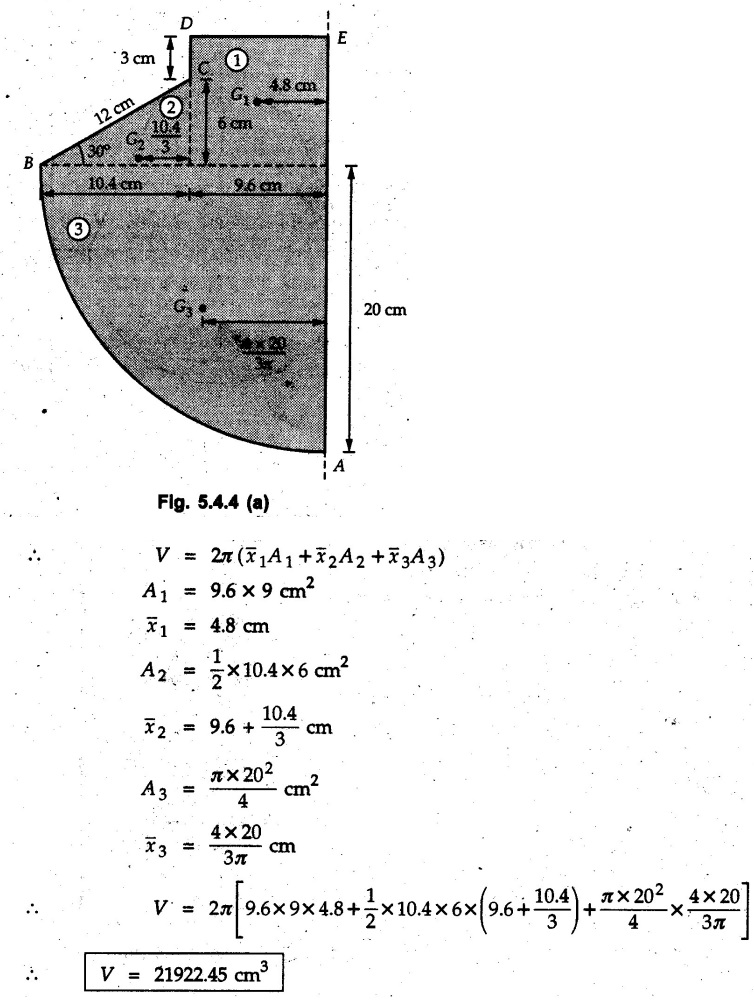
Pappus-Guldinus Theorems • The two theorems of Pappus and Guldinus are used to find the surface areas of surfaces of revolution and volumes of bodies of revolution. • Surfaces of revolution can be generated by revolving any curve (or line) about any axis. • For example, a straight line when rotated about a parallel line generates the surface of a cylinder as shown in Fig. 5.4.1 (a). An inclined line generates a cone as shown in Fig. 5.4.1 (b) and a quarter circle generates a hemisphere as shown in Fig. 5.4.1 (c). • Bodies of revolution are obtained by revolving areas about an axis. A few examples are shown in Fig. 5.4.2. • The first theorem is used to find the area of a surface of revolution. Theorem I: The area of surface of revolution is equal to the product of length of the generating curve and the distance travelled by the centroid of the generating curve while generating that surface. • If the centroid of a generating curve of length l is at distance • Distance travelled by centroid = Theorem II: The volume of a body of revolution is equal to the product of generating area and the distance travelled by centroid of the generating area while generating that volume. If A = Generating area and Distance travelled by centroid of generating area = Example 5.4.1 Determine the surfaces area and volume of a right circular cone with radius of base R and height h using Pappus-Guldinus theorems. Solution: The surface of right circular cone can be generated by revolving a line as shown in Fig. 5.4.3 (a) about Y-axis. By similarity of triangles, centroid of the line is at a distance R/2 from axis of rotation. Distance travelled by The volume of cone is generated by revolving a triangle as shown in Fig. 5.4.3 (b) about Y-axis. Distance travelled by centroid = 2л R/3 Area of triangle = 1/2 Rh Example 5.4.2 Determine volume of revolution generated by revolving plane lamina ABCDEA shown in Fig. 5.4.4 about Y-Y axis, to 2л rad. Write statement of theorem used for calculating volume. Solution: According to Pappus-Guldinus theorem, the volume of body of revolution is product of the generating area and the distance travelled by centroid of the generating area while generating that body. (Here distance of centroid from Y-axis is The given area can be divided into 3 parts – 1) A rectangle 2) A triangle and 3) A quarter circle (Refer Fig. 5.4.4 (a)) Example 5.4.3 Find surface area of the glass to manufacture an electric bulb shown in Fig. 5.4.5 using first theorem of Pappus-Guldinus. Solution: As surface area of only glass is required, we do not consider the aluminium holder. The glass surface can be generated by revolving the curve shown in Fig. 5.4.5 (a)) about the vertical axis. Example 5.4.4 Calculate the volume V of the solid Fig. 5.4.6 generated by revolving the 60 mm right triangular area through 180° about the z-axis. Solution: By Pappus - Guldinus theorem, V = Generating area × Distance travelled by centroid of generating area Generating area = 1/2 × 60 × 60 = 1800 mm2 Distance travelled by centroid of generating area = ⸫ V = 1800 × 157.08
![]() from the axis of rotation,
from the axis of rotation,

![]() = Distance of centroid of generating area from axis of rotation,
= Distance of centroid of generating area from axis of rotation,

Solved Examples for Understanding
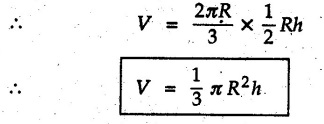

![]() )
)
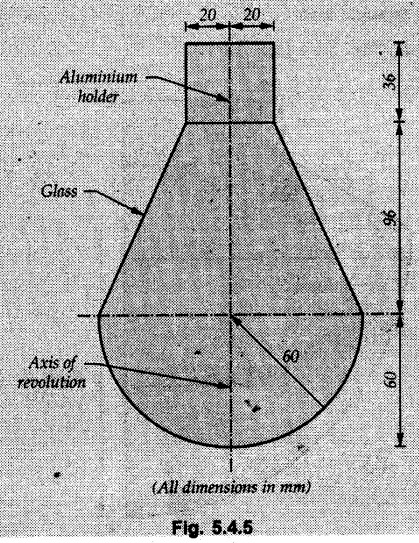
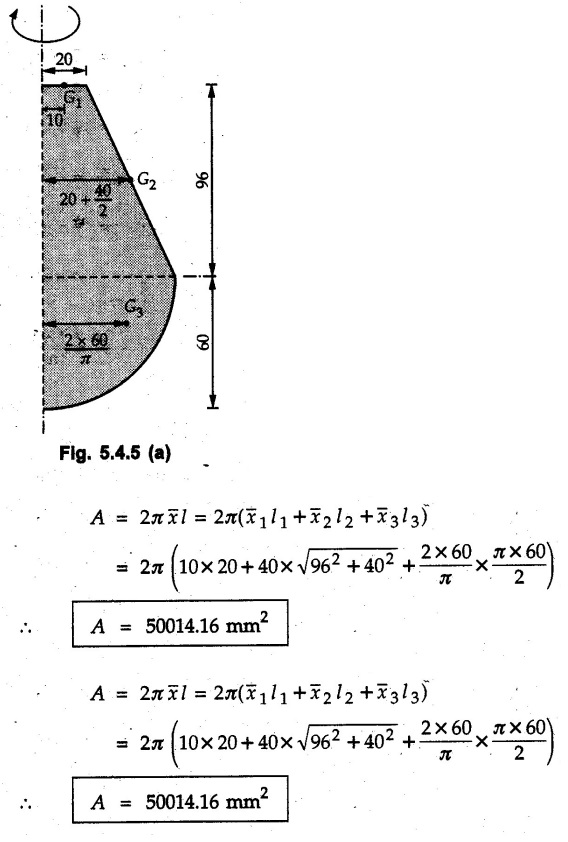
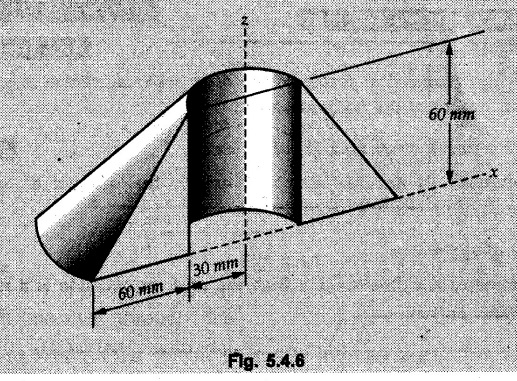
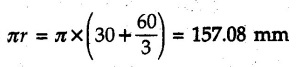

Engineering Mechanics: Unit III: Distributed Forces : Tag: : with Solved Example Problems - Pappus-Guldinus Theorems
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
