Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics
Momentum Equation
Fluid Mechanics
The momentum equation is one of the basic tools for finding the solution of flow problems.
MOMENTUM EQUATION The momentum equation is one of the basic tools for finding the solution of flow problems. Its application leads to the solution of problem in fluid mechanics which can't be solved by energy principles alone. Sometimes it is used in conjunction with the energy equation to obtain complete solution of engineering problems. The momentum equation is based on the law of conservation of momentum. It's say that the net force acting on a mass of fluids equal to change in momentum of flow per unit time in that direction. From the Newton's second law of motion Force (F) = mass of fluid (m) x acceleration (a) Acceleration (a) = dv/dt Where dv = change in velocity dt = change in time F = m × (dv/dt) F = {d (mv)}/dt (m is constant and can be taken inside the differential) The above equation is known as momentum principle. F.dt = d(mv)is known as momentum equation or impulse momentum equation The impulse of a force (F) acting on a fluid mass (m) in a short interval of time (dt) is equal to the change of momentum {d(mv)} in direction force. Applications: ✓ To determine the resultant force following boundary surface ✓ Pipe bends ✓ Reducers ✓ Moving vanes ✓ Jet propulsion etc., ✓ To determine the characteristics of flow when there is an occurance of change of flow in varying cross section. ✓ Sudden enlargement in pipe. ✓ Sudden contraction in pipe ✓ Hydraulic jump in channel etc., Assumptions: ✓ The liquid is ideal and incompressible ✓ The flow is steady and continuous Let as consider one such stream tube lying in the X-Y plane and having steady flow of fluid as shown in figure 1.29. Flow can be assumed uniform and natural to the inlet and outlet areas. Here V1 - velocity of entrance section 1-1 A1 - area of entrance section 1-1 ρ1 - density of entrance section 1-1 V2, A2 and ρ2 are corresponding values at section 2-2. The mass of fluid in the both region 1-1and 2-2 shifts to new positions 1'-1' and 2'-2'due to effect of external force on the stream after a short interval. Due to gradual increase in the flow area in the direction of flow, velocity of fluid mass and the momentum is gradually reduced. The changes in moment of the fluid masses in the sections 1-1 to 1'-1' and 2-2 to 2'-2' have to be considered because the sections 1'- 1' to 2-2 containing liquid is unaffected due to same cross sectional area. According to the principle mass concentration, Fluid mass with region 1-1 to 1'-1' = Fluid mass with region 2-2 to 2'-2' Density × Volume = Density × Volume ρ1 × A1 × ds1 = ρ2 × A2 × ds2 where ds1 and ds2 are change in length for the corresponding region of fluid. ρ1 × A1 × V1 × dt = ρ2 × A2 × V2 × dt here ds1 = V1 × dt and ds2 = V2 × dt ρ1 = ρ2 = ρ A1 × V1 = A2 × V2 = Q Hence (ρ × Q × dt) = (ρ × Q × dt) Mass of fluid is same in both sections. Change in momentum = change of mass of fluid x change of velocity of fluid = (ρ × Q × dt) × (V2 − V1) = ρ × Q (V2 − V1) × dt Using impulse momentum equation, Acting force with respect to time = change of momentum F.dt = ρ × Q (V1 - V2) × dt F = ρ × Q(V1 - V2) Where ρ × Q is the mass of flow per second and is called mass flux. The momentum equation is used to find out the resultant force exerted by a flowing fluid on pipe bend. Consider two sections 1 and 2 as shown in figure 1.30. V1 - Velocity of flow at section-1 P1 - Intensity of pressure at section -1 A1 -Area of cross section of pipe t section -1 V2, P2 and A2 are corresponding values at section-2 F1 and F2 be the components of the forces exerted by the flowing fluid on the bend in x and y directions respectively. The forces exerted by the bend on the fluid in the directions of x and y will be equal to Fx and Fy but in opposite direction. The other external forces acting on the fluid are P1 A1 and P2A2 on the sections (1) and (2) respectively. The momentum equation in x-direction is Net force acting on fluid in (x) direction = Rate of change of momentum in x direction P1xA1 - P2x A2 - Fx = ρ x Q (V2x - V1x) -Fx = ρ x Q (V2x - V1x) – P1x A1 + P2x A2 Fx = ρ x Q (V1x – V2x) – P1x A1 - P2x A2 F1 =pxQ (V1 P1x - initial pressure in x- direction P2x - final pressure in x - direction V1x - initial velocity in x - direction V2x - final velocity in x - direction Similarly Ey = ρ x Q (VIy – V2y) + PIyAI – P2y A2 PIy, P2y , VIy, V2y are corresponding vaines in y-direction Components along x-axis = V1 cosθ1 and V2cos θ2 Components along y-axis = V1 sinθ1 and V2sinθ2 From the above mentioned fiqure V1x = V1 because no bend V2x = V2 cos θ because outlet is bend pipe V1y = 0 because no initial velocity in y-direction. V2y = V2y sine because pipe is bend in y-direction Hence Fx = ρQ (V1x -V2cosθ) + P1x A1 – P2x A2cosθ Similarly Fy = ρQ (0 - V2y sinθ) + 0 − P2y A2sinθ = ρQ (-V2ysinθ) – P2y A2 sinθ Resultant force Angle made by the resultant force with horizontal direction is given by1. Impulse momentum equation
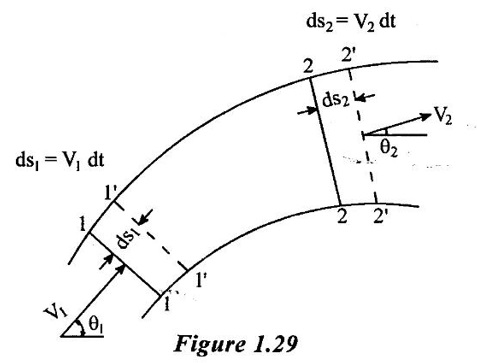
2. Forces exerted by a flowing fluid on a pipe bend
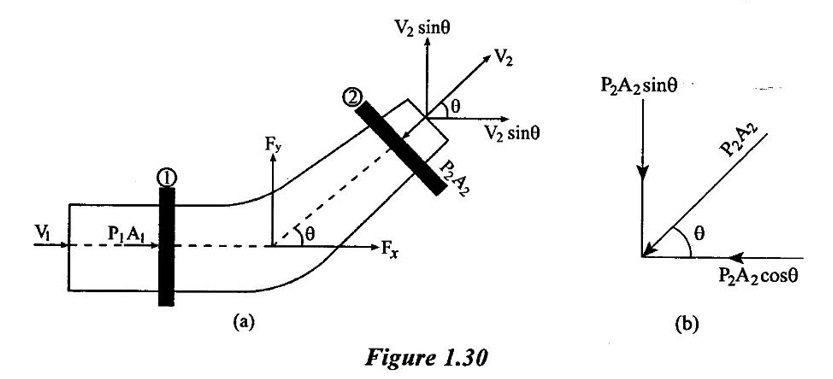
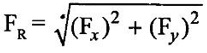
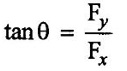
Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics : Tag: : Fluid Mechanics - Momentum Equation
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
