Engineering Mechanics: Unit III: Distributed Forces
Moment of Inertia of Plane Area
The moment of inertia or second moment of a differential element of area dA about the X-axis is defined as the product of its area and the square of its distance from X-axis i.e.,
UNIT - III Area Moment of Inertia Syllabus Determination of the Moment of Inertia of an Area by Integration, Polar Moment of Inertia, Radius of Gyration of an Area, Parallel - Axis Theorem, Moments of Inertia of Composite Areas. • The moment of inertia or second moment of a differential element of area dA about the X-axis is defined as the product of its area and the square of its distance from X-axis i.e., • The distance of the differential element of area dA from the X-axis is y as shown in Fig. 6.1.1. • The moment of inertia of the area A about X-axis is obtained by integrating equation (6.1.1) to cover the complete area. Similarly the moment of inertia about Y-axis is • The moment of inertia of the area about an axis perpendicular to its plane is known as polar moment of inertia. For the area shown in Fig. 6.1.1, the polar moment of inertia is about the Z-axis. As the area dA is at a distance r from Z-axis, • The moment of inertia is always a positive quantity, irrespective of the sign of x or y as it involves the squares of these quantities. • The S.I. unit of moment of inertia is m1. More commonly, the unit mm1 is used due to smaller dimensions of the areas of cross-sections of beams and shafts used in actual practice.Moment of Inertia of Plane Area



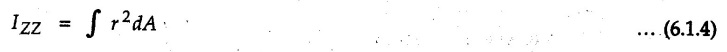
Engineering Mechanics: Unit III: Distributed Forces : Tag: : - Moment of Inertia of Plane Area
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
