Engineering Mechanics: Unit III: Distributed Forces
Moment of Inertia by Integration (From First Principles)
The moment of inertia can be obtained by choosing an appropriate differential element dA which can be either rectangular or a horizontal or vertical strip writing its moment
Moment of Inertia by Integration (From First Principles) • The moment of inertia can be obtained by choosing an appropriate differential element dA which can be either rectangular or a horizontal or vertical strip writing its moment of inertia and then integrating to cover the whole area. This procedure is illustrated for some standard figures. • Consider a rectangle of dimensions b×d as shown in Fig. 6.5.1. Consider an elemental strip of length b and width dy at a distance y from the centroidal X-axis. • The moment of inertia about the base AB can be obtained using parallel axes d theorem. The distance of AB from X-X axis is d/2. • The polar moment of inertia can be obtained using perpendicular axes theorem. • The radius of gyration about any axis can be obtained using • Consider a triangle of base b and height h as shown in Fig. 6.5.2. Choose a horizontal strip of length b and width dy at distance. y from the base as the differential element. By similarity of triangles, • Moment of inertia of the strip about the base is, • The centroid of triangle is at a height of h/3 from the base AB. Using parallel axes theorem, • The radius of gyration about centroidal axis is • Consider a circle of radius R. Choose a differential element of angular width dθ at angle θ and radial width dr at distance r from the centre as shown in Fig. 6.5.3. • The distance of this area element from centroidal X-axis, which is the diameter, is y = rsin θ • The polar moment of inertia is • Consider a semicircle of radius R as shown in Fig. 6.5.4. • Choose differential element of angular width dθ at angle θ and radial width dr at distance r from the centre. • The area of the differential element will be dA = (rdθ) (dr) ⸫ dA = rdr dθ • The distance of this differential element from the diameter AB is y = rsinθ • M.I. of differential element about AB is, • The centroid is at a distance of 4R/ Зл from AB. • The moment of inertia about a centroidal axis perpendicular to diameter (Y-axis shown in Fig. 6.5.4) is • Consider a quarter circle of radius R as shown in Fig. 6.5.5. • Choose a differential element of angular width dθ at angle θ and radial width dr at distance r from the centre. • The area of the differential element will be, dA = (r dθ) (dr) ⸫ dA = r dr dθ • The distance of this differential element from AB is y = rsinθ • M.I. of differential element about AB is1. Rectangle



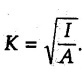 Here, A = bd
Here, A = bd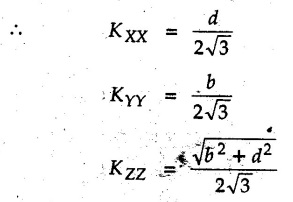
2. Triangle
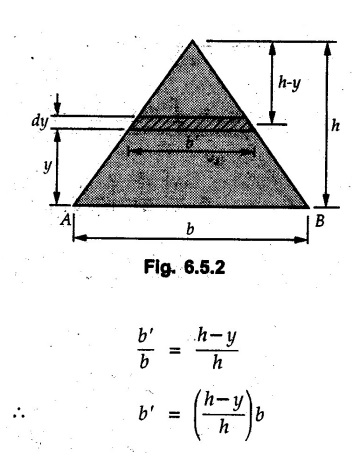


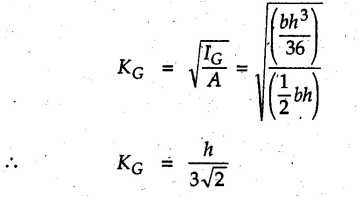
3. Circle
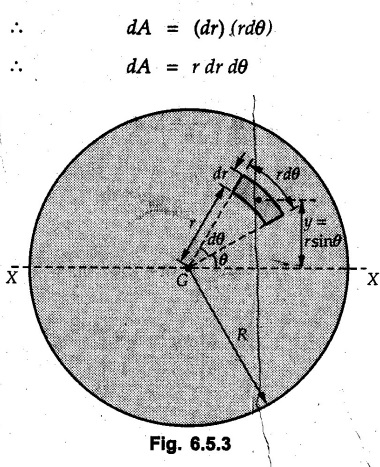


4. Semicircle


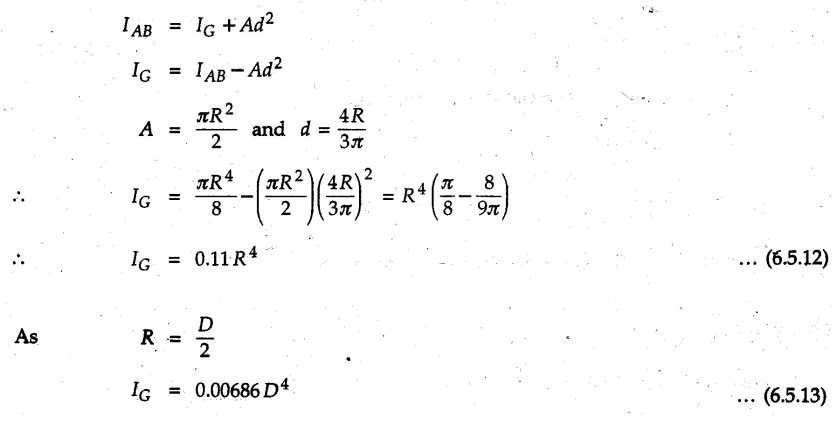
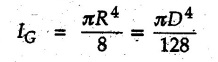
5. Quarter Circle


Engineering Mechanics: Unit III: Distributed Forces : Tag: : - Moment of Inertia by Integration (From First Principles)
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
