Maxwell's Equations

MAXWELL'S EQUATIONS

Faraday laid the foundation of electromagnetism. He suggested the possibility of the propagation of electromagnetic waves through space. The idea was later confirmed and fully developed by Maxwell who expressed the laws of electromagnetism in terms of fundamental equations.

He showed that electromagnetic waves can be produced by changing electric and magnetic fields. Maxwell's equations form the foundation of electromagnetic theory.

Maxwell's Equations (Derivation)

There are four Maxwell's equations in electromagnetic theory. The first two equations are known as steady state equations and the last two equations are known as time varying equations.

Maxwell's Equation - I (From Gauss's law in electrostatics)

Integral form

Gauss's law in electrostatics states that the total electric flux through-any closed surface is equal to the charge enclosed by it (Fig. 2.1).

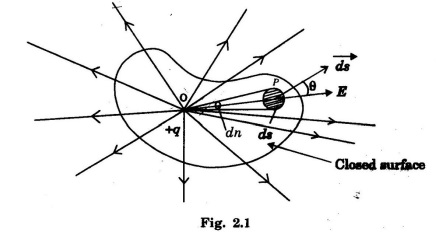
According to Gauss law,

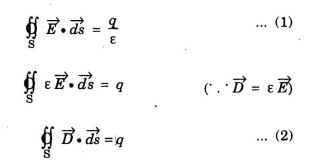
Now, if ρ is the charge density, (charge per unit volume) then total charge inside the closed surface is given by

Substituting eqn (3) in eqn (2), we have

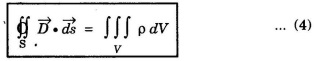
This is Maxwell's equation in integral form from Gauss law in electrostatics.

Applying Gauss's divergence theorem to LHS of eqn (4), we get

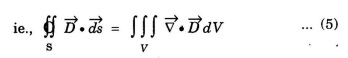
on substituting eqn (5) in eqn (4), we get

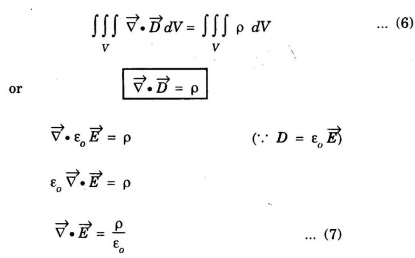
This is Maxwell's equation from Gauss's law electrostatics in differential form

Statement

The total electric displacement through the surface enclosing a volume is equal to the total charge within the volume

Maxwell's Equation - II 

(From Gauss's law in magnetostatics) 

Integral form

It is a well known fact in magnetism that the magnetic lines of force are continuous and do not appear to have the origin or the end. Thus the total magnetic flux through any closed surface in a magnetic field is zero ie.,

This is Maxwell's equation in integral form from Gauss's law in magnetostatics.

Applying Gauss divergence theorem to the L.H.S. of equation (1), We get

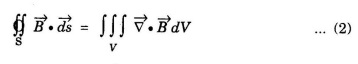
on substituting eqn (2) in eqn (1), we have

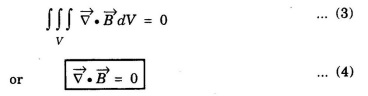
This is Maxwell's equation in differential form from Gauss's law in magnetostatics.

Statement

The net magnetic flux emerging through any closed surface is zero.

Maxwell's Equation - III 

(From Faraday's law)

Let us consider C be a closed circuit and S be the surface with C as its boundary (Fig. 2.2). Let B be the magnetic flux density inside the closed circuit.

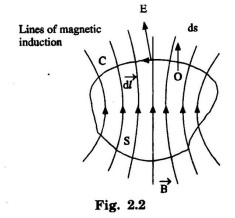
Magnetic flux through a small area ds =

⸫ Total magnetic flux linked with the circuit =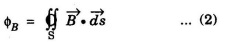

Faraday's law states that the induced emf is the rate of change of magnetic flux ϕB

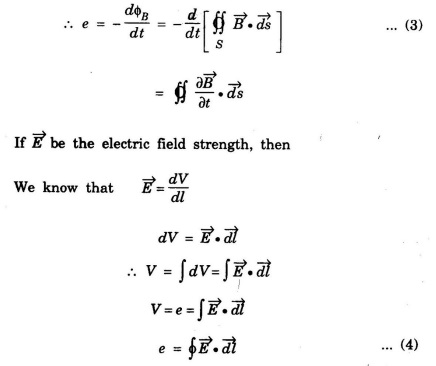
Here, the integral is taken over a closed curve C. 

Equating eqn (3) and eqn (4), we have

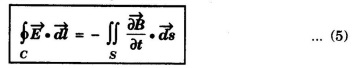
This is Maxwell's equation in integral form from Faraday's law of electromagnetic induction. 

Now, applying Stoke's theorem to L.H.S. of eqn (5), we have

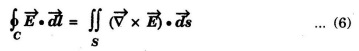
On substituting the eqn (6) in eqn (5), we get

Since this must be true for all surfaces S, it follows that

Eqn. (8) represents Maxwell's equation from Faraday's law of electromagnetic induction in differential form.

Statement:

The electromotive force around a closed path is equal to the rate of magnetic displacement (flux density) through that closed path.

Conduction current density

This is the current due to flow of electrons through the resistance in the circuit obeying ohm's law

We know that

where ρ - resistivity of the conductor

l - length of the conductor 

A - area of cross-section of conductor

σ - Conductivity of conductor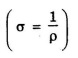

Substituting for R from eqn (2) in eqn (1), we have

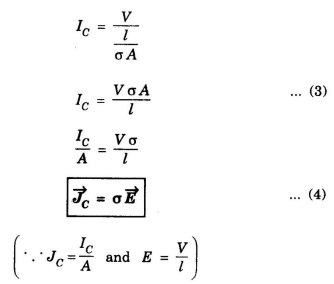
Here, Jc represents the conduction current density 

Displacement current density

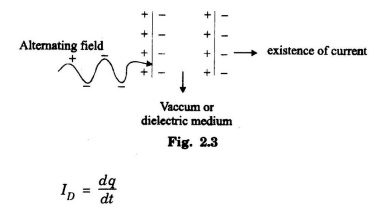
It is the current that exists across the capacitor in the circuit. When alternating field is applied to the parallel plate capacitor, no charge motion takes place (Fig 2.3).

It is due to vacuum or dielectric medium in capacitor but exchange (displacement) of charge takes place inside the capacitor.

It results in the existence of current on the surface of capacitor. This current is called displacement current in the capacitor.

But        q = CV

C- Capacitance of capacitor

V - Potential difference

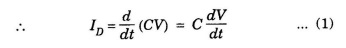
The capacitance of parallel plate capacitor is given by

where ε- Permittivity of the medium

A- Area of the parallel plate capacitor

d - Distance between two plates

Substituting for C from eqn (2) in eqn (1), we get

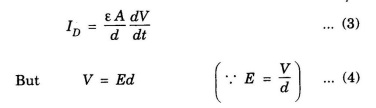
substituting eqn (4) in eqn (3), we have

Maxwell's Equation - IV

From Ampere's Circuital law

Ampere's law states that the line integral of magnetic field intensity H on any closed path is equal to the current (I) enclosed by that path

But, current density J = I/A

where A is cross sectional area

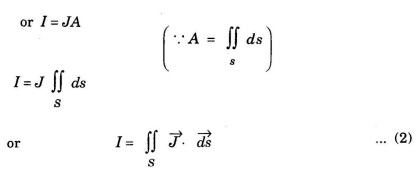
substituting eqn (2) in eqn (1), we have

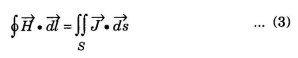
Ampere's law is modified by introducing displacement current density

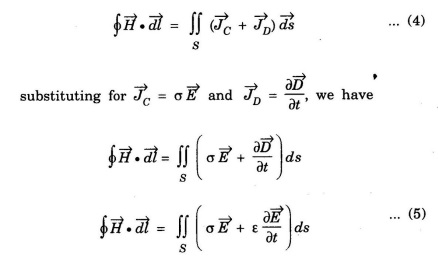
Unless or otherwise it is not specified, J stands for conduction current density alone. (ie., J = JC)

then,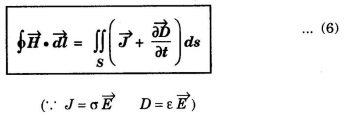  

This is Maxwell's equation in integral form from Ampere's circuital law.

Applying Stoke's Theorem to LHS of equation (6), we have

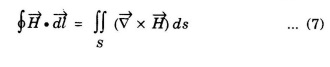
On substituting eqn (7) in ean (6) we get

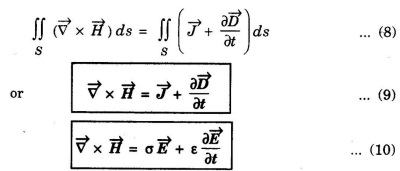
Equations (9) and (10) are Maxwell equations in differential form from Ampere's circuital law

Statement

The magnetomotive force around a closed path is equal to the sum of the conduction current and displacement current enclosed by the path.

Maxwell's equations are summarised as follows

Maxwell's Equations in Free Space

Four Maxwell's equations in differential form are

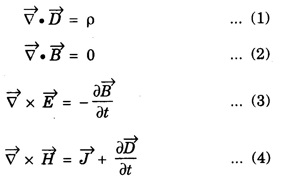
In a free space, there is no charges enclosed. There is no conductivity in the medium and conduction current is zero. Thus current density  and charge density ρ are zero. (ie., ρ = 0 and J = 0)

Therefore,

Maxwell's equations reduce to

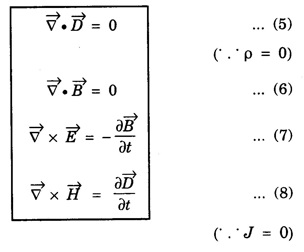
Maxwell's Equations in Conducting Media

In conducting media,

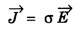 where σ is electrical conductivity of the conducting medium

where μ is permeability of the medium 

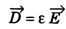where ε is the permittivity of the conducting medium

By applying above conditions, general Maxwell's equations reduce to

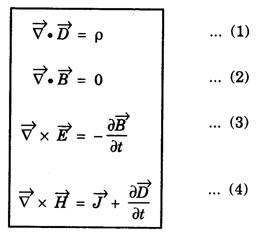
Characteristics of Maxwell's Equation 

1. Maxwell's First Equation;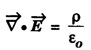

• It explains Gauss's law in electrostatics.

• It is time independent or steady state equation.

• The flux of the lines of electric force depends upon charge density.

• Charge acts as a source or sink for the lines of electric force.

2. Maxwell's Second Equation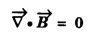

• It expresses a well known observation that isolated magnetic poles do not exist. 

• It states that total magnetic flux entering and leaving a given volume is equal. 

• There is no source or sink for lines of magnetic force. 

• It is a time independent equation.

• It explains Gauss's law in Magnetostatics.

3. Maxwell's Third Equation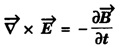

• It relates the electric field vector and magnetic induction vector

• It is a time dependent or time varying equation. 

• It explains the well known Faraday's laws and Lenz's law of electromagnetic induction.

• is generated by the time variation of

4. Maxwell's Fourth Equation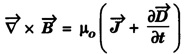

• It gives relation with the magnetic field vector with displacement vector and the current density  

• It is also a time dependent equation. 

• It explains Ampere's circuital law. 

• can be produced by and the time variation of  

Plane Wave

If a wave is confined to a particular plane (instead of in 3-dimensions) and propagating along particular axis with equal magnitudes of electric and magnetic field vectors, then that wave is called plane wave.