Lami's Theorem

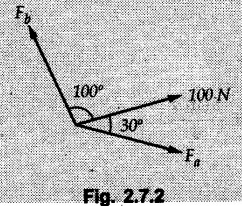
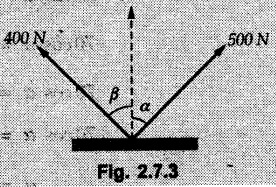
Lami's Theorem,

• It states that, "if three concurrent forces are in equilibrium, magnitude of any force is proportional to the sine of angle between the other two forces".

• For the three concurrent forces F1, F2 and F3 as shown in Fig. 2.7.1.

• Problems involving resolution of force into non perpendicular components can be solved using Lami's theorem.

• The problem is first converted into an equilibrium problem using concept of equilibrant and then solved using Lami's theorem as illustrated in the following two examples.

Solved Examples for Understanding

Example 2.7.1 

Find components Fa and Fb of the 100 N force along the directions shown in Fig. 2.7.2 using Lami's theorem.

Solution : 

• To use Lami's theorem, convert the problem to an equilibrium problem using equilibrant.

• The 100 N force shown has to be resultant of Fa and Fb.

⸫ A 100 N force in opposite direction (equilibrant) will be able to keep Fa and Fb in equilibrium as shown in Fig. 2.7.2 (a).

Using Lami's theorem,

Note: 

Equilibrant is same in magnitude as that of resultant but opposite in direction.

Example 2.7.2 

If the resultant of the two forces shown in Fig. 2.7.3 is 700 N directed bertically upwards, find the angles α and β using Lami's theorem.

Solution: 

• As the resultant is 700 N vertically upward, the equilibrant will be 700 N vertically downward as shown in Fig. 2.7.3 (a). 

• By Lami's theorem,

Squaring, we get,

16 - 25 sin2α = 49 - 70 cos α + 25 cos2 α

70 cos α = 49 + 25 cos2 α + 25 sin2 α - 16

⸫ 70 cos α = 49 + 25 – 16

70 cos α = 58

From equation (1),

4 sin β = 5 sin 34.05

β = 44.42°                 ... Ans.

Note: The solution by Lami's theorem becomes tedious when angles are unknown.