Engineering Graphics: Unit I (c): Conic Sections
Hyperbola
Engineering Graphics (EG)
Hyperbola is a curve traced out by a point moving in a plane such that the difference between its distances from two fixed points (called the foci), is a constant.
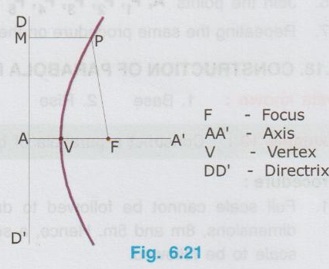
HYPERBOLA Hyperbola is a curve traced out by a point moving in a plane such that the difference between its distances from two fixed points (called the foci), is a constant. A hyperbola has two branches, two foci and two directrices as shown in Fig. 6.20. Sum of the distances of the point measured from two Foci ie., (F1P+ PF2) is known as length of Thread. It is also to be noted that (PF1 - PF2) = a constant, which is equal to the distance V1 - V2 ie., the distance between the vertices. A single branch of hyperbola is defined as the locus of a point P moving in a plane such that the ratio of its distance from a fixed point, called focus to the fixed straight AAA RO MOTOUR line, called Directrix is a constant and is always greater than unity. Eccentricity, e = Distance of the point from Focus / Distance of the point from Directrix = a constant > 1 Refering the Fig. 6.21, e = FP/PM For a single branch of hyperbola, definitions like Fig. 6.21 Focus, Directrix, Abscissa, Ordinate, Double ordinate, Latus to elsoa Rectum etc., are defined as explained for a parabola.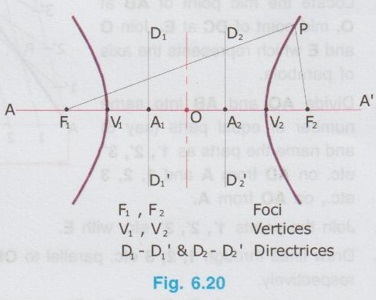
Engineering Graphics: Unit I (c): Conic Sections : Tag: : Engineering Graphics (EG) - Hyperbola
Engineering Graphics: Unit I (c): Conic Sections
Under Subject
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation