Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics
Hydrostatic law
Definition, Statement, Formula, Derivation
The pressure at any point in a fluid at rest is obtained by the Hydrostatic law which states that the rate of increase of pressure in a vertically downward direction must be equal to the specific weight of the fluid at that point.
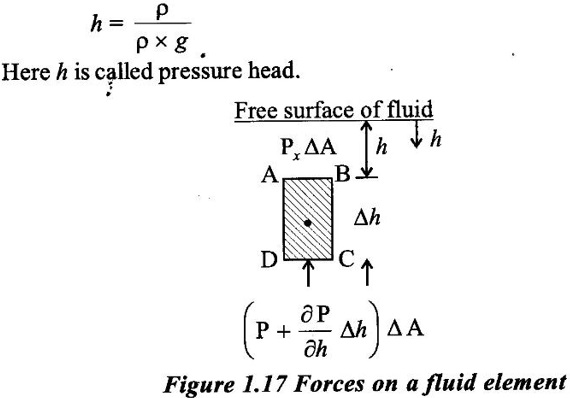
HYDROSTATIC LAW The pressure at any point in a fluid at rest is obtained by the Hydrostatic law which states that the rate of increase of pressure in a vertically downward direction must be equal to the specific weight of the fluid at that point. This is proved as: Consider a small fluid element as shown in fig 1.17. Let ΔA = cross-sectional area of element Δh = height of fluid element P = pressure on face AB h = distance of fluid element from free surface. The forces acting on the fluid element are: 1. Pressure force on AB = P × ΔA and acting perpendicular to face AB in the downward direction. 2. Pressure force on 3. Weight of fluid element = Density × g × volume = ρ × g × (ΔA × Δh) 4. Pressure forces on surfaces BC and AD are equal and opposite. For equilibrium of fluid element, we have Where w = weight density of fluid EQ states that rate of increase of pressure in a vertical direction is equal to weight density of the fluid at that point. This is Hrdrostatic law. By integrating the above eq for liquids ∫ dp = ∫ ρg dh P = ρ g h where P is the pressure above atmospheric pressure and h is the height of the point from free surfaces.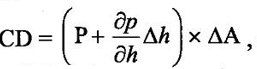
acting perpendicular to face CD, vertically upward direction.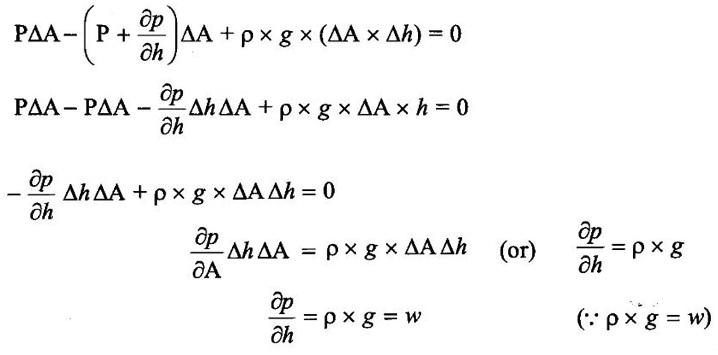
Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics : Tag: : Definition, Statement, Formula, Derivation - Hydrostatic law
Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics
Under Subject
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Fluid Mechanics and Machinery
CE25C02 3rd Semester CIVIL, AGRI Depts | 2025 Regulation | 3rd Semester 2025 Regulation
Fluid Mechanics and Machinery Laboratory
CE25C07 3rd Semester AGRI Dept 4th Semester CIVIL Dept | 2025 Regulation | 3rd, 4th Semester 2025 Regulation
Fluid Mechanics and Machinery
CE25C12 4th Semester Mechanical Department | 2025 Regulation | 4th Semester 2025 Regulation
Fluid Mechanics and Machinery Laboratory
CE25C07 4th Semester Civil Department | 2025 Regulation | 4th Semester 2025 Regulation
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Engineering Materials and Metallurgy
ME3392 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
Manufacturing Processes
ME3393 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation