Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics
Eulers equation of motion
Principle of Conservation of Energy [Fluid Flow]
The dynamic behavior of fluid motion is governed by a set of equations known as equations of motion.
EQUATIONS OF MOTION The dynamic behavior of fluid motion is governed by a set of equations known as equations of motion. These equations are obtained by using Newton's second law, which may be written as Fx = m.ax_where Fx is the net force acting in X direction up on a fluid element of mass m producing an acceleration ax in the X direction. In fluid flow, the following forces are present (i) Gravity force (Fg) (ii) Pressure force (Fp) (iii) Viscosity force (Fv) (iv) Turbulent force (Ft) (v) Compressibility force (Fc) Thus net force in X direction is Fx = (Fg)x + (Fg)x + (Fv)x + (Fc)x a. If the force due to compressibility (Fc) is neglected the resultant net force Fx = (Fg)x + (Fp)x + (Fv)x + (Ft)x The above equation is called as Reynolds equation of motion b. For flow, where Ft and Fc are negligible the resultant net force Fx = (Fg) x +(Fp) x + (Fv) x The above equation is called Navier stokes equations c. If the flow is assumed to be ideal, viscous force Fv is zero then the equation of motion is known as Eulers equation of motion and is given by Fx = (Fg) x + (Fp) x Consider steady flow of an ideal fluid along the stream tube. Let us consider a 'small element MN (differential control volume) from the stream tube in which dA be the cross sectional area and ds be the length as shown in figure1.23. P = pressure on the element at M P + dp = Pressure on the element at N V = velocity of the fluid element The external forces tending to accelerate the fluid element in the direction of stream line are as follows (i) Pressure force Pressure force on the element M = pdA Pressure force on the element N = (P + dP) × dA Net pressure force in the direction of flow = pdA - (P + dP) × dA = pdA – pdA – dPdA = dPdA (ii) Weight of the fluid element in the direction of flow Weight = mass × acceleration due to gravity = Density × volume × acceleration due to gravity Mass of the fluid element = ρ (dA × dS) According to Newtons law of motion, Force F = mass × acceleration Pressure force + Gravity force or weight of the element = mass × acceleration The above equation is called Euler's equation of motion. 1. Derivation of Bernoulli's equation from Euler's equation dP/ρ +VdV + gdZ = 0 Integrating the above equation Above equation divided by g The above equation is called Bernoulli'sequation for a steady flow of a friction less incompressible fluid along a stream line.Eulers equation of motion

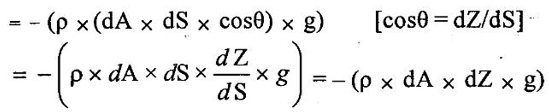 The negative sign indicates the weight of the component acting in the downward direction.
The negative sign indicates the weight of the component acting in the downward direction.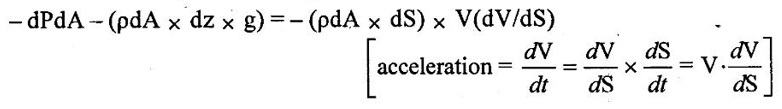 The above equation is divided by pdA on both sides
The above equation is divided by pdA on both sides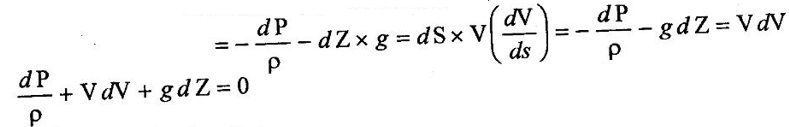
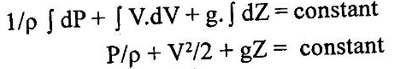
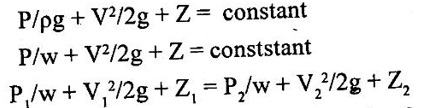
Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics : Tag: : Principle of Conservation of Energy [Fluid Flow] - Eulers equation of motion
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
