Engineering Physics: Unit II: Electromagnetic Waves
EM waves in conducting medium (medium with finite μ, ε and σ)
Electromagnetic Waves
This is the general wave equation for the electric vector in an electromagnetic wave propagating in conducting medium.
EM WAVES IN CONDUCTING MEDIUM (Medium with Finite μ, ε and σ) General Maxwell's equations are In conducting medium σ ≠ 0 i.e., there is a conduction current in the medium therefore Therefore the eqn. (1) reduces to or Here Taking the curl on both sides of eqn. (3), we get From vector calculus identity, we have But from eqn. Therefore, equation (7) becomes Substituting the eqn. (8) and (9) in (6), we get On substituting the value of Since This is the general wave equation for the electric vector in an electromagnetic wave propagating in conducting medium. In a similar way, by taking the curl of the eqn. (4) we obtain the general wave equation for the magnetic vector in a conducting medium as Wave Equation for Plane Polarized EM Waves Let us consider that the electromagnetic wave is travelling in the x-direction and the electric vector is directed along the y-axis and the magnetic vector is directed along the z-axis. For such a wave we have Therefore, the wave equations from (12) and (13), reduce to In the above wave equations Thus, the finite conductivity adds the diffusion term For vacuum or perfect insulators (σ = 0) and so these equations reduce to the expressions corresponding to the free space or dielectric medium. Solution of the plane Em Wave Equation in conducting medium (σ ≠ 0) The solution of the equation (14) should be a function of t and x and is of the form Similarly, the solution of the equation (15) is of the form Substituting eqn. (16) in egn. (14) For good conductors, we have σ >> ω ε. Therefore, μ ε ω2 can be neglected as compared to μ σ ω. Hence, from equation (18), we have Taking square root on both sides Taking the -ve value of y which gives the wave propagation in the +ve x-direction and substituting in the eqn. (16) we get This is a progressive wave having amplitude equal to In conducting medium the amplitude of the electromagnetic wave decreases exponentially with distance of penetration of the wave. Suppose, the amplitude at a depth x is denoted by Eox , then The decrease in the amplitude or the attenuation of the field vector is quantitatively expressed in terms of a quantity called skin depth. It is defined as the distance inside the conductor from the surface of the conductor at which the amplitude of the field vector is reduced to l/e times its value at the surface. According to Maxwell, an accelerated charge is a source of electromagnetic radiation. • In an electromagnetic wave, electric and magnetic field vectors are at right angles to each other and both are at right angles to the direction of propagation. They possess the wave character and propagate through free space without any material medium. These waves are transverse in nature. • Fig. 2.6 shows the variation of electric field 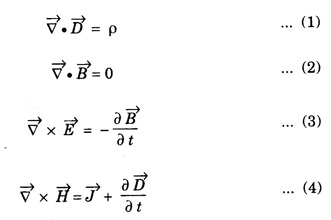
![]() but the charge density is zero everywhere (inside the conductor the charge density is always zero). That is ρ = 0.
but the charge density is zero everywhere (inside the conductor the charge density is always zero). That is ρ = 0.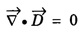
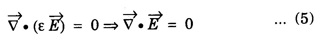
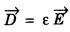 and ε is permittivity of the medium.
and ε is permittivity of the medium. 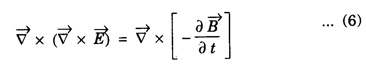
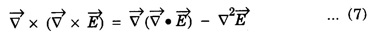

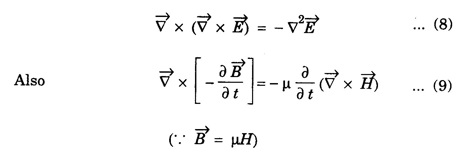
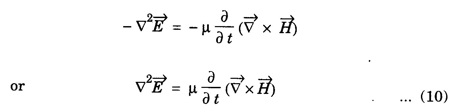
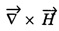 from eqn. (4) in eqn. (10), we have
from eqn. (4) in eqn. (10), we have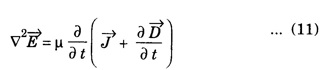
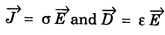 equation (11) becomes
equation (11) becomes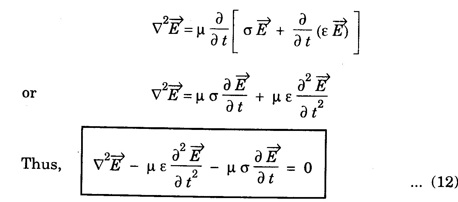
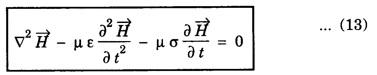
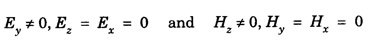
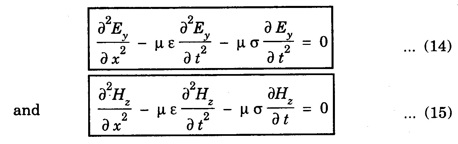
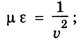 where v is the velocity of electromagnetic wave in conducting medium. The product μσ is called magnetic diffusivity.
where v is the velocity of electromagnetic wave in conducting medium. The product μσ is called magnetic diffusivity.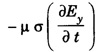 to the wave equation. This is due to the presence of conduction current
to the wave equation. This is due to the presence of conduction current 


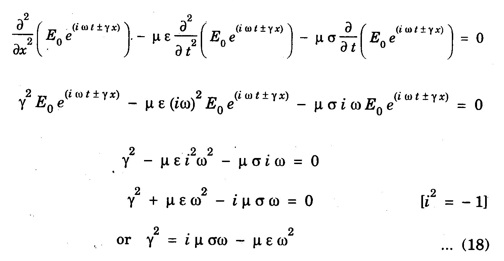
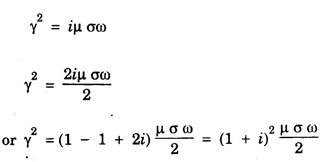
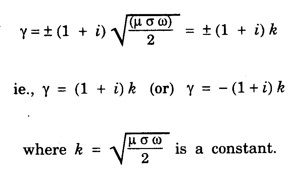
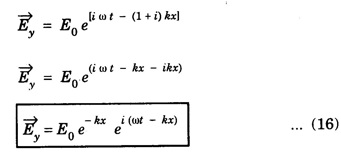
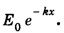 The amplitude of the wave goes on decreasing as the wave propagates deeper into the medium. Also the propagation constant k which is a constant depending upon the value of μ and σ.
The amplitude of the wave goes on decreasing as the wave propagates deeper into the medium. Also the propagation constant k which is a constant depending upon the value of μ and σ.Skin Depth (or) Penetration Depth
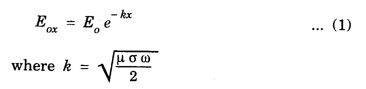
Electromagnetic waves
![]() along Y direction and magnetic field
along Y direction and magnetic field ![]() along Z direction and wave propagation in +X direction.
along Z direction and wave propagation in +X direction.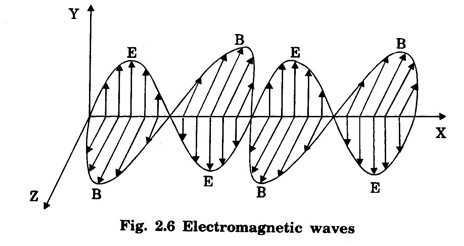
Engineering Physics: Unit II: Electromagnetic Waves : Tag: : Electromagnetic Waves - EM waves in conducting medium (medium with finite μ, ε and σ)
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
