Engineering Physics: Unit II: Electromagnetic Waves
Electromagnetic Energy flow and Poynting Vector
Electromagnetic Waves
Electromagnetic waves transports energy from one region to another.
ELECTROMAGNETIC ENERGY FLOW AND POYNTING VECTOR Electromagnetic waves transports energy from one region to another. This energy transferred is described by power / unit area for an area perpendicular to the direction of an EM wave travel. Let us consider a stationary plane perpendicular to the x-axis which coincides with the wave front at a certain time t. (Fig 2.19) At a time Δt after this, the wavefront moves a distance to the right side of the plane. Area of cross section of the stationary plane is A and its volume ΔV = A· Δ x = A·c. Δ t. If Δ U is the available energy in this volume, then then Here 'u' is the energy density which is equal to ε0 E2. This energy ΔU passes through the area 'A' in time Δt. Therefore, the energy flow / unit time / unit area is Since E = c B and Eqn. (2) becomes The unit of 'S' is energy per unit area per unit time or power per unit area. The SI unit of 'S' is W/m2. In vector quantity, it is represented as Eqn. (6) is the Poynting vector in vacuum. Its direction is in the direction of the propagation of the EM wave.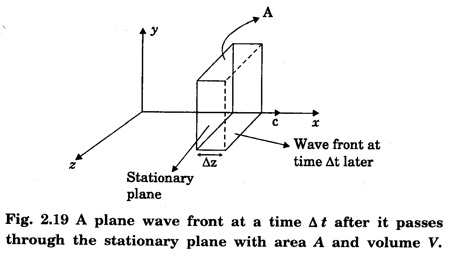

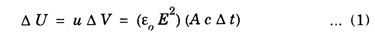

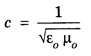

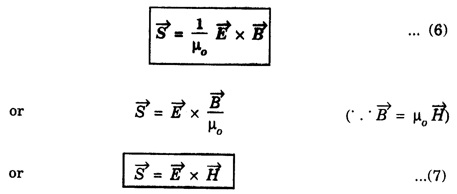
Engineering Physics: Unit II: Electromagnetic Waves : Tag: : Electromagnetic Waves - Electromagnetic Energy flow and Poynting Vector
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
