Engineering Physics: Unit III: c. Lasers
Einstein's A and B Coefficients (Derivation)
Lasers
Consider an assembly of atoms with different energy states at an absolute temperature T.
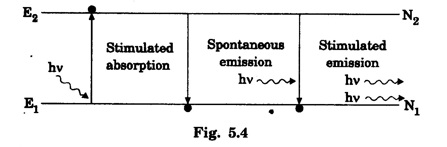
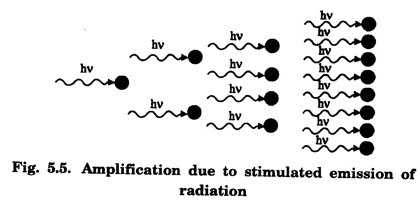
EINSTEIN'S A and B COEFFICIENTS (Derivation) Consider an assembly of atoms with different energy states at an absolute temperature T. When light radiation is incident on these atoms, three different processes take place. They are (a) stimulated absorption (b) spontaneous emission (c) stimulated emission The atom in the lower energy state E1 absorbs radiation and is excited to the higher energy level E2. This process is called stimulated or induced absorption (Fig. 5.4). The rate of stimulated absorption is directly proportional to number of atoms (N1) in energy state E1 and the energy density (Q) of incident radiation (number of photons incident per unit area per unit time). Therefore, the number of stimulated absorption transitions occuring per unit time is given by where B12 is a proportionality constant. This process is an upward transition. (Fig 5.4) The atoms in excited state return to lower energy state E1 (ground state) by emitting a photon of energy hv in two ways. (a) Spontaneous emission (b) Stimulated emission The atoms in the excited state E2 return to lower energy state E1 by emitting a photon of energy hv without the influence of any external agency. This emission of light radiation is known spontaneous emission. (Fig. 5.4) The rate of spontaneous emission is directly proportional to the number of atoms in the excited energy state (N2). Hence, the number of transitions per second is given by Here, Ag, is a proportionality constant. This process is a downward transition. (Fig. 5.4) If the light photon is incident on the atom in the excited energy state, the photon triggers the excited atom to make transition to lower energy E1 along with emission of photons. This kind of emission of light radiation is stimulated emission. (Fig. 5.4) The rate of transition is directly proportional to the number of atoms in the upper energy level (N2) and the energy density of incident radiation (Q). The number of transitions per second. where B12 is a proportionality constant. This process is also a downward transition. The proportionality constants A21, B12 and B21 are known as Einstein's coefficients A and B. Under equilibrium condition, the number of downward and upward transitions per second are equal. i.e., Nsp + Nst = Nab ... (4) Substituting from the eqns (1), (2) and (3), in eqn (4), we Rearranging the eqn (5), we have Dividing numerator and denominator by B12 N2, we have On substituting Planck's radiation formula for energy distribution is given by Comparing the eqns (8) and (9), we have Since B12 = B12, Einstein's coefficients are termed as A and B coefficients. ● The spontaneous emission is more predominant than the stimulated emission. The laser light is due to stimulated emission. Therefore, stimulated emission should be greater than spontaneous emission. To achive this, population inversion is required. ● The equation (11) gives the relation between spontaneous emission and stimulated emission coefficients. Since this ratio is proportional to v3, the probability of spontaneous emission increases with the energy difference between the two states. Note: The students are not expected to write the informations given in the box in the examination. The photon emitted during stimulated emission has the same energy, phase, frequency and direction as that of the incident photon. Thus, we have two coherent photons. Now, these two photons get incident on two other atoms in the state E2. This results in induced emission of two more photons. Now, there are four coherent photons of same energy. These four photons induce further transitions with four other atoms in the energy state E2. This gives stimulated emission of eight coherent photons of same energy (Fig. 5.5). If the process continues in a chain, ultimately, this gives rise to increase in intensity of coherent radiation enormously. Stimulated emission is multiplied through a chain reaction. This multiplication of photons through stimulated emission leads to coherent, powerful, monochromatic, collimated beam of light. This light is known as laser light. Thus for laser action, stimulated emission is most important. It is achieved by population inversion.Stimulated absorption
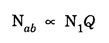

Spontaneous emission
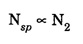

Stimulated emission
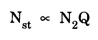

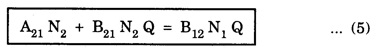
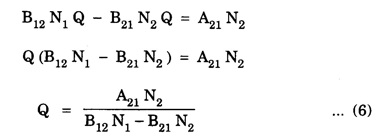
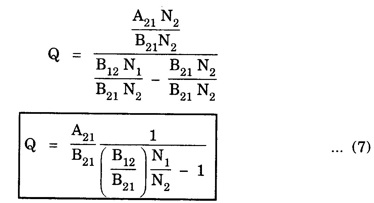
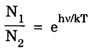 (from Boltzmann distribution equation) in eqn (7), we have
(from Boltzmann distribution equation) in eqn (7), we have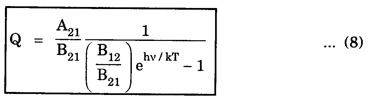
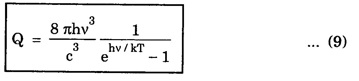
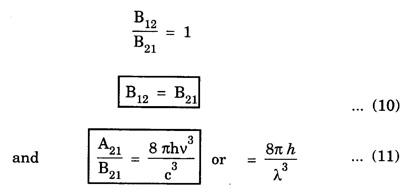
Conclusion

Concept of Laser
Engineering Physics: Unit III: c. Lasers : Tag: : Lasers - Einstein's A and B Coefficients (Derivation)
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
