cycloidal follower motion

CYCLOIDAL FOLLOWER MOTION

• In this case, as its name suggests, the displacement diagram of the follower is generated from a cycloid.

• We know that cycloid is a locus of a point on a circle rolling on a straight line.

• In case of cams, this straight line is the lift of the follower (L) and the circumference of the rolling circle is equal to the lift of the follower. The radius of the circle will be L/2π.

• The cycloidal curve is considered the best of all cam contours, as it has the lowest vibration, surface wear, contact stress, noise, and shock.

• Thus the cycloidal motion is recommended for follower when cam rotates even at higher speeds (i.e., it can be used for low, medium or higher speeds).

1. Construction of Displacement Diagram

The displacement diagram when the follower moves with cycloidal motion is shown in Fig.3.20.

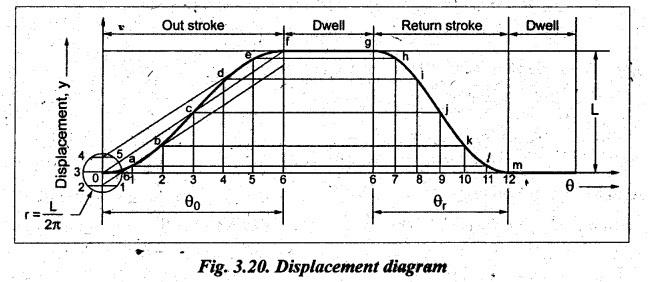
The displacement diagram can be constructed as follows:

Step 1: Divide the angular displacement of the cam outstroke into any even number of equal parts (say 6) and draw vertical lines through these points.

Step 2: Draw diagonal line ‘0ƒ”.

Step 3: Draw circle with centre 0 with radius equal to (L/2π).

Step 4: Divide the circle into same number of equal parts (say 6) as cam displacement is divided.

Step 5: Project the points on the circles to its vertical diameter and these points on the diameter are projected parallel to the diagonal (0f) to the corresponding vertical lines 1, 2, 3, 4, 5 and 6. Now obtain the intersection points a, b, c, d, e and f.

Step 6: Join these intersection points to obtain the cycloidal displacement curve for the outstroke of the follower.

Step 7: Follow the same procedure to draw the displacement curve for the return stroke of the follower.

2. Determination of Displacement, Velocity, Acceleration and Jerk of Follower having Cycloidal Motion

1. Displacement of the Follower

Mathematically, the displacement equation for the follower having cycloidal motion during outstroke is given by

where

y_o = Displacement of the follower during outstroke after any time i,

L= Lift (or stroke) of the follower,

θ = Angle through which the cam rotates in time t, and

θ_o = Outward angle (or angle of ascent).

Similarly, the displacement of follower during return stroke,

where

θ_r = Return angle (or angle of descent)

(ii) Velocity of the Follower

We know that, Velocity = Rate of change of displacement with respect to time

v = dy/dt

Velocity of follower during outstroke is given by

Maximum velocity of follower during outward and return strokes

(iii) Acceleration of the Follower

We know that, Acceleration = Rate of change of velocity with respect to time

a = dv/ dt

Acceleration of follower during outstroke is given by

Maximum acceleration of follower during outward and return strokes

(iv) Jerk of the Follower

We know that,

Jerk = Rate of change of acceleration with respect to time

j = da / dt

Jerk of follower during outward stroke is given by

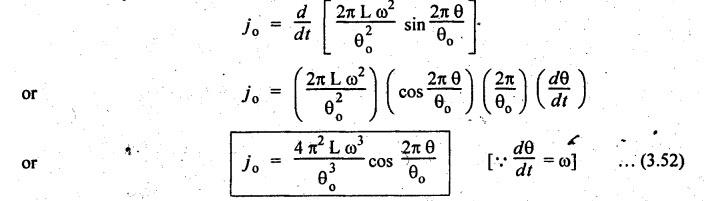
Similarly, jerk of follower during return stroke is given by

Maximum jerk of follower during outward and return strokes

Similarly, the maximum jerk of follower during return stroke occurs when θ = 0° and θ = θ_r and is given by

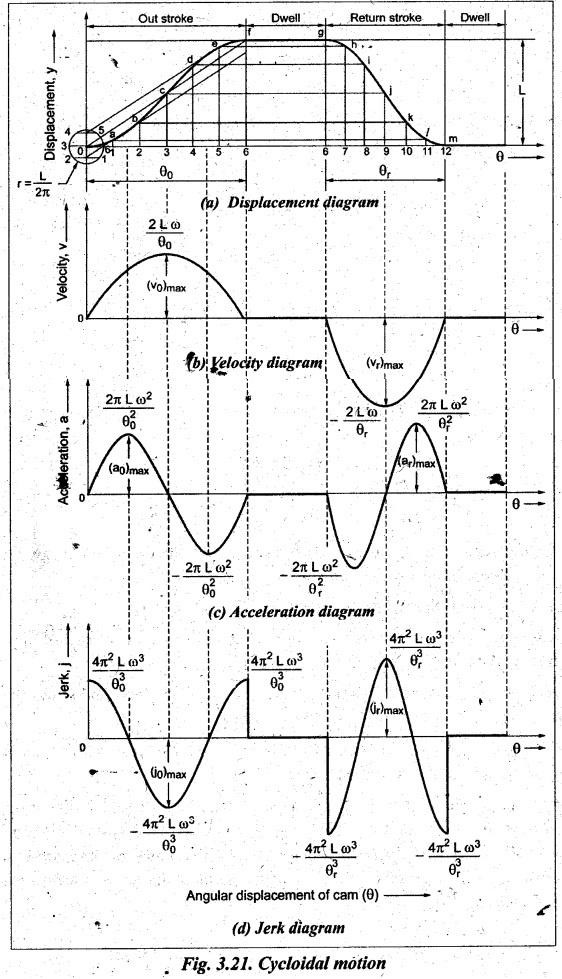
• Fig.3.21 illustrates the displacement, velocity, acceleration and jerk diagrams when the follower moves with cycloidal motion.

• From Fig.3.21, the following points may be observed:

■ The velocity of the follower is zero at the beginning and at the end of its strokes and increases gradually to a maximum at mid-stroke.

■ The acceleration of the follower is zero at the beginning, mid and at the end of stroke and is maximum at 1/4th and 3/4th of each stroke.

■ The jerk of the follower is zero at 1/4th and 3/4th of its stroke and is maximum at the beginning, mid and at the end of stroke.

■ Since the acceleration curve is continuous and the value of jerk is not infinite anywhere, therefore the cycloidal curve is considered the best of all cam contours. Hence the cams with cycloidal motion for followers are recommended for higher speeds, (i.e., this type of follower motion is suitable for lower, moderate and higher speed applications).