Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics
Continuity Equation in One Dimensional
Principle of Conservation of Energy [Fluid Flow]
The continuity equation based on the principle of conservation of mass which states that the mass of fluid entering the pipe from one end must be equal to the mass of fluid leaving the pipe at other end per unit time, if no fluid is added or removed from the pipe.
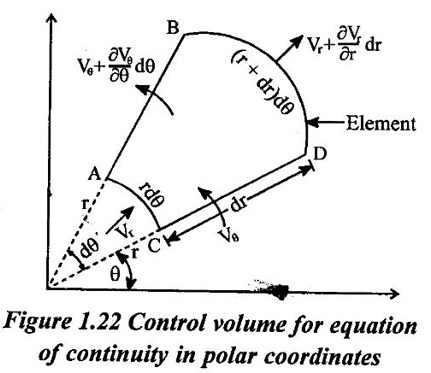
CONTINUITY EQUATION IN ONE DIMENSIONAL The continuity equation based on the principle of conservation of mass which states that the mass of fluid entering the pipe from one end must be equal to the mass of fluid leaving the pipe at other end per unit time, if no fluid is added or removed from the pipe. The continuity equation can be derived based on pipe with the following assumptions (i) Steady flow (ii) Uniform flow (iii) Incompressible flow (iv) One dimensional flow Consider two cross section of a pipe as shown in figure 1.20 Let A1 arça of the pipe at section 1–1 V1 = velocity of the pipe at the section 1-1 ρ1 = density of the fluid at section 1-1 A2, V2, ρ2 are the corresponding values at section 2-2 The total quantity of fluid or mass flow rate of fluid passing through a section 1-1 = Density × Volume = ρ1 × A1 × V1 & the total quantity of fluid passing through a section 2-2 = ρ2 × A2 × V2 By law of conservation of mass, we have ρ1 × A1 × V1 = ρ2 × A2 × V2 The above equation is called continuity equation and is applicable to only the compressible fluids. For incompressible fluids ρ1 = ρ2 Therefore the above equation is reduced to A1V1 = A2V2 The product AV is the quantity of fluid is called as flow rate or discharge (Q). The mass flow rate of fluid (ρ AV) is expressed in Kg/sec. 1. Continuity equation in Cartesian coordinates or rectangular coordinates Consider a fluid element (differential control volume) separate from the large fluid element, parallelepiped with sides dx, dy and dz as shown in figure.1.21 ρ = Mass density of the fluid at a particular instant. u,v,w = components of velocity of flow in X, Y and Z directions respectively. Rate of mass of fluid entering the face ABCD in X direction = Density × Velocity × Area = ρ × u × dy dz Rate of mass of fluid leaving from the face EFGH in X direction = mass of fluid entering the face ABCD + rate of increase of mass of fluid leaving the element in X direction = ρ × u × dy dz + ə/əx (ρ × u × dy dz) dx The gain of mass in the X direction per unit time due to flow in the X direction is given by the difference between the fluid entering and leaving = entering the mass in X direction - leaving the mass of fluid in X direction = (ρ × u × dy dz) – [ρ × u × dy dz + ə/əx (ρ × u × dy dz) dx] = - ə/əx × (ρ × u × dy dz) dx = - ə/əx × (ρ × u) dx dy dz [dxdydz is constant] Similarly, the gain in fluid mass per unit time in the parallelopiped due to flow in Y and Z directions = - ə/əy (ρ × v) dx dy dz = - ə/əz (ρ × w) dx dy dz The total or net gain in fluid mass per unit time for fluid along three co-ordinate axes = -{ ə/əx × (ρ × u) + ə/əy (ρ × v) + ə/əz (ρ × w) dx dy dz Rate of change of mass of the parallelopiped (differential control volume) = ə/ət × (ρ × dx dy dz) By law of conservation of mass total gain in fluid mass per unit time for fluid along three coordinates = rate of change of the mass of the parallelepiped -{ ə/əx × (ρ × u) + ə/əy (ρ × v) + ə/əz (ρ × w) dx dy dz = ə/ət × (ρ × dx dy dz) There is no accumulation of mass and hence the above quantity must be equal to zero. ə/ət × (ρ × dx dy dz) + { ə/əx × (ρ × u) + ə/əy (ρ × v) + ə/əz (ρ × w) dx dy dz = 0 ə/ət × (ρ) + {{ ə/əx × (ρ × u) + ə/əy (ρ × v) + ə/əz (ρ × w) } = 0 The above equation is called general three dimensional continuity equations and is applicable to any type of flow and also for any fluid whether compressible or incompressible. For incompressible fluids, p = 0, the above equation reduces to {ə u / ə x + ə v/ ə y + ə w / ə z} = 0 For two dimensional flow the component w = 0 and hence the equation reduces to {ə u / ə x + ə v/ ə y} = 0 2. Continuity equation in polar or cylindrical coordinates: Consider a fluid element (differential control volume) - segment of a hollow cylinder shown in figure 1.22. The side of the element has the following dimensions. Sides AB = CD = dr Sides AC = rdθ and BD = (r + dr)dθ Vr = component of the velocity in radial direction Vθ = component of the velocity in tangential direction The thickness of the element perpendicular to the plane of paper is to be unity. Hence only the flows in radial and tangential direction are considered. Flow in radial direction Mass of fluid entering in radial direction (face AC) during time dt is given by = (density × rate of flow) × time = (density × velocity × area) × time = {ρ(Vr × r dθ)}dt Mass of fluid leaving in radial direction (face BD) during time dt is given by Neglecting the term dr2 The gain in mass per dt time due to flow in the radial direction is given by the difference between entering and leaving mass of fluid = Entering mass of fluid - Leaving mass of fluid Flow in tangential direction: Mass of fluid entering in tangential direction (face CD) during the time dt is given by = (density × velocity × area) × time = (ρ × Vθ × dr) × dt Mass of fluid leaving in tangential direction (face AB) during the time dt is given by = (density × velocity × area) × time The gain in mass per dt time due to flow in the tangential direction is given by the difference between mass of entering and leaving the fluid = mass of Entering fluid- mass of Leaving fluid. As per law of conservation of mass The total gain in mass in both radial and tangential direction = the rate of change of fluid mass in the element ABCD There is no accumulation of mass and hence the above quantity must be equal to zero.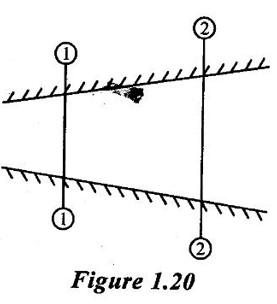

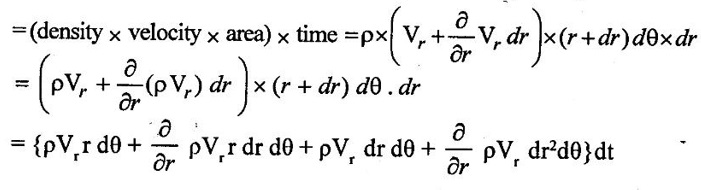
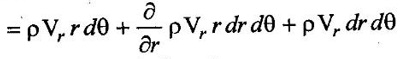
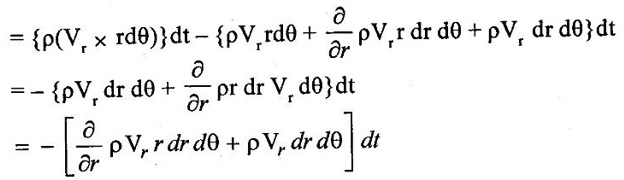

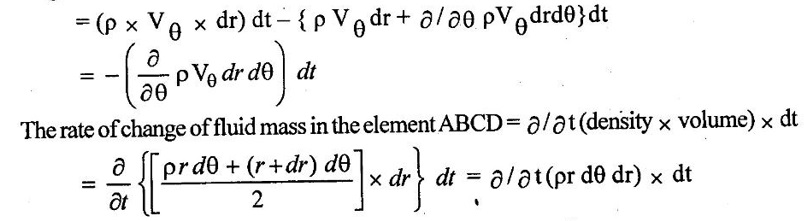


Fluid Mechanics and Machinery: Unit 1: Fluid Properties and Flow Characteristics : Tag: : Principle of Conservation of Energy [Fluid Flow] - Continuity Equation in One Dimensional
Related Topics
Related Subjects
Fluid Mechanics and Machinery
CE3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
