Engineering Graphics: Unit I (a): Geometrical Construction
Construction of Regular Polygons
Engineering Graphics (EG)
Any plane figure bounded by more than four straight lines is called a polygon.
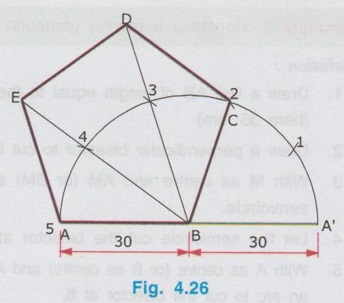
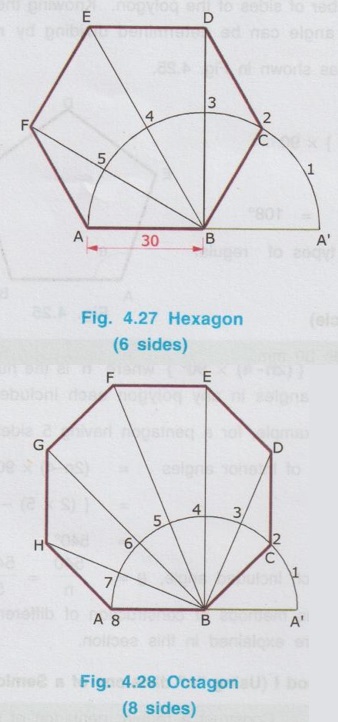
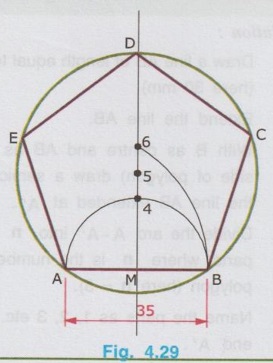
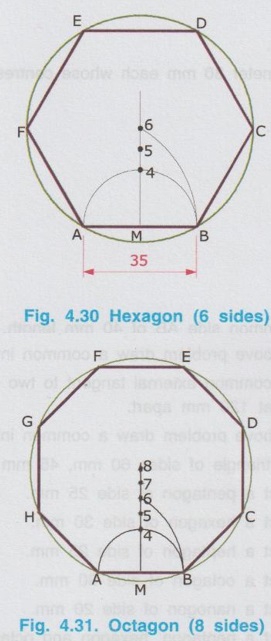
CONSTRUCTION OF REGULAR POLYGONS Any plane figure bounded by more than four straight lines is called a polygon. A polygon having equal sides and equal angles is called a Regular Polygon. Various types of polygons are explained in article 4.3 (Sl. No. 6). The straight lines that make up the regular polygon are called its sides and the points where the sides meet are called the vertices. The important geometric property of any polygon is the sum of interior angles in any polygon is equal to {(2n- 4) × 90° } where `n' is the number of sides of the polygon. Knowing the sum of interior angles in any polygon each included angle can be determined dividing by n. For example, for a pentagon having 5 sides as shown in Fig. 4.25. Sum of Interior angles = (2n - 4) × 90 = {(2 × 5) – 4 } × 90 = 540° ⸫ Each included angle, θ = 540/n = 540/5 = 108° Various methods of construction of different types of regular polygons are explained in this section. 1. Method I (Using "n" divisions of a Semicircle) Example 1 : Construct a regular pentagon of side 30 mm. Solution : 1. Draw a line AB of length equal to side of polygon. (here 30 mm) 2. Extend the line AB. 3. With B as centre and AB as radius (equal to side of polygon) draw a semicircular arc to cut the line AB extended at A'. 4. Divide the arc A - A' into n number of equal parts, where n is the number of sides of the polygon (here n = 5). 5. Name the parts as 1, 2, 3 etc. starting from the end A'. 6. Join B and 2 and note the point 2 as C. 7. Similarly Join the points 3 and 4 with B and extend. 8. With 2 as centre and radius equal to the side of polygon (here 30 mm) draw an arc to cut the line B3 produced at D. 9. similarly with D as centre and radius equal to the side of polygon (ie., 30 mm) draw an arc to cut the line B4 extended at E. 10. Join the points C, D, E and A to get the required pentagon ABCDE. Note : i) Divide the semi-circle into `n' number of divisions, where `n' is the number of sides of polygon and name the parts from A'. ii) But for any type of polygon always join the second division (Point number 2) from A'. iii) The method described above example can be followed to draw any polygon. Hexagon and Octagon drawn in this method are given below for comparison. 2. Method II : (Using Perpendicular Bisector) Example 2: Construct a regular pentagon of side 35 mm. Solution : 1. Draw a line AB of length equal to the side of polygon (here 35 mm) 2. Draw a perpendicular bisector to cut the line AB at M. 3. With M as centre and AM (or BM) as radius draw a semicircle. 4. Let the semicircle cut the bisector at 4. 5. With A as centre (or B as centre) and AB as radius draw an arc to cut the bisector at 6. 6. Locate the midpoint of the distance 4 to 6 at 5. 7. With Point 5 (the number which is equal to the number of sides) as centre and 5A (or 5B) as radius draw a circle which will pass through the points A and B. 8. Mark off the sides of the pentagon on the circle by cutting arcs with radius equal to AB. (ie., With B as centre draw an arc of radius equal to the side of pentagon to cut the circle at C. Then with C as centre and the same radius draw an arc to cut the circle at D and so on). 9. Name the divisions as C, D and E. 10. Join the points A, B, C, D and E with straight lines which is the required pentagon. Note : i) The above method can be followed to draw any polygon. ii) For any polygon always take the point of intersection of semicircle with bisector as 4 and the point of intersection of arc with bisector as 6 and then locate the midpoint of the distance 4 to 6 as 5. iii) After locating the point 5, take the distance 4 to 5 in a divider and mark it on the perpendicular bisector to mark the succeeding points 7, 8, 9 etc. such that the distances 4-5 = 5 – 6 = 6 - 7 = 7 - 8 etc. iv) Draw a circle taking the point 5 as centre for pentagon, point 6 as centre for hexagon, point 7 as centre for heptagon etc., and radius equal to the length measured from that point to A (or B). v) Finally mark off the required number of sides of the polygon on the circle by cutting arcs with radius equal to the side of polygon. Hexagon and Octagon drawn in this method are given below for comparison. Example 3 : Draw Pentagon, Hexagon and Octagon of side 40mm on a common base side. Solution : 1. Draw a line AB of 40mm length. 2. Draw bisector of AB and draw an arc with A as centre and AB as radius. 3. Mark the points 4 and 6 on the bisector and locate the mid point of 4-6 as 5. 4. Taking the point 5 as centre draw a circle with radius 5-A and mark off the vertices C, D and E on the circumference of circle. 5. Similarly draw Hexagon and Octagon taking the points 6 and 8 as centres and 6-A and 8-B as radius respectively. Mark off the vertices and join by straight lines.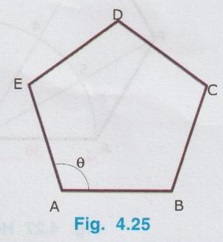

Engineering Graphics: Unit I (a): Geometrical Construction : Tag: : Engineering Graphics (EG) - Construction of Regular Polygons
Related Topics
Related Subjects
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
