Construction of Hyperbola by Eccentricity Method

CONSTRUCTION OF HYPERBOLA BY ECCENTRICITY METHOD

Data known: 

1. Distance of the Focus from Directrix,

2. Eccentricity.

Points to understand

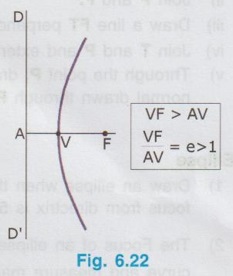
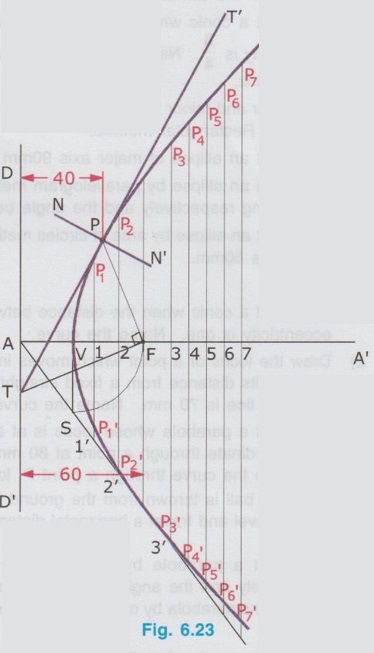
1. Hyperbola is a open and indefinite curve.

2. Eccentricity of hyperbola is greater than one and hence the distance of vertex from Focus is more than the distance from Directrix.

3. For the construction of hyperbola, steps followed for the construction of parabola can be followed.

Example 11: Construct a Hyperbola if the distance between the focus and directrix is 60 mm and eccentricity is 3/2. Also draw the tangent and normal at a point at 40 mm from the directrix.

Construction: 

1. Draw Directrix DD'.

2. Locate the point A on DD' and draw principal axis AA', perpendicular to the directrix DD'. 

3. Mark Focus F at a distance of 60 mm (given distance) from the Directrix on the major axis. ie., AF = 60 mm.

4. Eccentricity is given as 3/2. So divide the line AF into 5 parts (3 + 2 = 5) and mark vertex V on AF such that VF/AV = 3/2.

5. Erect perpendicular through V and taking V as centre and VF as radius draw an arc to the cut the perpendicular drawn through V at S. 

6. Join A and S and extend.

7. Along the major axis AA' mark the points 1, 2, 3,.... etc. from V at approximately equal intervals.

8. Erect perpendiculars through the points 1, 2, 3,..... etc. to intersect the line AS extended respectively at 1', 2', 3'..... etc. 

9. With Focus F as centre and 1 - 1' as radius draw two arcs on either side of the axis to intersect the vertical line drawn through 1 at P1 and P1'.

10. Similarly with F as centre and 2 - 2, 3 - 3'.... etc. as radii draw arcs on either side of the axis to intersect the vertical lines drawn through the points 2, 3, ... etc. at P2 and P2', P3 and P3'.... etc. 

11. Join the points .... P3', P2', P1', V, P1, P2, P3…. etc. to form a smooth hyperbola curve.

To draw tangent and normal

i) Mark a point P on the hyperbola at 40 mm (given distance) from the directrix. 

ii) Join P and F.

iii) Draw a line FT perpendicular to the line PF through the Focus F to cut the directrix at T. 

iv) Join T and P and extend, which is the required tangent, TT'.

v) Through the point P, draw a line NN' perpendicular to the tangent TT', which is the required normal drawn through P.