Construction of Ellipse by Eccentricity Method

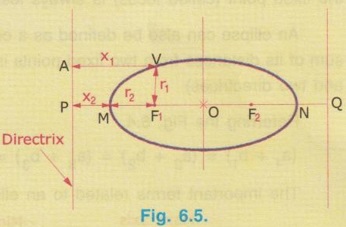
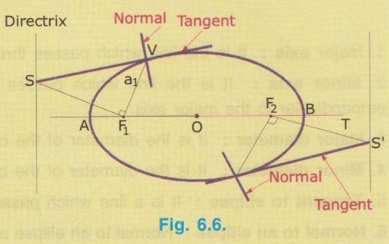
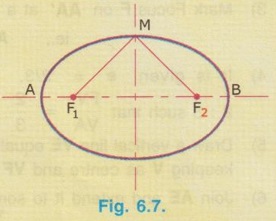
CONSTRUCTION OF ELLIPSE BY ECCENTRICITY METHOD

Data known :

1) Eccentricity of the ellipse

2) Distance of the Focus from the Directrix. 

Points to understand:

Understanding of following points will be very much useful to construct an ellipse by eccentricity method. 

1) Sum of distances of any point on the curve from focus and directrix is the same.

ie., (r1 + x1) = (r2 + x2)

2) Ellipse has two directrices and two Foci and hence, the distance of Foci from directrix and the distance of vertex of ellipse will be the same on either side. 

ie., PM = NQ and MF1 = NF2

3) eccentricity, e = Distance of the point on curve from Focus / Distance of the point on curve from Directrix

ie., e for the point V = r1/x1

Similarly e for the point M = r2/x2

Hence it is clear that the vertex of ellipse (ie., the point M) divides the line joining the points PF internally in the ratio x2 : r2.

4) When a perpendicular is erected through any point on the major axis of the ellipse, the ordinates on either side will be equal.

5) When a tangent is drawn through any point on the curve, the line joining that point and Focus will make an angle of 90° (right angle) with the line joining the Focus and the point of intersection of tangent with Directrix as shown in Fig.

6) Normal drawn through any point on curve will be right angleb (90°) to the tangent drawn through the same point.

7) Length of line joining the points Focus and Vertex of minor

axis is equal to (1/2 × Major axis)

ie., MF1 = MF2 = 1/2 × Major axis AB

or

MF1 + MF2 = Major axis AB

Hence if the major axis AB and Foci points F1 and F2 are known, minor axis can be easily located.

Example 1: Construct an ellipse when the distance of its focus from its directrix is 50 mm and eccentricity is 2/3. Also draw a tangent and normal to this ellipse at a point 80 mm away from the directrix.

Procedure:

1) Draw a vertical line DD', directrix of the ellipse.

2) Mark a point A on directrix and draw a line AA', perpendicular to the directrix, which represents the major axis.

3) Mark Focus F on AA' at a distance 50 mm (given in problem) from the directrix DD'. 

ie., AF = 50 mm

4) It is given e = 2/3, Hence divide the AF into two parts at V in the ratio of 2:3 such that FV/VA = 2/3.

5) Draw a vertical line VE equal to VF. For this, erect a perpendicular through V and draw an arc keeping V as centre and VF as radius to intersect the perpendicular at E.

6) Join AE and extend it to some distance. This line is called as eccentricity line. clearly in the right angled triangle AVE, VE/AV = 2/3 = eccentricity. 

(ie., AE produced) at (VE = VF)

7) Join F and E.

8) Draw a line through F at an angle of 45° to intersect the eccentricity line (ie., AE produced) at U. Clearly this line is perpendicular to the line FE since ∠EFV = 45° (VE = VF)

9) Erect a perpendicular through U to intersect the major axis AA' at V'. VV' = major diameter. 

10) Along the major axis AA' and from the point V mark the points 1, 2, .... at approximately equal intervals (need not be equal) and draw perpendiculars through these points to intersect the eccentricity line at 1', 2'..... respectively.

clearly, 1 - 1' / A – 1 = 2 - 2' / A – 2 =  eccentricity = 2/3

11) With Focus F as centre and 1 - 1' as radius draw two arcs on either side of the axis to intersect the vertical line drawn through 1 at P1 and P1'.

12) With Focus F as centre and 2 - 2' as radius draw two arcs on either side of the axis to intersect the vertical line drawn through 2 at P2 and P2' 

13) Repeat the steps 11 and 12 for points 3, 4.... etc. and obtain the points P3 and P3', P4 and P4 and P4' … etc.

14) Draw a smooth ellipse by free hand passing through the points V, P1, P2 …, V', …, P2', P1', V.

To draw Tangent and Normal at any point on ellipse

i) Mark a point P on the ellipse at the given distance 80 mm from the directrix.

ii) Joint P and Focus F.

iii) Draw a line FT perpendicular to PF meeting directrix at T.

iv) Join TP and extend, which is the required tangent, TT'

v) Through the point P draw a line NN' perpendicular to the tangent TP, which is the normal at P. 

To draw another Directrix

Mark A' on major axis such that V'A' = AV and draw perpendicular through A'. (Not shown in figure)

To Locate another Focus F'

Mark F on major axis such that V'F' = VF.

To draw Minor axis

i) Locate the mid point of major axis V-V′ at O.

ii) Erect perpendicular through O to intersect the ellipse at S and S' which is the minor axis of ellipse.

To Check

Check that FS = SF' = Major diameter V-V' / 2