Engineering Graphics: Unit I (c): Conic Sections
Conics - Important Definitions
Engineering Graphics (EG)
Mathematically, Conic is defined as the locus of a point moving in a plane in such a way that the ratio of its distance from a fixed point to a fixed straight line is always constant.
CONICS - IMPORTANT DEFINITIONS Mathematically, Conic is defined as the locus of a point moving in a plane in such a way that the ratio of its distance from a fixed point to a fixed straight line is always constant. The fixed point is known as 'Focus' and the fixed line is known as `Directrix' showndo in Fig. 6.2. The ratio of distance of the moving point from focus to the distance from directrix is known as eccentricity, represented by the do nollee ol letter 'e'. In fig. 6.2, r1, r2 and r3 are the distances of moving point from focus and X1, X2 and X3 are the distances of moving point from directrix. ⸫ Eccentricity, e = Distance of the moving point from Focus / Distance of the moving point from the Directrix Mathematically, the conic sections can be classified according to the value of eccentricity. If eccentricity, e < 1, the curve obtained is Ellipse. If eccentricity, e = 1, the curve obtained is Parabola. If eccentricity, e > 1, the curve obtained is Hyperbola. Ellipse, Parabola and Hyperbola are graphically represented by their eccentricity as shown in Fig. 6.3.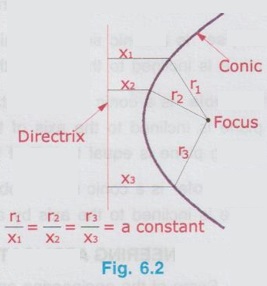
Engineering Graphics: Unit I (c): Conic Sections : Tag: : Engineering Graphics (EG) - Conics - Important Definitions
Engineering Graphics: Unit I (c): Conic Sections
Under Subject
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation