Engineering Physics: Unit II: Electromagnetic Waves
Conditions on the Wave Field
If the plane polarized waves is propagating along x-axis having electric vector along the y-axis, we have
CONDITIONS ON THE WAVE FIELD If the plane polarized waves is propagating along x-axis having electric vector along the y-axis, we have Ey ≠ 0, Ez = Ex = 0 and Similarly for magnetic field vector Hz ≠ 0, Hy = Hx = 0 Therefore, the wave equations for plane electromagnetic wave reduce to since at the given value of x, Ey and Hz are constant at any instant. Further Substituting eqn (7) in eqn (3) and eqn (8) in eqn (4) we have Solutions of the plane Wave Equations The plane wave equations for electric field and magnetic field are given by c- speed of EM wave The solutions of the above wave equations of progressive wave are given by where, ω - angular frequency k - wave vector Here E0 and H0 are the maximum values (amplitudes) of the electric and magnetic vectors respectively. The general solution of the wave equation is written as where c is the wave velocity. 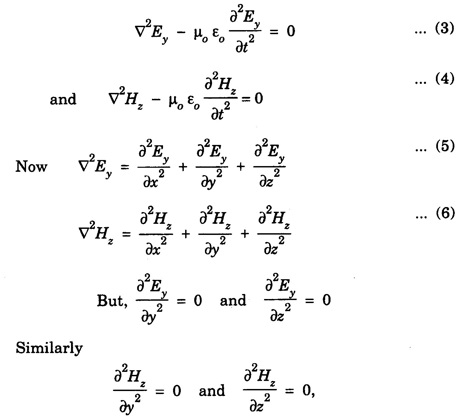
![]() and
and ![]() are varying only in x-direction which is the direction of propagation of these fields as shown in fig. 2.4.
are varying only in x-direction which is the direction of propagation of these fields as shown in fig. 2.4.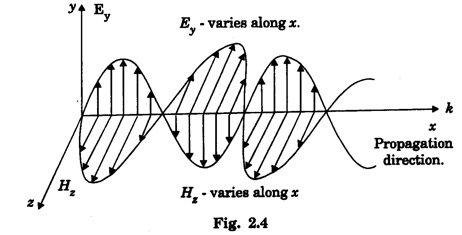
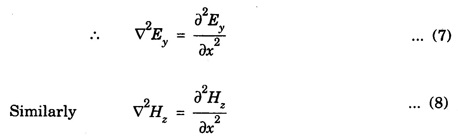
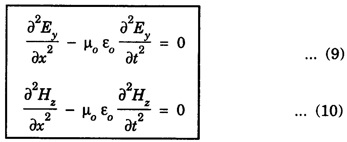
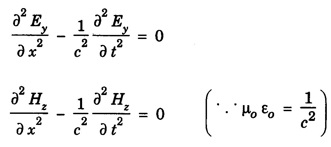

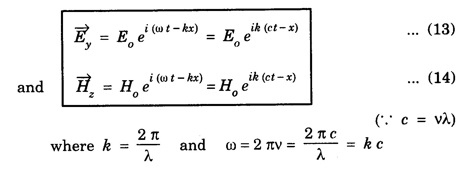

Engineering Physics: Unit II: Electromagnetic Waves : Tag: : - Conditions on the Wave Field
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
