Engineering Mechanics: Unit III: Distributed Forces
Centre of Gravity, Centre of Mass and Centroid
with Solved Example Problems
The gravitational force acts on each and every particle of the object.
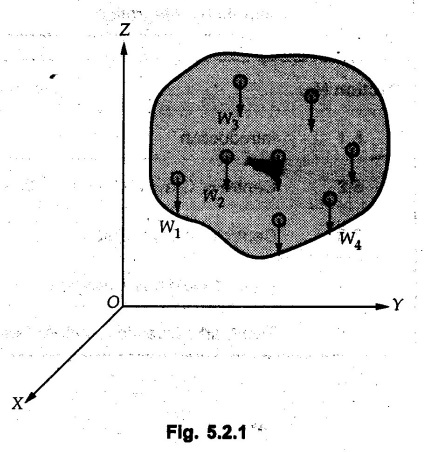
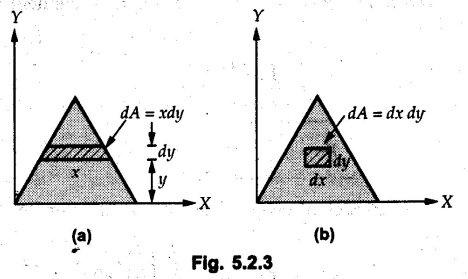
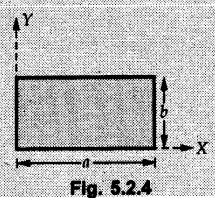
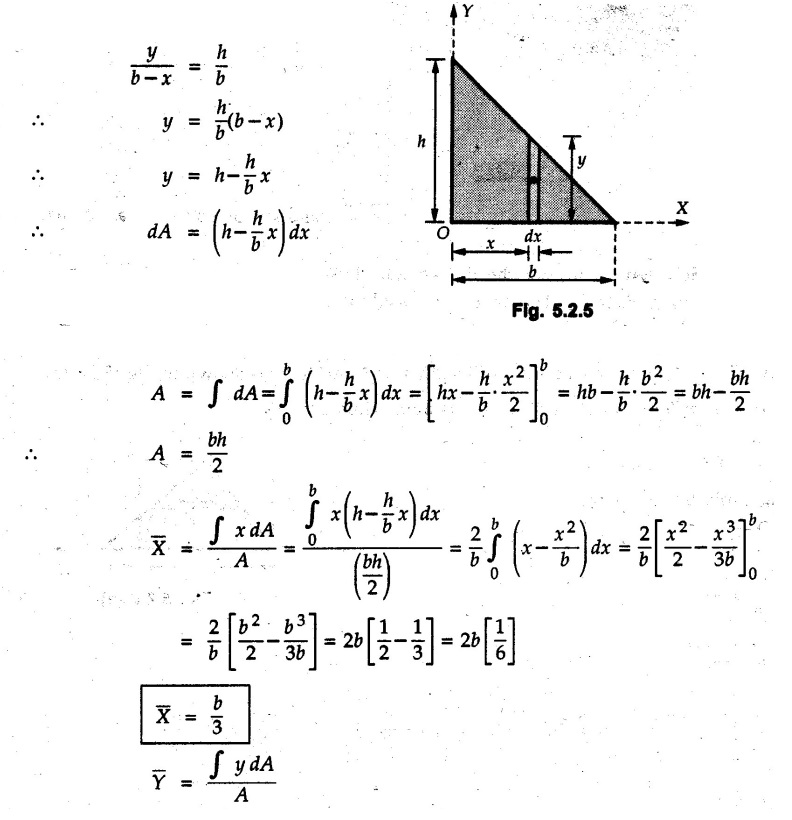
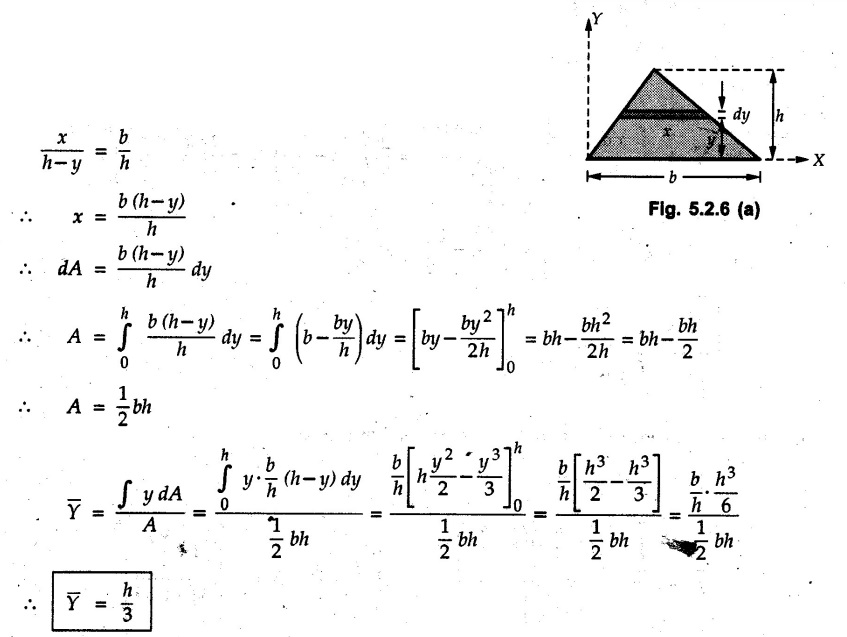
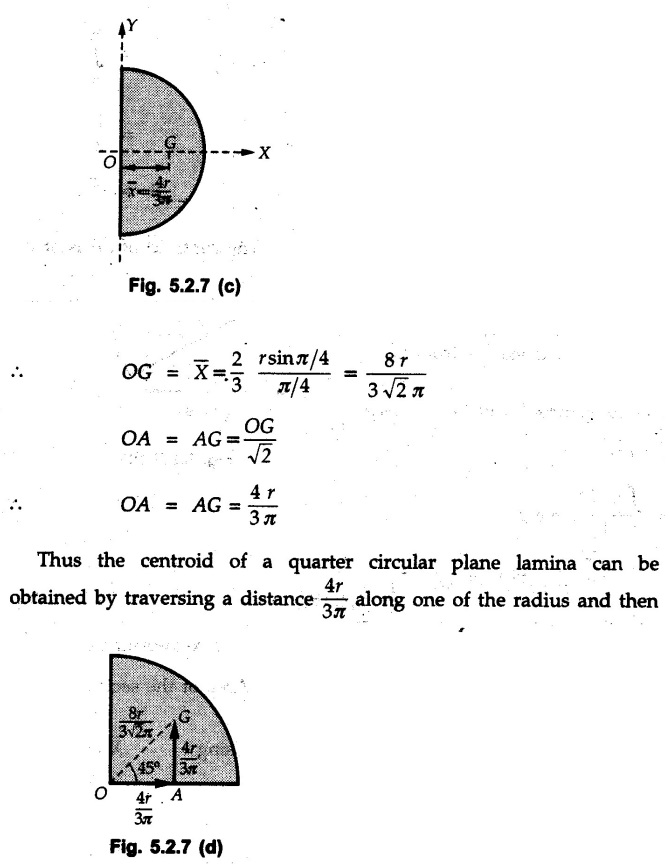
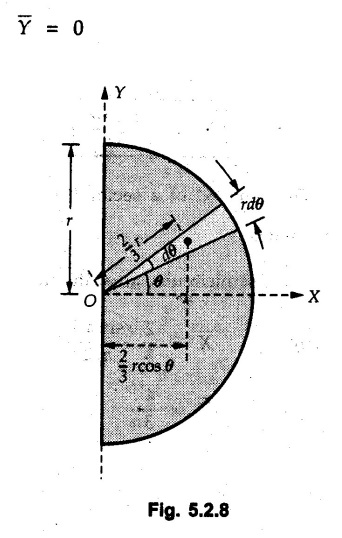
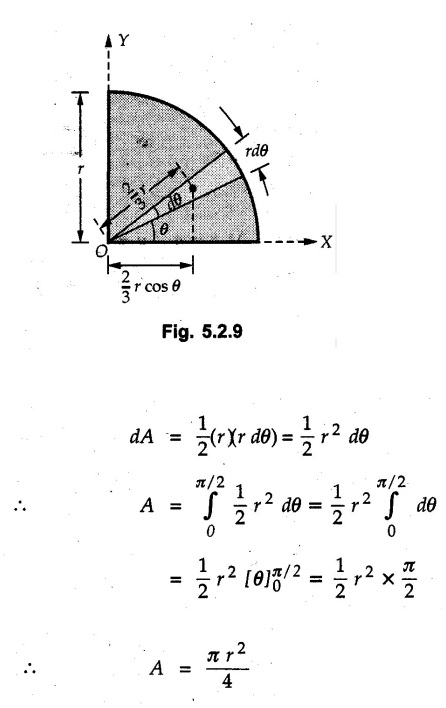
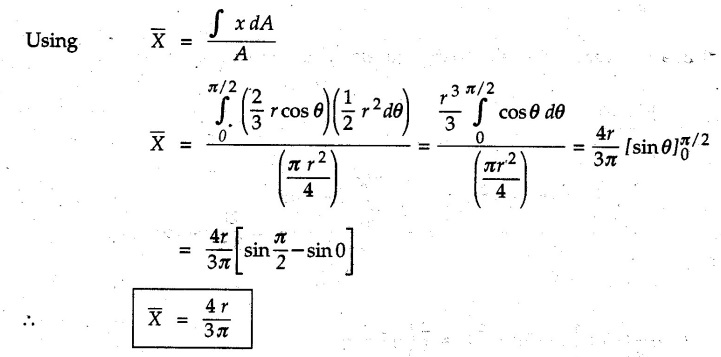
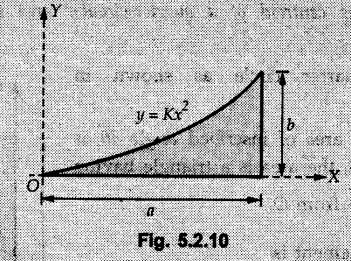
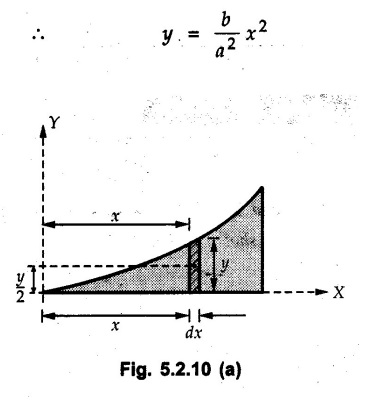
Centre of Gravity, Centre of Mass and Centroid • Let us consider an object as shown in Fig. 5.2.1. • The gravitational force acts on each and every particle of the object. • These forces act towards the centre of the earth and their magnitude depends on the distance from the centre of the earth. • However, for all practical purposes, we can consider all these forces to be parallel and to be of same magnitude for particles of same mass as the dimensions of the object would be very small compared to radius of earth. • These parallel forces can be reduced to a single force (weight of the object) acting through a point called the centre of gravity. • The magnitude, direction and point of application of the resultant force can be obtained using method described in chapter 3. • Consider an element of weight dW as shown in Fig. 5.2.2. • The total weight W can be obtained by adding weights of all the elements of the object. i.e., W ∫ dW • The point of application of W (ie., centre of gravity G) can be obtained using Varignon's theorem. • The moment of the element about Y-axis is x·dW. The sum of all these moments is ∫xdW. By Varignon's theorem, this must be equal to the moment of the resultant force W about the Y-axis which is W • The position of centre of gravity G is located by co-ordinates • Substituting W = mg, so that dW = g dm, the equations of position co-ordinates of centre of gravity become • The point defined by the above three equations is called centre of mass. It does not depend on the acceleration due to gravity. • In space, at a point, where there is no gravity, we cannot define centre of gravity but we can define centre of mass. • If density ρ of the object is constant throughout the object we can write its mass as m = ρ v Where v is the volume ⸫ dm = ρ dv The equations for position co-ordinates of centre of mass become • Note that these equations are independent of the mass distribution and hence represent the geometrical centre of the object. • The gemetrical centre of the object is known as centroid. • Thus, the above three equations represent position of centroid of volumes. • For slender rods or wires of uniform cross-section area A and constant density ρ, the volume can be written as V = A l ⸫ dv = A dl The equations (5.2.3 a, b, c) reduce to • The above equations represent centroids of lines. • For plane laminae, the density ρ and the thickness t are constant throughout. The volume of plane lamina can be written as V = At ⸫ dV = t dA • The equations (5.2.3 a, b, c) then reduce to • These equations represent position of centroid of plane laminae (area segments). Note: • The centroid always lies on the axis of symmetry. If there are two or more lines of symmetry, the centroid is the point of intersection of the lines of symmetry. • The centroid may lie outside the object. General procedure to find centroid by integration 1) Choose appropriate co-ordinate system depending upon symmetry of the problem. e.g. for circular arcs, the polar co-ordinate system will be more convenient to use than the rectangular cartesian co-ordinate system. 2) Choose a suitable differential element. For areas choose differential element of area dA. Choose first order differential element so that only one integration will be required to cover the complete area. Second order differential elements will require double integration. e.g., for a triangle, it will be more convenient to take a differential element shown in Fig. 5.2.3 (a) than the element shown in Fig. 5.2.3 (b). 3) Determine the co-ordinates of the centroid of the differential element. 4) Evaluate the integrals in equations (5.2.4 a, b) or (5.2.5 a, b) to find co-ordinates of centroid. Example 5.2.1 Determine the x and y co-ordinates of centroid of the rectangle shown in Fig. 5.2.4 from first principles. Solution : Consider the differential element to be a vertical strip of width dx as shown in Fig. 5.2.4 (a). The area of rectangle is A = a b The area of differential element is dA = b dx ⸫ A = ab The distance of centroid of differential element from Y-axis is x. The distance of centroid of differential element from X-axis is b/2. Example 5.2.2 Find the centroid of the area enclosed by a right angled triangle from first principles. Solution: Consider a right-angle triangle of base b and height h as shown in Fig. 5.2.5. Consider an elementary strip of width dx and height y parallel to Y-axis as shown.. As dx is very small, it is approximately a rectangular area. Its area is dA = y dx By similarity of triangles, where y is the centroidal distance of area dA from x-axis. Example 5.2.3 Determine the Y-co-ordinate of centroid of the triangular area of base b and height h shown in Fig. 5.2.6 from first principles. Solution : Consider a horizontal strip of length x and width dy as shown in Fig. 5.2.6 (a) The area of differential element which is approximately a rectangle, is dA = x dy Using similarity of triangles, Example 5.2.4 Obtain centroidal distance for a sector of angle 2a from first principles. Use it to locate centroid of semicircular and quarter circular plane laminae. Solution: Consider a sector as shown in Fig. 5.2.7 (a) with inscribed angle 2 α. Let the X-axis be the axis of symmetry. Then, Consider a triangular element as shown in Fig. 5.2.7 (b). The area of the triangular element will be The centroid of a sector lies on the line of symmetry at a distance of For a semicircular area, the inscribed angle is 2α = π, i.е., α = π/2 radians. Thus, for a semicircular area, the centroid is at a distance of 4r / 3π from the centre on the axis of symmetry as shown in Fig. 5.2.7 (c). For a quarter circular area the inscribed angle is 2α = π/2, i.e., α = π/4 radians Thus the centroid of a quarter circular plane lamina can be obtained by traversing a distance 4r / 3π along one of the radius and then again a distance 4r / 3π in a perpendicular direction as shown in Fig. 5.2.7 (d). Example 5.2.5 Determine the centroid of a semi-circular area of radius r from rst principles. Solution : Consider a semicircle as shown in Fig. 5.2.8. As the x-axis is the axis of symmetry. Consider an elementary area of inscribed angle dθ as shown in Fig. 5.2.8. As dθ is very small, the area is a triangle having its centroid at distance 2r /3 from O. The area of the triangular element is The x- co-ordinate of centroid of the triangular elementary area is 2/3 r cos θ. The centroid of a semicircle lies on the line of symmetry at a distance of 4r/3π from the centre. Example 5.2.6 Determine the centroid of a quarter-circular area of radius r from first principles. Solution: Consider a quarter circle as shown in Fig. 5.2.9. Consider an elementary area of inscribed angle de as shown. As de is very small, the area is a triangle having its centroid at a distance 2r/3 from O. The area of triangular element is The x- co-ordinate of centroid of the triangular elementary area is 2r/3 cos θ. The line of symmetry is a line making angle 45° with X-axis. This line divides the quarter circle into two equal areas. As centroid lies on this line of symmetry, Example 5.2.7 Determine co-ordinates of centroid of the shaded region shown in Fig. 5.2.10. Solution: At x = a, y = b ⸫ y = Kx2 ⇒ b = Ka2 ⸫ K = b/ a2 Consider the differential element to be a vertical strip of width dx and height y as shown in Fig. 5.2.10 (a). Area of differential element is dA = y dx The distance of centroid of differential element from Y-axis is x. The distance of centroid of differential element from X-axis is y/2.Centre of gravity
![]()
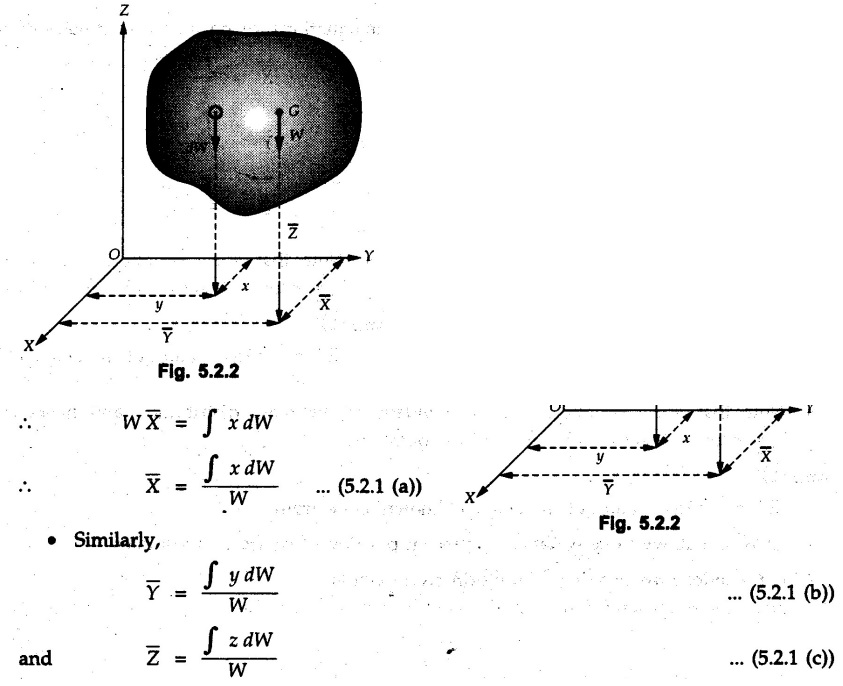
 which are obtained using equations (5.2.1 (a)), (5.2.1 (b)) and (5.2.1 (c))
which are obtained using equations (5.2.1 (a)), (5.2.1 (b)) and (5.2.1 (c))Centre of mass


Centroid


Solved Examples for Understanding
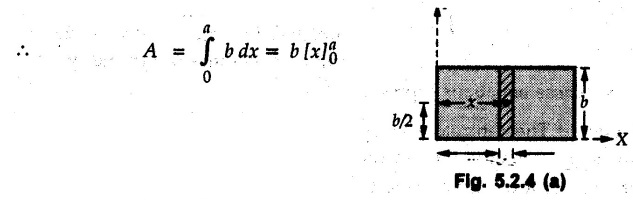
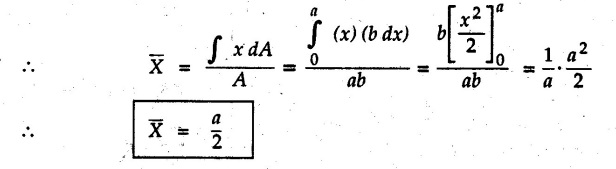
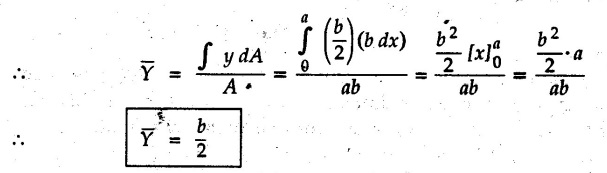
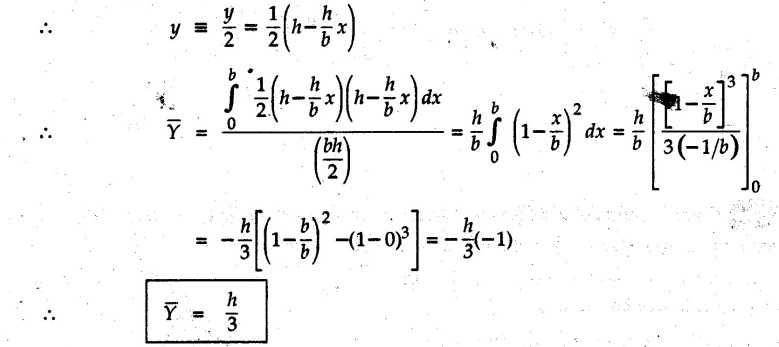
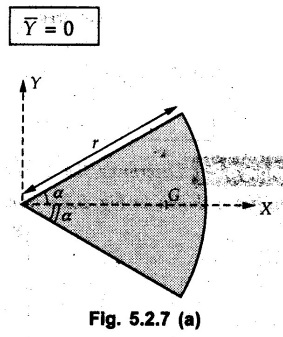
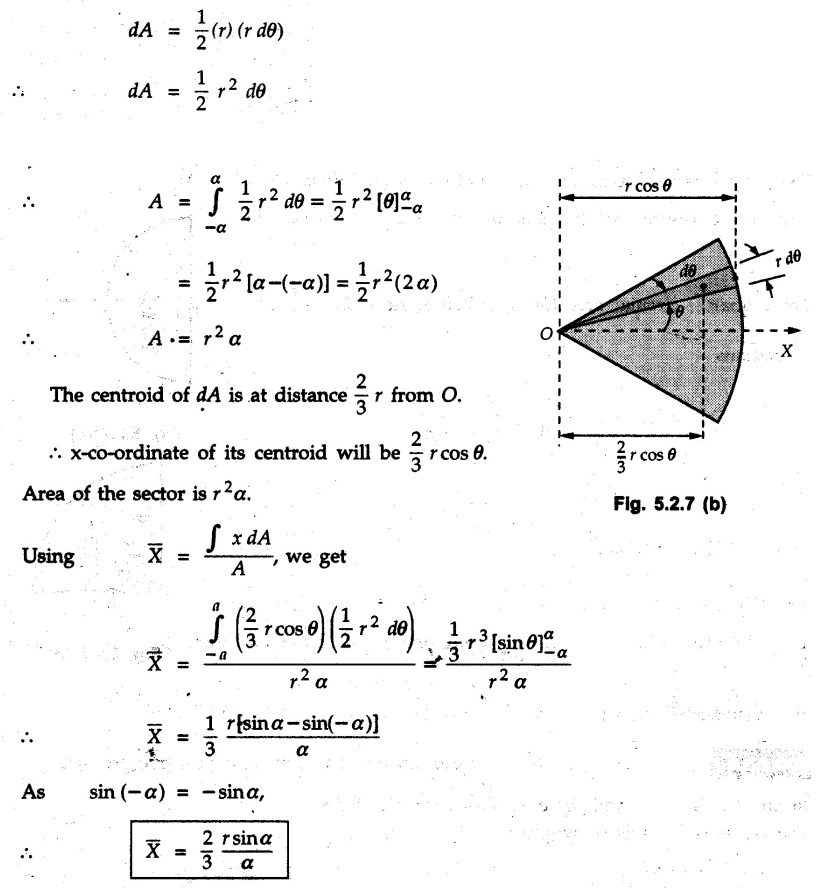
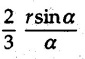 from the centre.
from the centre.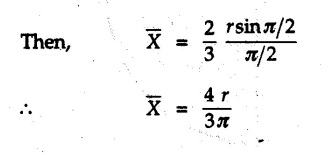
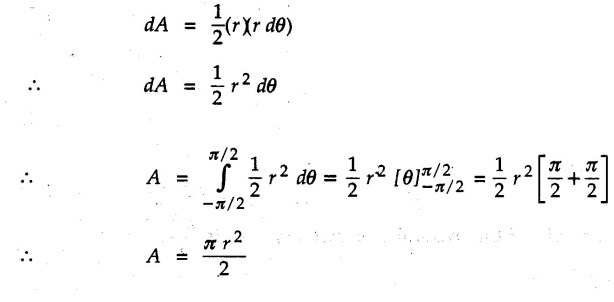
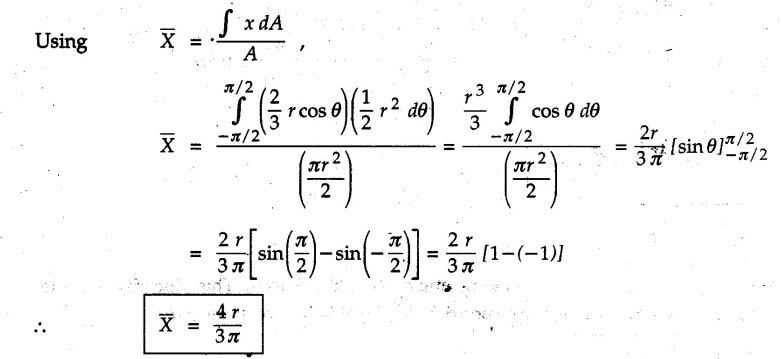
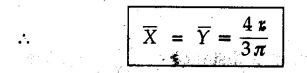
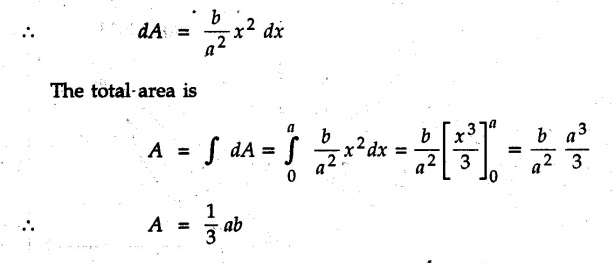
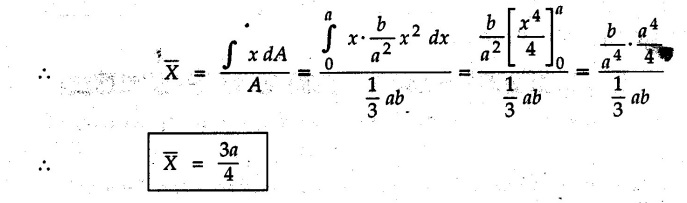
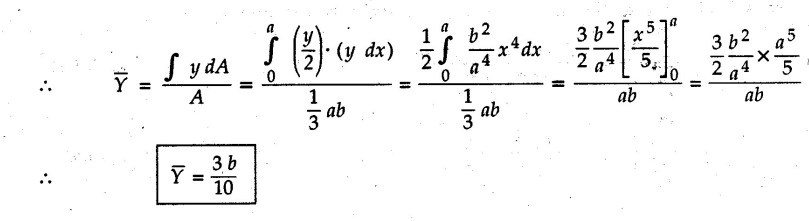
Engineering Mechanics: Unit III: Distributed Forces : Tag: : with Solved Example Problems - Centre of Gravity, Centre of Mass and Centroid
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
