Engineering Mechanics: Unit IV: Friction
Belt Friction (Flat Belts)
with Solved Example Problems
Consider a flat belt passing over a pulley or any cylindrical surface as shown in Fig. 8.9.1.
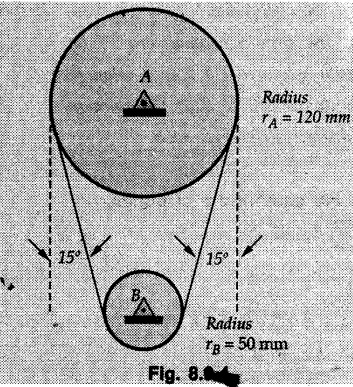
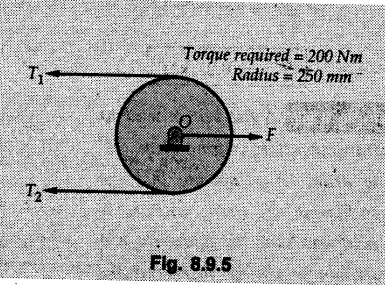
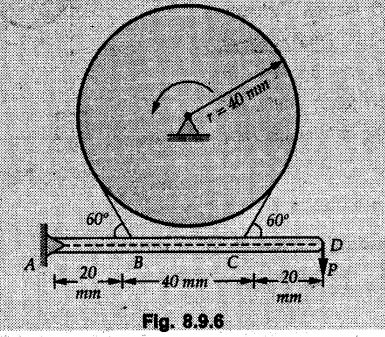
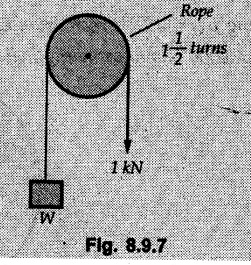
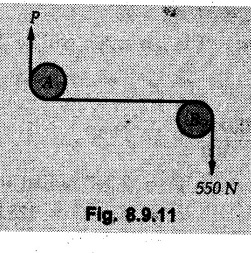
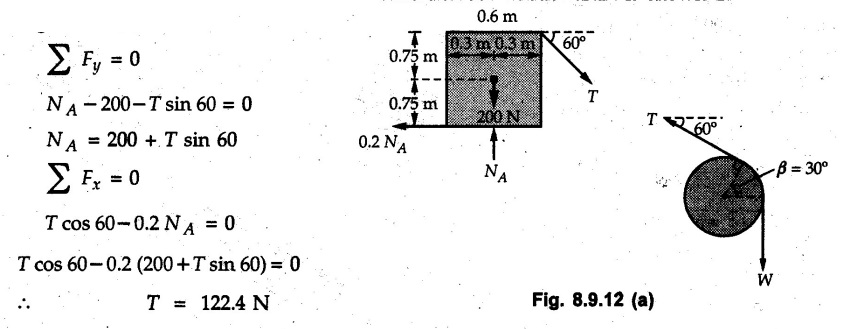
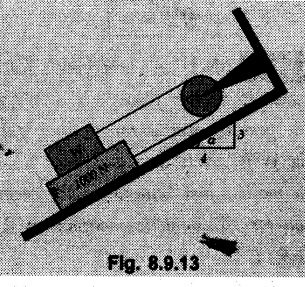
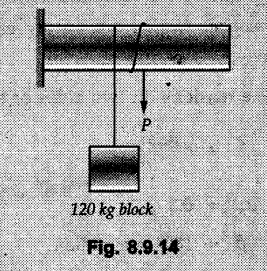
(Flat Belts) • Consider a flat belt passing over a pulley or any cylindrical surface as shown in Fig. 8.9.1. • If there is no friction between pulley and the belt, the tensions T1 and T2 will be equal in magnitude. • In presence of friction, the two tensions will have different magnitudes. • We will now develop a formula relating T1 and T2, assuming T2 > T1. • The belt leaves the pulley tangentially at A and D as shown in Fig. 8.9.1. • The inscribed angle over which belt is in contact with the pulley is called the lap angle β. ⸫ β = ∠AOD • Consider F.B.D. of a differential element BC of inscribed angle dθ as shown in Fig. 8.9.2. • Substituting in equation (8.9.1), • Integrating, we get • In the above equation, value of β has to be in radians. μ can be either μk or μs depending upon whether there is relative motion between belt and pulley or not. • If number of turns of the rope or belt are given, around the pulley, the value of β in radians can be obtained using 1 Turn = 2л radians. • If number of turns are not given, use the concept that rope or belt leaves the pulley tangentially. Draw radii at the points where the belt leaves the pulley and find the inscribed angle for which the belt is in contact with the pulley. • As tensions on two sides of the pulley are different, a net torque acts on the pulley given by where r = Radius of the pulley • If belt drives the pulley, the driving torque and rotation of pulley will have same sense of rotation. • For braking mechanisms, the torque will be opposite to the rotation of pulley. • This is useful in identifying larger tension (T2) and smaller tension (T1). Steps for Solution : 1) Find lap angle β in radians. 2) Identify the larger tension (T2) and smaller tension (T1). 3) Use T2/ T1 = eμβ for the pulley. 4) If required, use additional equations 5) Solve the equations simultaneously. Example 8.9.1 A rope is wrapped three times around a rod as shown in Fig. 8.9.3. Determine the force T required on the free end of the rope, to support a load of W = 20 kN. Take μ as 0.30. Solution: Example 8.9.2 A flat belt is used to transmit a torque from drum 'B' to drum 'A'. Knowing that the coefficient of static friction is 0.40 and that the allowable belt tension is 450 N, determine the largest torque that can be exerted on drum 'A'. Refer Fig. 8.9.4. Solution: Note that the sense of rotation for the drums is not given and hence we can take tension on any one side to be the larger tension. Example 8.9.3 A drum requires a torque of 200 N-m to get it to start rotating. If the static coefficient of friction μs between the belt and drum is 0.35, what is the minimum axial force. F on the drum required to create enough tension in the belt to start the rotation of the drum ? Refer Fig. 8.9.5. Solution: For equilibrium of pulley, Example 8.9.4 As shown in Fig. 8.9.6 a flexible and inextensible flat belt placed around a rotating drum of 40 mm radius, acts as a brake when the arm ABCD is pulled down. Assuming = 0.2 between drum and belt, find the force 'P' that would result in braking torque of 4000 N.mm assuming that the drum is rotating counter clockwise. Solution: The two free body diagrams are shown in Fig. 8.9.6 (a). As the drum is rotating counter clockwise, the braking torque will be clockwise. Hence TC > TB for the drum, Example 8.9.5 A rope makes 1 turns over a fixed cylinder as shown in Fig. 8.9.7. Angle of friction between rope and cylinder is 10°. Find range of values of 'W' that can be kept in equilibrium by 1 kN force. State the condition of impending motion in each case. Solution: For minimum value of W, W< 1 kN and impending motion of 'W' is upwards. Example 8.9.6 A band brake has flat leather belt on a 0.6 m diameter drum. For u≈ 0.25 between belt and drum and clockwise rotation of drum, calculate braking torque. Refer Fig. 8.9.8. Solution: For clockwise rotation of the drum, the braking torque is anticlockwise. TB > TA Example 8.97 A flexible cable which supports the 100 kg load, is passed over a fixed circular drum and subjected to a force P = 500 N to maintain equilibrium. If coefficient of static friction between cable and the fixed drum is 0.3, determine the minimum value which the angle 'α' may have before the load begins to slip. Refer Fig. 8.9.9. Solution: The lap angle will be β = 90° + α Example 8.9.8 A rope is wrapped around a horizontal bar for 2 1/2 turns, as shown in Fig. 8.9.10. By exerting a force of 800 N at the free end of the rope, one can just support a load of 60 kN on the other end. Determine i) The coefficient of friction and ii) The number of times the rope should be wrapped around the bar to support a load of 200 kN with the same force of 800 N applied at the free end. Solution: i) The larger tension is T2 = 60 kN = 60 × 103 N and smaller tension T1 = 800 N. Example 8.9.9 A load of 550 N is just prevented from falling, by a rope wrapped ¼ turn around a fixed drum B and 17 turn around another fixed drum A. Assuming the drum B to be smooth and the co-efficient of friction between the rope and drum A to be 0.25, what is the value of the holding force P? Refer Fig. 8.9.11. Solution: As drum B is smooth, tension on both sides of B will be same, i.e., 550 N. For holding force P, i.e., the minimum force required to prevent the downward motion of the 550 N load, Example 8.9.10 Block A weighing 200 N is connected to another block B of weight W, by a cord passing over a rough fixed pulley. The weight W is slowly increased. Find its value for which motion just impends. Take coefficient of friction for all contacting surfaces = 0.2. Refer Fig. 8.9.12. Solution: The block A can either slide or overturn. The value of 'T to cause sliding can be obtained using limiting equilibrium condition for which F.B.D. is shown in Fig. 8.9.12 (a). The value of 'T’ to cause overturning is obtained by shifting 'NA' to the right edge and using moment equation about the right edge. (200) (0.3) – (T cos 60 ) (1.5) = 0 T = 80 N As 'W' increases, T also increases. As the value of T is smaller for overturning, the impending motion is overturning for block A and corresponding value of T is 80 N. Using F.B.D. of pulley, Example 8.9.11 Determine the minimum weight W to prevent downward motion of the 1000 N body. Take μ = 0.2 between the rope and the fixed drum and μ = 0.3 for other surfaces of contact. Refer Fig. 8.9.13. Solution: For minimum weight 'W', the impending motion of 1000 N. is down the incline and for 'W' it is up the incline. The free body diagrams are shown in Fig. 8.9.13 (a). Example 8.9.12 A 120 kg block is supported by a rope which is wrapped one and half times around a horizontal rod. The coefficient of static friction between the rod and the rope is u,= 0.15, determine the range of values of P for which equilibrium is maintained. Refer Fig. 8.9.14. Solution: The relation between tension in the rope on two sides of the rod is Example 8.9.13 A cord having weight of 0.5 N/m and a total length of 10 m is supported over a peg P as shown in Fig. 8.9.15. If the coefficient of static friction between the peg and cord is μs= 0.5, determine longest length h which one side of the suspended cord can have without causing motion. Neglect size of peg and length of cord draped over it. Solution: The tensions on two sides of the peg are related as Example 8.9.14 A flat belt develops a tight side tension of 2000 N during power transmission, the coefficient of friction between pulley and belt is 0.3; the angle of lap on smaller pulley is 165° and the belt speed is 18 m/s. Determine the power that can be transmitted, if the belt is assumed to be perfectly elastic and without mass. Solution :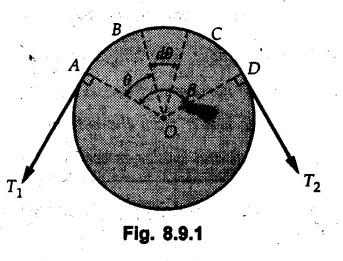
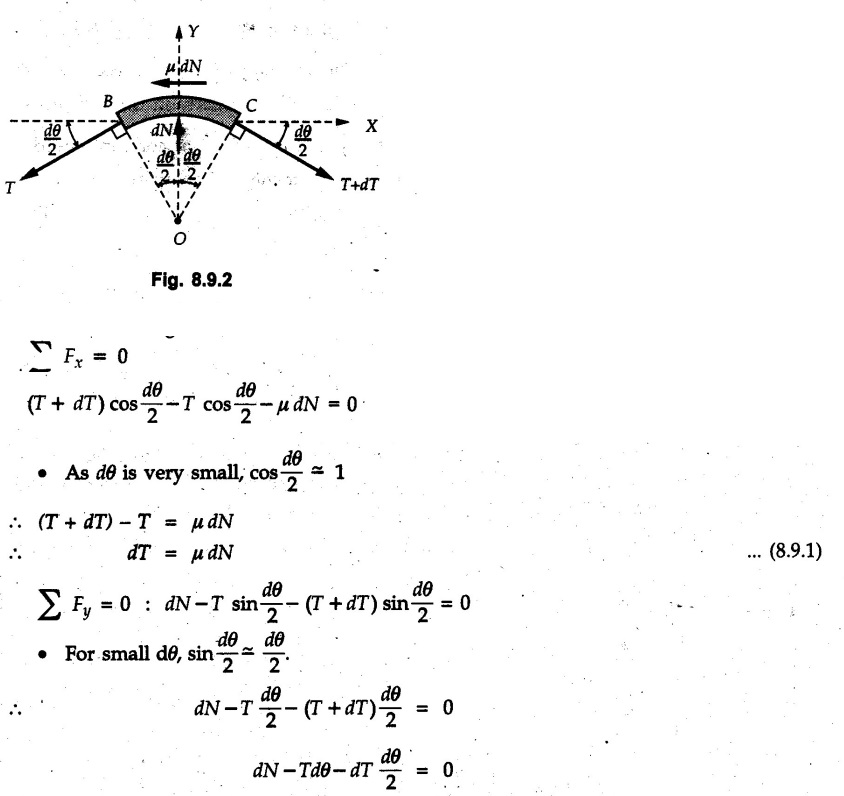 • dT · dθ /2 is a product of two differential quantities and hence is very small compared to the remaining terms.
• dT · dθ /2 is a product of two differential quantities and hence is very small compared to the remaining terms.
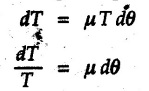


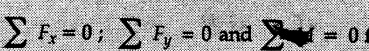 for the equilibrium of pulley or any other object like a lever connected to the pulley.
for the equilibrium of pulley or any other object like a lever connected to the pulley.Solved Examples for Understanding













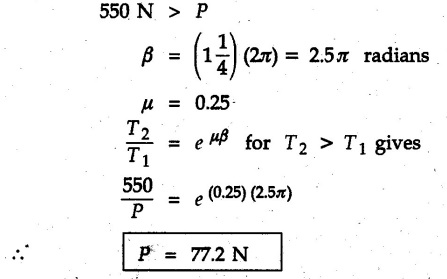

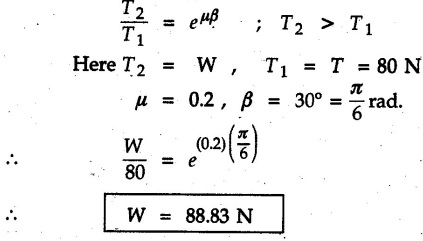



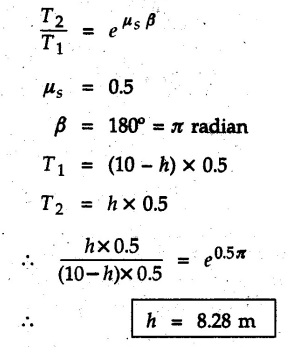

Engineering Mechanics: Unit IV: Friction : Tag: : with Solved Example Problems - Belt Friction (Flat Belts)
Related Topics
Related Subjects
Engineering Mechanics
ME3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
