Transforms and Partial Differential Equations: Unit V: Z - Transforms and Difference Equations
z - transforms
Applications, Elementary properties, Definition, Solved Example Problems
The Z-transform plays the same role for discrete systems as the Laplace transform does for continuous systems.
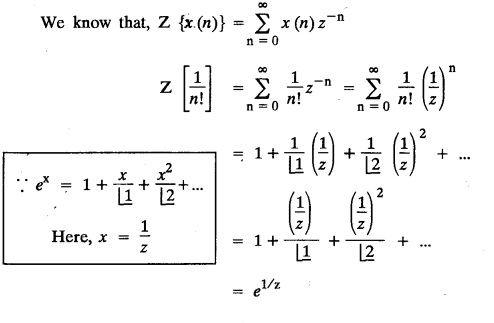
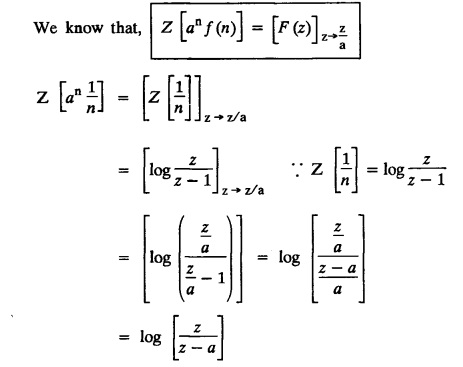
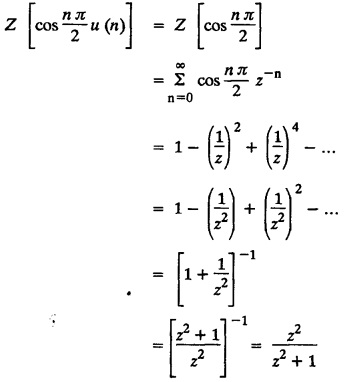
UNIT - V Z - TRANSFORMS AND DIFFERENCE EQUATIONS Z-transforms - Elementary properties - Inverse Z - transform (using partial fraction and residues) - Convolution theorem - Formation of difference equations - Solution of difference equations using Z-transform. The Z-transform plays the same role for discrete systems as the Laplace transform does for continuous systems. Applications of Z transform 1. Communication is one of the fields whose development is based on discrete analysis. Difference equations are also based on discrete system and their solutions and analysis are carried out by Z - transform. 2. In the system analysis area, the Z - transform converts convolutions to a product and difference equations to algebraic equations. 3. The stability of a discrete linear system can be determined by analyzing the transfer function H (z) given by the Z - transform. 4. Digital filters can be analyzed and designed using the Z - transform. 5. Digital control systems can be analyzed and designed using Z- transforms. 1. Z - transform, elementary properties of Z - transform Z - transform Definition: Z - transform (two-sided or bilateral) Let {x (n)} be a sequence defined for all integers then its Z-transform is defined to be where z is an arbitrary complex number. Definition: Z - transform (one-sided or unilateral) Let {x (n)} be a sequence defined for n = 0, 1, 2, ... and x (n) 0 for n < 0, then its Z- transform is defined to be where z is an arbitrary complex number. Definition: Z - transform for discrete values of t If f (t) is a function defined for discrete values of t where t = nT, n = 0, 1, 2, 3, ... T being the sampling period, then Z - transform of f(t) is defined as Note: 1. Mostly we study one-sided Z transform 2. If ƒ (t) given, then replace 't’ by ‘n T' 3. The double braces {} are used for a sequence. Sometimes we use [ ] or ( ). 1. Problems based on Z-transform of some basic functions Find the Z-transform of the following functions : 1. Prove that, Z [1] = Solution: 2. Prove that, Z [an] = Solution: 3. Prove that, Z (n) = Solution: 4. Prove that, Solution : 5. Prove that, Solution : 6. Prove that, Solution: 7. Prove that, Solution : 8. Find Solution: 9. Find the Z-transform of (n + 2) Solution: 10. Find Solution: 2. Linearity property : The Z - transform is linear Proof: Find the Z-transform of the following functions : 1. Find Z (K) Solution: 2. Find Z [(-1)n] Solution: 3. Find Z [(-3)n] Solution: 4. Find Solution : 5. Find Z [ean]. Solution : 6. Find Z [e-an] Solution: 7. Find Z [cos nθ] and Z [ sin nθ] Solution : Equating the real and imaginary parts, we get 8. Find Z [rncos nθ] and Z [rn sin nθ] Solution: Equating the real and imaginary parts, we get 9. Find Z (t). Solution: 10. Find Z [e-at] Solution: 11. Find Z [cos an] Solution: 12. Find Z [an-1] Solution : 13. Find Z [cosh α n] Solution : 14. Find Z [sinh 3n] Solution : III. Find the Z transform of the following: 1. Find Solution : 2. Find Solution : 3. Find Solution : 4. Find Solution : 5. (a) Find Solution : 5. (b) Find Solution : 6. Find Solution : 7. Find Solution : 8. Find Z [4.3n + 2 (−1)n] Solution: 9. Find Solution : 10. Find the Z-transform of Solution : Proof : Given: F(z) = Z [f(n)] IV. Find the Z-transform of the following: [Differentiation in the Z-Domain] 1. Find Z (n2) Solution: 2. Find Z (n3) Solution: 3. Find Z (nk) Solution : Which is a recurrence formula. 4. Find Z [an2 + bn + c] Solution : Z [an2 + bn + c] = a Z [n2] + b Z [n] + c Z [1] 5. Find Z [n (n - 1)] Solution: 6. Find Z [nC2] Solution : 7. Find Z [n cos nθ ] Solution: 8. Find Z [n (n − 1) (n − 2)] Solution : 9. Given that F (z) = log (1 + az -1), for |z| > |a |, find f(n) and also find Z[n_f(n)]. Solution : Given : F(z) = log (1 + az-1) 10. Find the Z-transform of {nCk}. Solution : This is the expansion of binomial theorem. = (1+z-1)n 11. Find the Z-transform of {k+nCn} Solution: 12. Find the Z-transform of (n + 1) (n + 2). Solution : Damping rule [The geometric factor a-n when a < 1, damps the function un. Hence we use the name damping rule] Proof: (i) Given: F(z) = Z {f(n)} V. Problems based on first shifting theorem [Frequency shifting] Find the Z-transform of the following: 1. Find Z [an n] Solution : 2. Find Solution : 3. Find Solution: 4. Find Z [an sin n θ] Solution: 5. Find Z [an cos n θ] Solution: 6. Find Z [an rn cos nθ] Solution : Aliter : 7. Find Z [(n – 1)an-1] Solution : 8. Find Z [an cos nπ] Solution: 9. Find Z [an n3] Solution: 10. Find Z [a-nn2] Solution: 11. Find Z [2n n2] Solution: 12. Find Z [2n sinh 3n] Solution: 13. Find Z [an cosh α n] Solution : 14. (i) Find Solution: VI. Problems based on Time shifting Find the Z-transform of the following: 1. Find Solution : 2. Find Z [cos (n + 1) θ] Solution : 3. Find Z [sin (n − 1)θ] Solution : Definition: Unit impulse sequence The unit impulse sequence d (n) is defined as the sequence with values (1) Z-Transfrom of unit impulse sequence is 1. i.e., Z [δ (n)] = 1 Proof : Definition: Unit step sequence The unit step sequence u (n) has values (2) Z-transform of unit step sequence i.e., Z (u (n)}= Proof : (3) Z-transform of Proof : VII. Find the L-transform of the following. (based on unit impulse sequence and unit step sequence) 1. Find Z [δ (n − k)] Solution: 2. Find Z [an δ (n − k)] Solution: 3. Find Z [2n δ (n − 2)] Solution: 4. Find Z [3n δ (n − 1)] Solution: 5. Find Z [u (n - 1)] Solution: 6. Find Solution : 7. Find Solution : 1. Initial value theorem Proof : 2. Final value theorem. Proof : 1. If F (z) Solution : By Initial value theorem By Final value theorem we get 2. If Solution: By Initial value theorem : 3. If Solution: By Initial value theorem : 1. If Solution : IX. Problems based on Find the Z-transform of (i) n an u (n) ; (ii) n (n − 1) an u (n) Solution: Note: Put a = 1, we getIntroduction
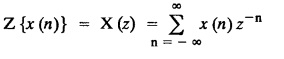
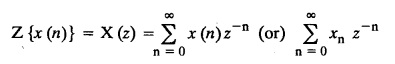
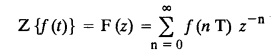
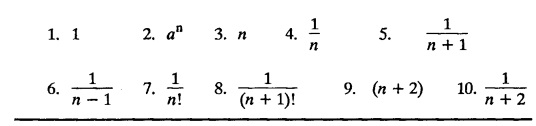
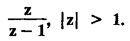
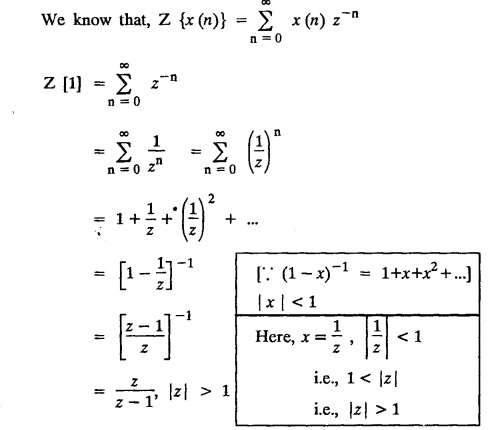
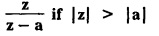

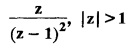

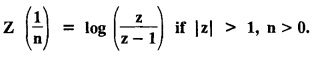

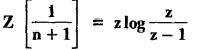

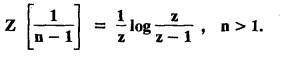
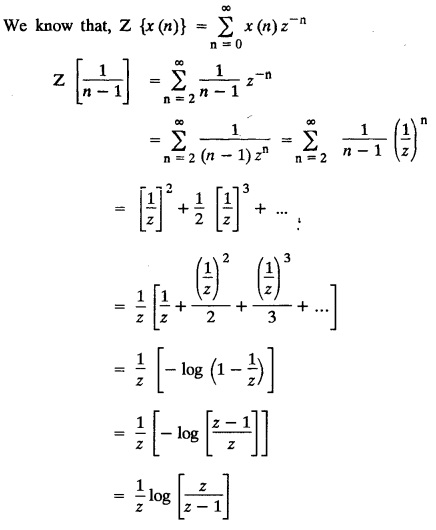
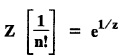
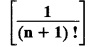

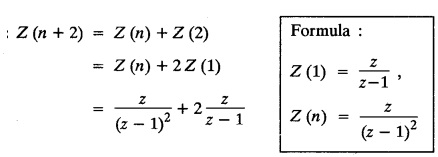
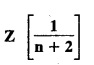

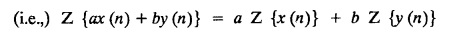
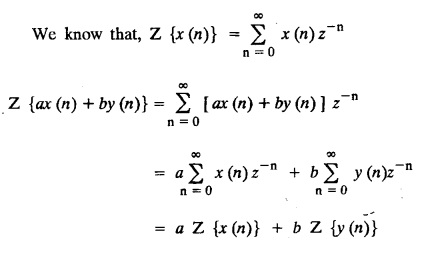
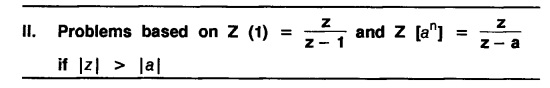
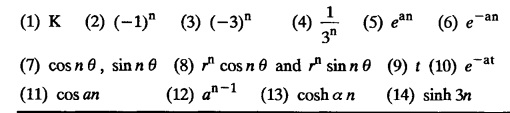
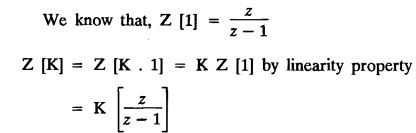
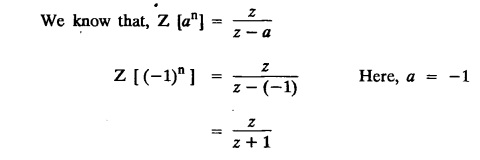
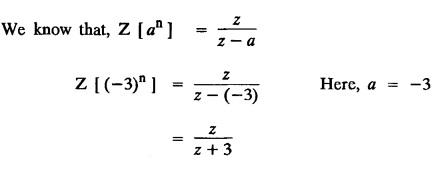
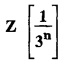
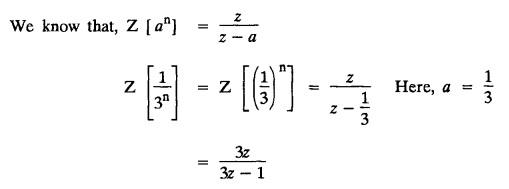
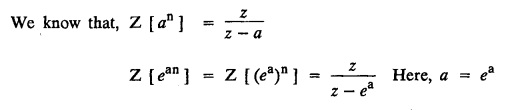
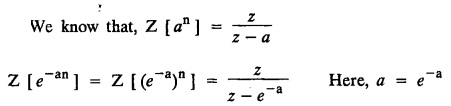
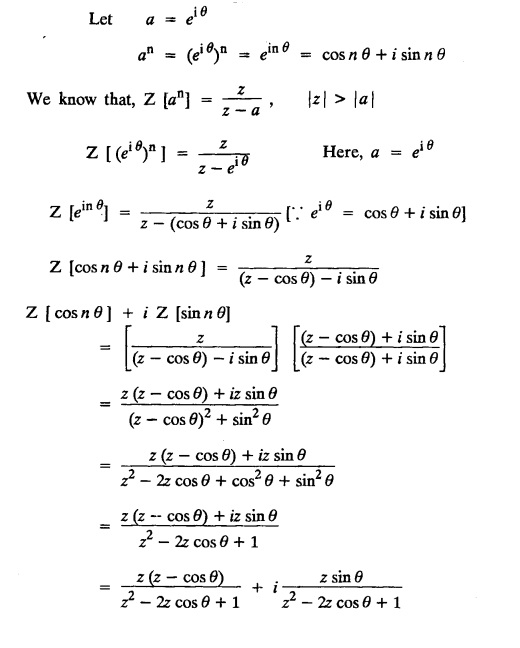
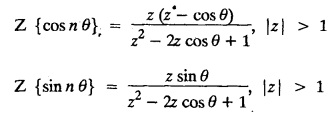
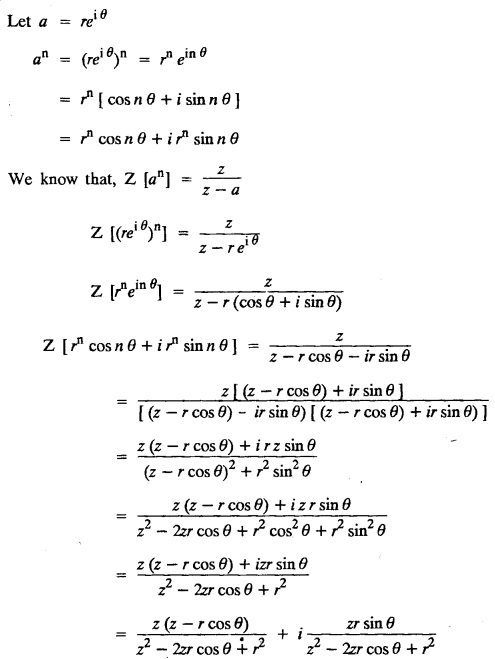
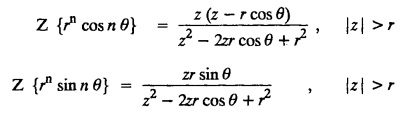
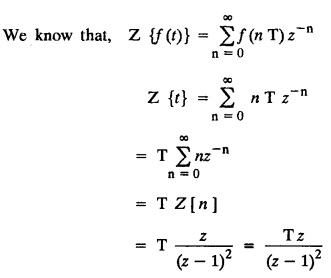
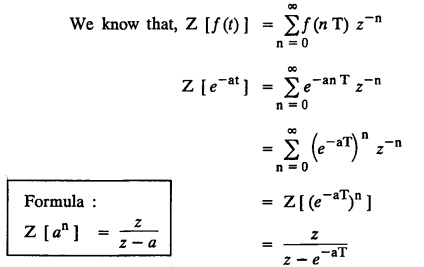
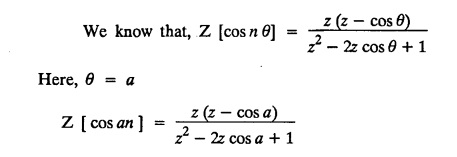
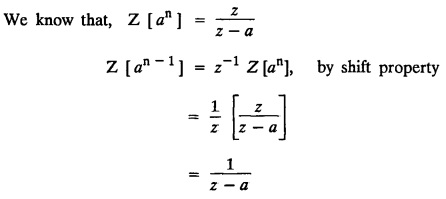
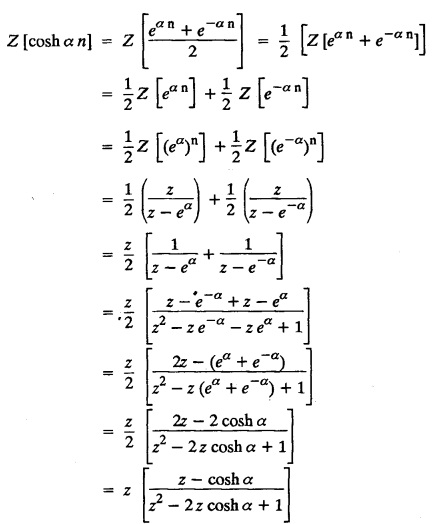

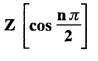
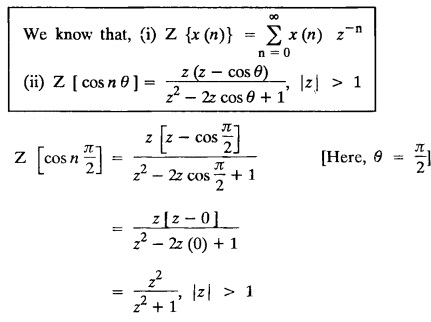
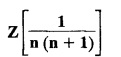

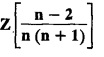

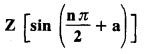

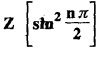

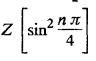
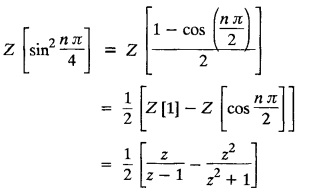
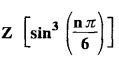

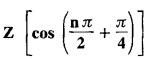

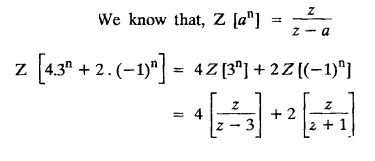
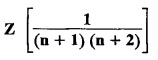
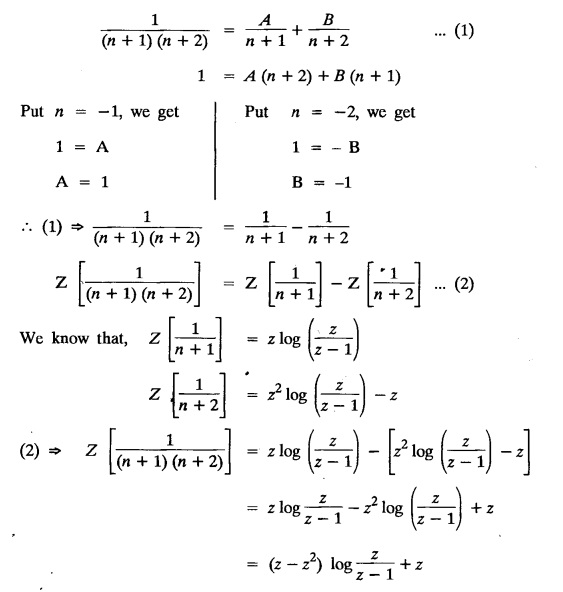
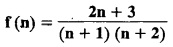
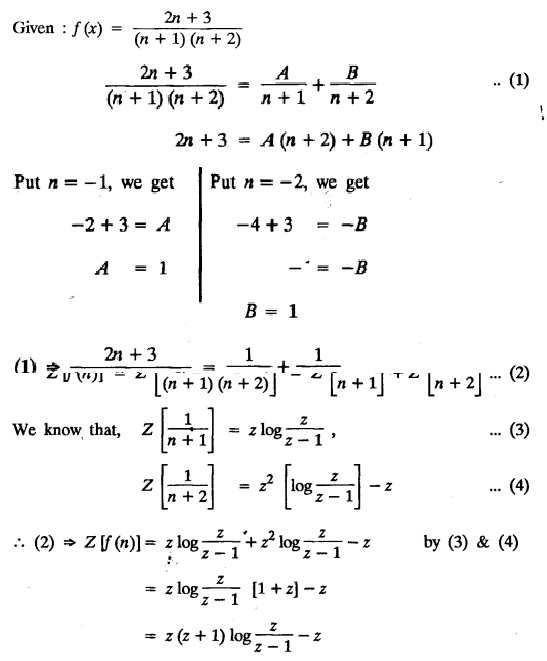 3. Differentiation in the Z-Domain
3. Differentiation in the Z-Domain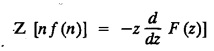
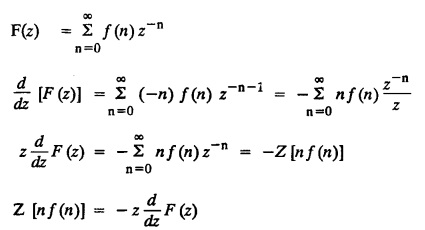
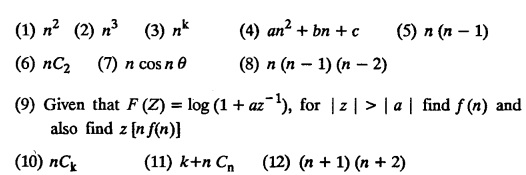
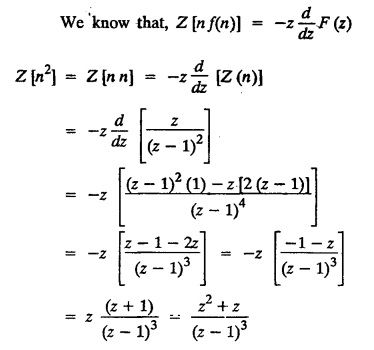
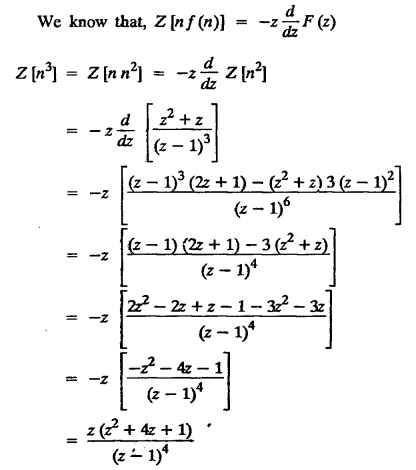
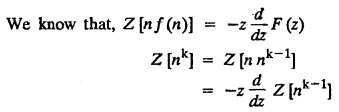
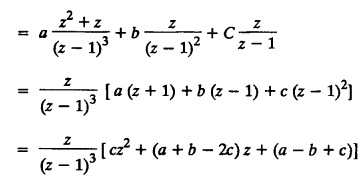
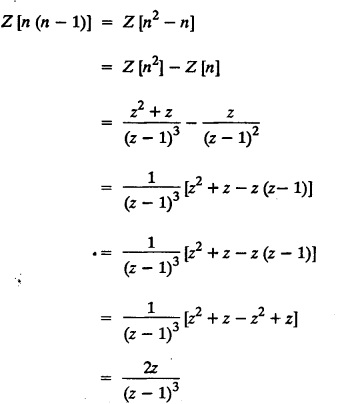

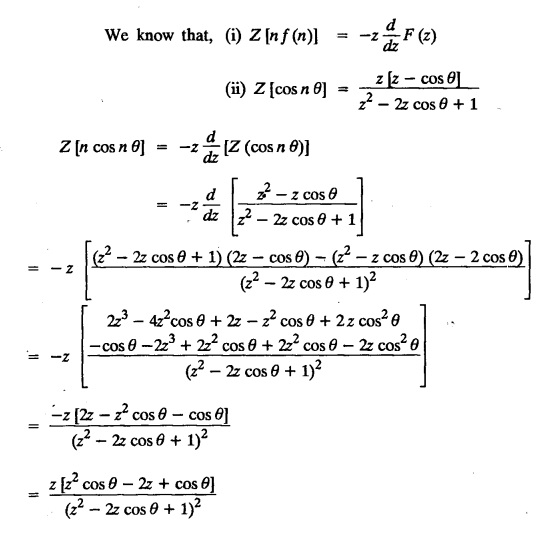


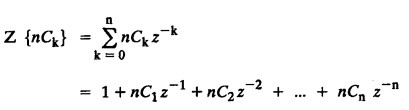
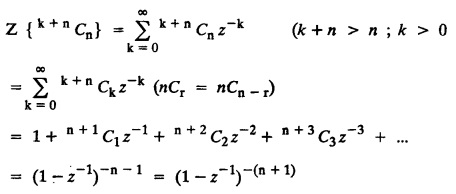
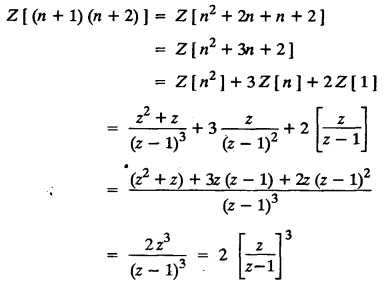
4. First Shifting theorem [Frequency shifting]:
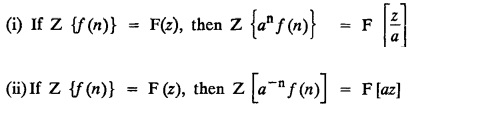

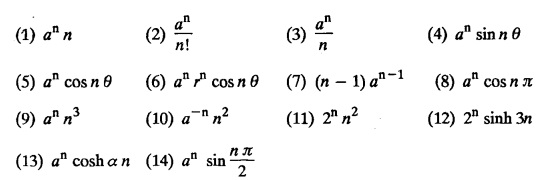

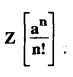
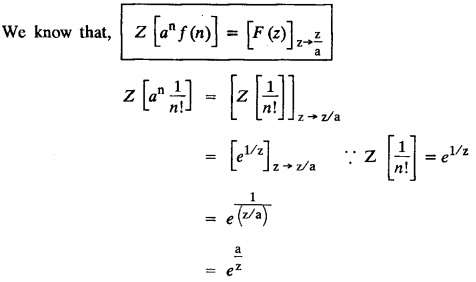
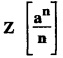
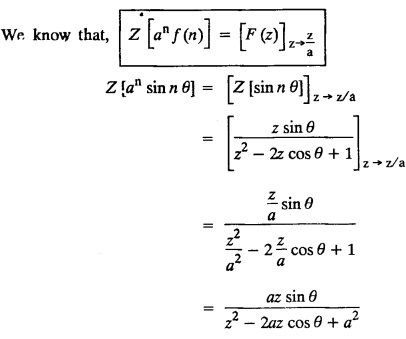
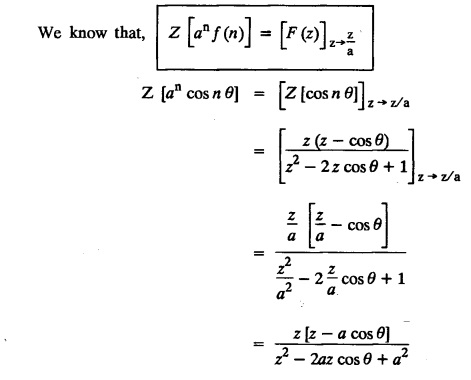
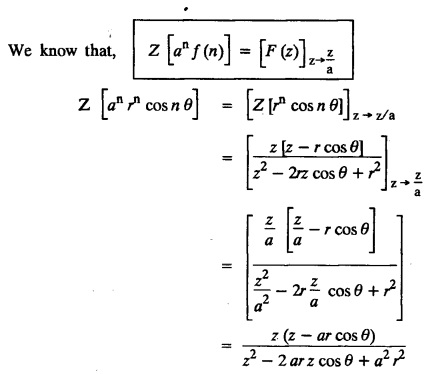
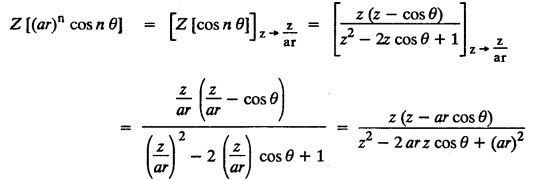
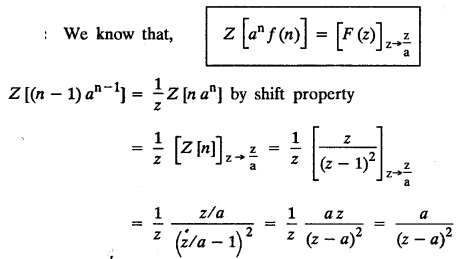

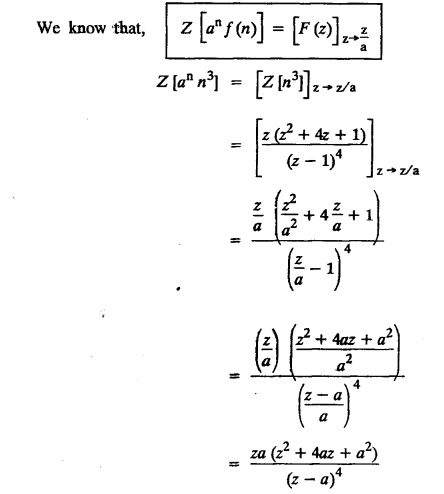
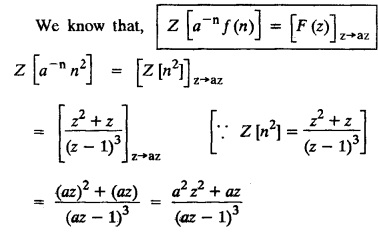



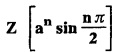

5. Second shifting theorem [Time Shifting]

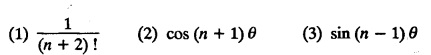
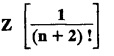
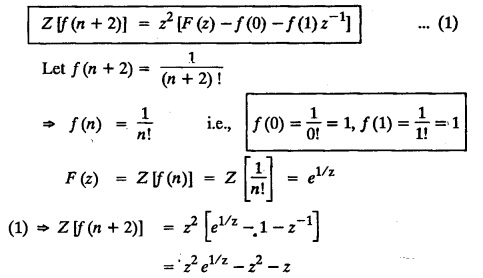

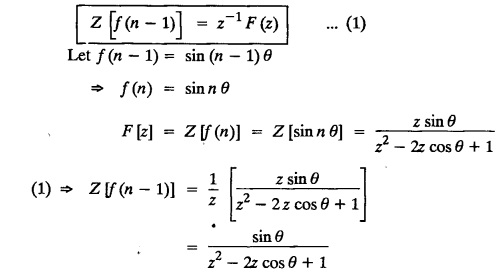
6. Unit impulse sequence and unit step sequence.
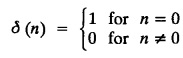
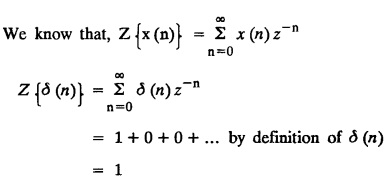
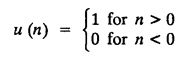
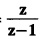

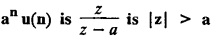
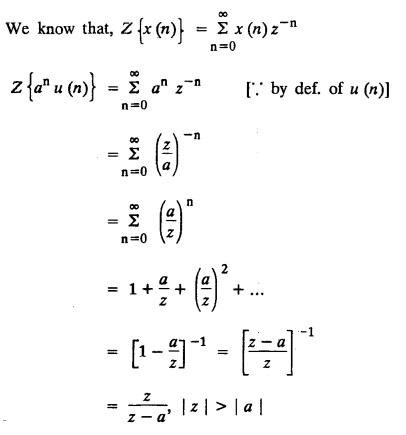
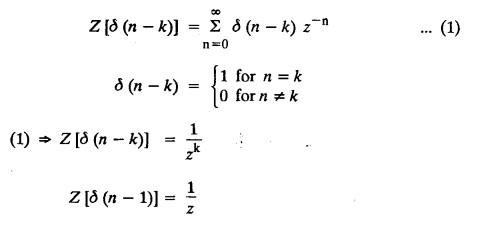
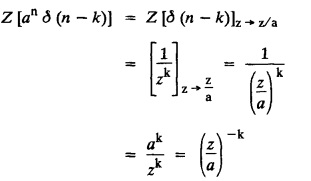
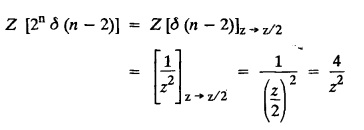
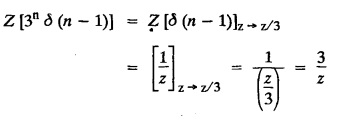
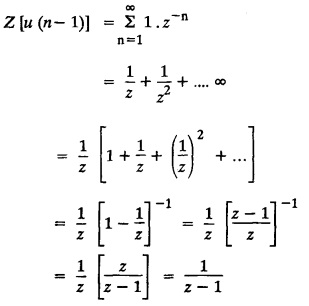
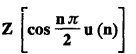
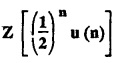
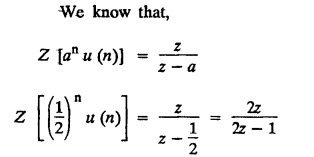
7. Initial value theorem and final value theorem.
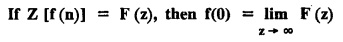
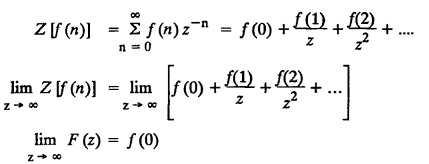
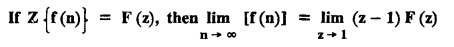
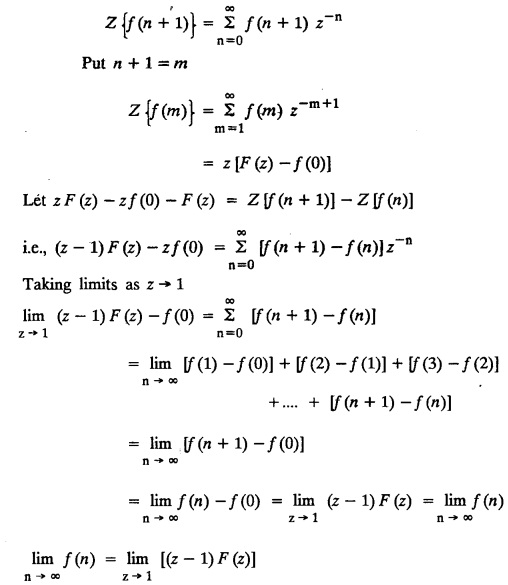
VIII. Problems based on initial value theorem and final value theorem
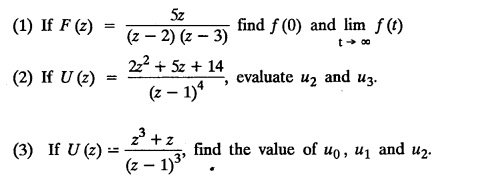
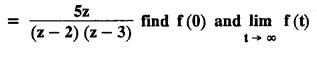
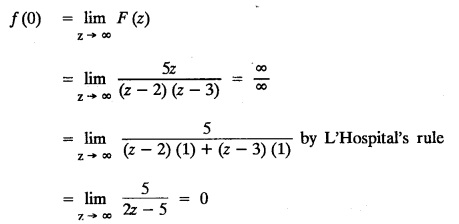
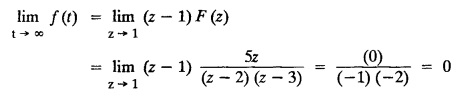
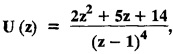 evaluate u2 and u3.
evaluate u2 and u3.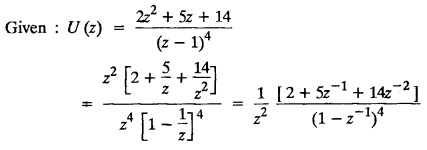
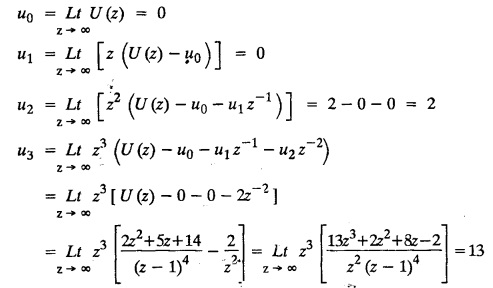
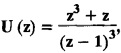 find the value of u0, u1 and u2.
find the value of u0, u1 and u2.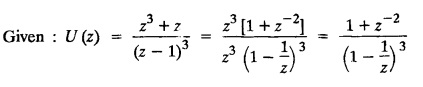
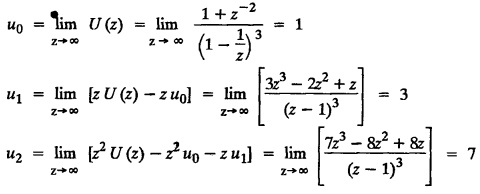
8. Differentiation :
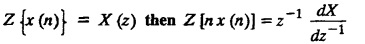
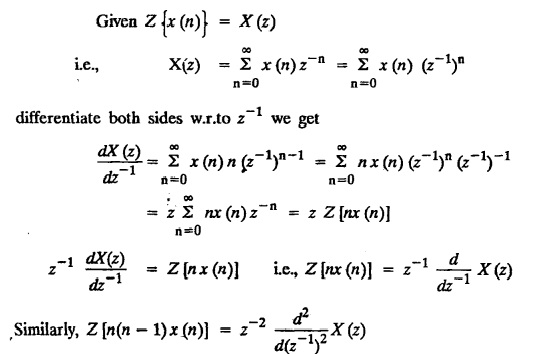
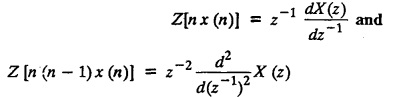

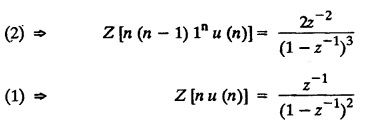
Transforms and Partial Differential Equations: Unit V: Z - Transforms and Difference Equations : Tag: : Applications, Elementary properties, Definition, Solved Example Problems - z - transforms
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
