Matrices and Calculus: Unit I: Matrices
Worked Examples of Real Quadratic Form Reduction to Canonical Form
Solved Example Problems
Worked Examples of Real Quadratic Form Reduction to Canonical Form : Example, Excercise with Answers : Matrices and Calculus: Matrices
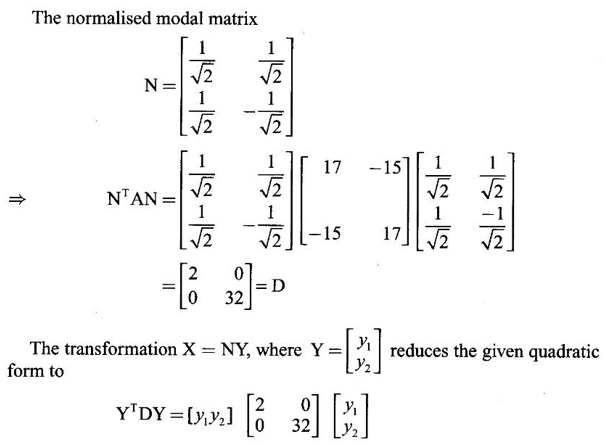
WORKED EXAMPLE Example 6 Write down the matrix of the quadratic form 2x12 − 2 x22 + 4 x32 + 2x1x2 − 6 x1x3 + 6 x2x3. Solution The Q.F is 2x12 − 2 x22 + 4 x32 + 2x1x2 − 6 x1x3 + 6 x2x3. It has 3 variables x1, x2, x3. So, the matrix of the quadratic form is a 3 × 3 symmetric matrix. Example 7 Write down the quadratic form corresponding to the matrix Solution Example 8 Determine the nature of the following quadratic form f(x1, x2, x3) = x12 + 2x22 Solution The given quadratic form in 3 variables x1, x2, x3 contains only square terms and so it is in canonical form. The coefficients are the eigen values. Here λ1 = 1, λ2 = 2, λ3 = 0, since there is no x32 term. ⸫ It is a positive semi-definite form. Example 9 Find the nature of the quadratic form 2x2 + 2xy + 3y2. Solution The given quadratic form is 2x2 + 2xy + 3y2 having 2 variables. So, the matrix of the quadratic form is A = The principal minors are D1 = 2 > 0 and D2 = ⸫ the quadratic form is positive definite. Example 10 Discuss the nature of the following quadratic forms. (i) 6x2 + 3y2 + 3z2 - 4xy - 2yz + 4zx (ii) 6x12+ 3x22 + 14x33 + 4x2x3 + 18x1x3 + 4x1x2 (iii) xy + yz + zx (iv) 10x2 + 2y2 + 5z2 + 6yz — 10zx – 4xy. Solution (i) The Q.F is 6x2 + 3y2 + 3z2 - 4xy - 2yz + 4zx, having 3 variables x, y, z. The matrix of the quadratic form is The principal minors are = 6(9 - 1) + 2(-6 + 2) +2(2 − 6) = 48 – 8 – 8 – 32 > 0 Since D1, D2, D3 are positive, the quadratic form is positive definite. (ii) The quadratic form is 6x12+ 3x22 + 14x33 + 4x2x3 + 18x1x3 + 4x1x2, having 3 variables x1, x2, x3. The matrix of the Q.F is The principal minors are = 6(42 − 4) – 2(28 − 18) + 9(4 – 27) =6(38) – 20 + 9 (-23) = 228 – 20 – 207 = 1 > 0 Since D1, D2, D3 are positive, the quadratic form is positive definite. (iii) The quadratic form is xy + yz + zx in 3 variables x, y, z The matrix of the quadratic form is A = Since D1 = 0, D2 < 0, D3 > 0, the quadratic form is indefinite. (iv) The Q.F 10x2 + 2y2 + 5z2 + 6yz — 10zx – 4xy is in three variables x, y, z. = 10 + 10 – 20 = 0 Since D1 > 0, D2 > 0 and D3 = 0, the quadratic form is positive semi-definite. Example 11 Determine λ so that λ (x2 + y2 + z2) + 2xy - 2yz + 2zx is positive definite. Solution The matrix of the quadratic form is A = The principal minors are D1 = λ Example 12 Show that the quadratic form ax12 −2bx1x2 + cx22 is positive definite if a > 0 and ac – b2 > 0. Solution The matrix of the quadratic form is A = The principal minors are D1 = a, D2 = |A| = Given a > 0 and ac – b2 > 0. ⸫ D1 > 0 and D2 > 0. Hence the Q.F is positive definite. Example 13 Find the index, signature and rank of the Q.F in 3 variables x12 + 2x22 − 3x32. Solution The quadratic form is in canonical form in 3 variables. ⸫ λ1 = 1, λ2 = 2, λ3 = −3. There are 2 positive eigen values. ⸫ Index = 2 One negative eigen value ⸫ signature = 2 – 1 = 1 Rank = 3 (i.e., the total number of +ve and -ve eigen values) Note Its nature is indefinite. Example 14 Reduce 6x2 + 3y2 + 3z2 - 4xy - 2yz + 4xz into a canonical form by an orthogonal reduction and find the rank, signature, index and the nature of the quadratic form. Solution Given quadratic form is 6x2 + 3y2 + 3z2 - 4xy - 2yz + 4xz The matrix of the Q.F is A = The characteristic equation is |A – λI| = 0 S3 = |A| = 6(9 − 1) + 2(−6 + 2) + 2(2 −6) = 48 - 8 – 8 = 32 ⸫ the characteristic equation is λ3 -12 λ2 + 36 λ - 32 = 0 By trial, λ = 2 is a root. ⸫ the eigen values are λ = 2, 2, 8 To find eigen vectors: Let X = Case (i) If λ = 8, then equations (I) become Case (ii) If λ= 2, then equations (I) become 4x1 - 2x2 + 2x3 = 0 ⇒ 2x1 - x2 + x3 = 0 -2x1 + x2 - x3 = 0 ⇒ 2x1 - x2 + x3 = 0 2x1 − x2 + x3 = 0 So we get only one equation 2x1 - x2 + x3 = 0 (1) Choosing x3 = 0, we get 2x1 - 2x2 = 0 ⇒ x2 = 2x1 Choosing x1 = 1, we get x2 = 2 ⸫ a + 2b = 0 ⇒ a = −2b Also X3 satisfies (1) ⸫ 2a – b + c = 0 ⇒ -4b – b + c = 0 ⇒ c = 5b Choosing b = 1 we get c = 5 and a = -2 Thus the eigen values are 8, 2, 2 and the corresponding eigen vectors are Clearly X3 is orthogonal to X1 and X2. But X1 and X2 are also orthogonal. The normalised eigen vectors are = 8y12 + 2y22 + 2y33, which is the canonical form. ⸫ rank of the Q.F = 3 Index = 3 Signature = 3 The Q.F is positive definite since all the eigen values are positive. Example 15 Reduce the quadratic form x12 + 5x22 + x32 + 2x1x2 + 2x2 x3 + 6 x3 x1 to canonical form through an orthogonal transformation. Solution The matrix of the quadratic form is A = The characteristic equation of A is │A – λI│= 0 S3 = |A| = 1·4 − (−2) + 3(−14) = 4 +2 −42 = −36 ⸫ the characteristic equation is λ3 − 7 λ2 + 36 = 0 By trial λ = -2 is a root. ⸫ the eigen values are λ = 2, 3, 6 To find eigen vectors: Let X = Case (i) If λ = -2, then the equations (I) become 3x1 + x2 + 3x3 = 0 x1 + 7x2 + x3 = 0 3x1 + x2 + 3x3 = 0 From first two equations, we get Case (ii) If λ = 3, then equations (I) become -2x1 + x2 + 3x3 = 0 x1 + 2x2 + x3 = 0 3x1 + x2 - 2x3 = 0 From the first two equations, we get Choosing x1= 1, x2 = −1, x3 = 1 we get an eigen vector X2 = Case (iii) If λ = 6, then equations (I) become -5x1 + x2 + 3x3 = 0 x1 - x2 + x3 = 0 3x1 + x2 - 5x3 = 0 From the first two equations, we get Since the eigen values are different, the eigen vectors are mutually orthogonal. Then = −2y12 + 3 y22 + 6 y32 which is the canonical form. Example 16 Reduce the quadratic form x2 + 5y2 + z2 + 2xy + 2yz + 6zx into canonical form and hence find its rank. Solution Refer the above Example 14 The eigen values are −2, 3, 6 ⸫ rank = 3 Example 17 Find out the type of conic represented by 17x2 - 30xy + 17y2 = 128 after reducing the quadratic form 17x2 - 30xy + 17y2 to canonical form by an orthogonal transformation. Solution Given quadratic form is 17x2 - 30xy + 17y2 The matrix of the Q.F is A = The characteristic equation of A is |A - λI| = 0 To find eigen vectors: Case (i) If λ = 2, then equations (I) become 15x4 −15x2 = 0 -15x1 + 15x2 = 0 ⇒ x1 = x2 Choosing x1 = 1, we get x2 = 1 ⸫ an eigen vector is Case (ii) If λ = 32, then equation (I) become 15x1 −15x2 = 0 -15x1 - 15x2 = 0 ⇒ x2 = -x1 Choose x1 = 1, we get x2 = -1 The normalised modal matrix = 2y12 + 32y22, which is the canonical form. But the given Q.F = 128 ⸫ 2y12 + 32y22 = 128 Example 18 Reduce the quadratic form 8x2 + 7y2 + 3z2 - 12xy + 4xz - 8yz to the canonical form by an orthogonal transformation. Find one set of values of x, y, z (not all zero) which will make the quadratic form zero. Solution Given quadratic form is 8x2 + 7y2 + 3z2 - 12xy + 4xz - 8yz The matrix of the quadratic form is A = The characteristic equation is |A - λI| = 0 ⇒ λ3 - S1 λ2 + S2 λ – S3 = 0 where S1 = 8 + 7 + 3 = 18 = (21 −16) + (24 − 4) + (56 − 36) = 5 + 20 + 20 = 45 S3 = |A| = 8(21 - 16) + 6(−18 + 8) + 2(24 − 14) = 40 – 60 + 20 = 0 ⸫ the characteristic equation is λ3 − 18 λ2 + 45λ = 0 ⇒ λ (λ2 -18 λ + 45) = 0 ⇒ λ (λ − 3)( λ − 15) = 0 ⇒ λ = 0,3,15 To find eigen vectors: If X = Case (i) If λ = 0, then the equations (I) become 8x1 − 6x2 + 2x3 = 0 ⇒ 4x1 − 3x2 + x3 = 0 -6x + 7x2 - 4x3 = 0 2x1 - 4x2 + 3x3 = 0 and y1, can take any value, we shall choose y1 = 3 ⸫ x = 1, y = 2, z = 2 Hence, this set of values will make the quadratic form = 0 Example 19 Reduce the quadratic form 2x12 + 6x22 + 2x32 + 8x1x3 to canonical form. Solution The quadratic form is 2x12 + 6x22 + 2x32 + 8x1x3 ⸫ the matrix of the quadratic form is A = The characteristic equation of A is │A - λI│= 0 = 12 + (4 - 16) + 12 = 12 S3 = |A| = 2(12) + 4(−24) = −72 ⸫ Characteristic equation is λ3 - 10 λ2 + 12 λ + 72 = 0 By trial we find λ = -2 is a root ⸫ the eigen values are λ = -2, 6, 6 To find eigen vectors: If X = Then (A - λ I)X = 0 Case (i) If λ = -2, then the equations (I) become 4x1 + 4x3 = 0 ⇒ x1 + x3 = 0 ⇒ x3 = -x1 8 x2 = 0 ⇒ x2 = 0 Taking x1 = 1, we get x3 = -1 ⸫ an eigen vector is Case (ii) If λ = 6, then equations (I) become -4x1 + 4x3 = 0 ⇒ x1 = x3 and 0x2 = 0 ⇒ x2 can take any value. If x1 = 1, then x3 = 1. Choose x2 = 0 ⸫ an eigen vector is We shall choose an eigen vector X3 orthogonal to X2 Since the canonical form has positive and negative terms, the quadratic form is indefinite in nature. Example 20 Reduce the given quadratic form Q to its canonical form using orthogonal transformation Q = x2 + 3y2 + 3z2 – 2yz. Solution Given quadratic form is Q = x2 + 3y2 + 3z2 – 2yz The matrix of the quadratic form is A = The characteristic equation is |A-λI | = 0 To find eigen vectors: Let X = Case (i) If λ = 1, then equations (I) become 0x1 + 0x2 + x3 = 0 ⇒ x3 = 0 0x1 + 2x2 - x3 = 0 ⇒ 2x2 = x3 0x1 - x2 + 2x3 = 0 ⇒ 2x2 = 2x3 x3 = 0 ⇒ x2 = 0 x1 can be any real value. We shall take x1 = 1 ⸫ an eigen vector is Case (ii) If λ = 2, then the equations (I) become -x1 = 0 ⇒ x1 = 0 0x1 + x2 - x3 = 0 ⇒ x2 = x3 0x1 - x2 + x3 = 0 ⇒ x2 = x3 Take x2 = 1 ⸫ x2 = 1 ⸫ an eigen vector is Case (iii) If λ = 4, then the equations (I) become -3x1 + 0x2 + 0x3 = 0 ⇒ x1 = 0 0x1 - x2 - x3 = 0 ⇒ x2 = -x3 0x1 - x2 - x3 = 0 ⇒ x2 = -x3 Take x2 = 1 ⸫ x2 = 1 ⸫ an eigen vector is Thus the eigen values are λ= 1,2,4 and the corresponding eigen vectors are The orthogonal transformation X = NY, where Y = which is the canonical form. Example 21 Reduce the quadratic form x12 + 2x22 + x33 − 2x1x2 + 2x2x3 to the canonical form through an orthogonal transformation and hence show that it is positive semi-definite. Also give a non-zero set of values (x1, x2, x3) which makes the quadratic form zero. Solution Given the quadratic form is x12 + 2x22 + x33 − 2x1x2 + 2x2x3 The matrix of the quadratic form is A = The characteristic equation of A is |A - λI| = 0 To find eigen vectors: If ⇒ (1 − λ)x1 – x2 + 0 x3 = 0 − x1 + (2− λ) x2 + x3 = 0 (I) 0x1 + x2 +(1− λ)x3 = 0 Case (i) If λ = 0, then the equations (I) become x1 - x2 = 0 ⇒ x1 = x2 -x1 + 2x2 + x3 x2 + x3 = 0 ⇒ x3 = -x2 Take x2 = 1, then x1 = 1, x3 = −1 ⸫ an eigen vector is Case (ii) If λ = 1, the equations (I) become 0x1 - x2 = 0 ⇒ x2 = 0 -x1 + x2 + x3 = 0 ⇒ x1 = x3 Take x3 = 1 ⸫ an eigen vector is X2 = Case (iii) If λ = 3, then equations (I) become -2x1 - x2 = 0 ⇒ x2 = -2x1 -x1 - x2 + x3 = 0 x2 -2x3 = 0 ⇒ x2 = 2x3 Take x2 = 2, then x1 = -1, x3 = 1 ⸫ an eigen vector is X3 = Thus the eigen values are λ = 0, 1, 3 and the eigen vectors are The orthogonal transformation is X = NY These equation make the quadratic form = 0 ⇒ y22 + 3y32 = 0 ⇒ y2 = 0 and y3 = 0 [Since sum of squares of real numbers = 0 ⇒ each number = 0] and y1 can take any real value. EXERCISE 1.3 1. Diagonalise 2. Reduce the matrix 3. Reduce 4. Reduce A = 5. Diagonalise 6. Find the symmetric matrix A whose eigen values and eigen vectors are given (i) eigen values are 0, 2, and eigen vectors (ii) eigen values are 1, 2, 3 and eigen vectors 7. Reduce the quadratic form 8x12 + 7x22 + 3x32 −12x1x2 − 8 x2x3 + 4x3x1 to the canonical form through an orthogonal transformation and hence show that it is positive semi-definite. 8. Reduce the quadratic form 2x12 + 6x22 + 2x32 − 8x1x3 to canonical form by orthogonal reduction. 9. Reduce the quadratic form 3x12 + 5x22 + 3x32 −2x2x3 + 2x3x1 - 2x1x2 to the canonical form by orthogonal reduction. 10. Find the nature, index, signature and rank of the following Q.F, without reducing to canonical form. (i) 3x12 + 5x22 + 3x32 −2x2x3 + 2x3x1 - 2x1x2 (ii) 10x2 +2y2 + 5z2 + 6yz - 10zx – 4xy. (iii) 3x2- 2y2 - z2 - 4xy + 8xz +12yz. 11. Express the quadratic form 6x2 + 3y2 + 3z2 + 2yz + 4zx - 4xy into a sum of squares. 12. Reduce x12 + 3x22 + 3x32 + 2x2x3 to canonical form ANSWERS TO EXEECISE 1.3 1. λ = 2, 2, 8; eigen vectors [0 1 1]T, [1 1 -1]T, [2 −1 1]T 2. λ = 0, 3, 14; eigen vectors [1 -5 4]T, [1 1 1]T, [−3 1 2]T 3. λ = 0, 3, 15; eigen vectors [1 2 2]T, [2 1 −2]T, [2 −2 1]T 4. λ = 1, 1, 4; eigen vectors [1 1 0]T, [−1 1 2]T, [1 −1 1]T 5. λ = 3, 6, 9; eigen vectors [1 2 2]T, [2 1 −2]T, [2 −2 1]T 6. (i) A = 7. 3y22 + 15y32 8. −2y12 + 6y22 +6y32 9. 2 y12 + 3 y22 + 6 y32 10. (i) Eigen values are 2, 3, 6; positive definite, index = 3, signature rank = 3. (ii) Eigen values are Q, 3, 14; positive semi-definite, index = 2, signature = 2, rank = 2. (iii) Eigen values are 3, 6, -9; indefinite, index = 2, signature 1, rank = 3. 11. 4x2 + y2 + z2 12. y12 + 2y22 + 4y32


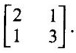
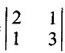 = 5 > 0
= 5 > 0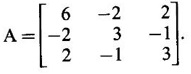


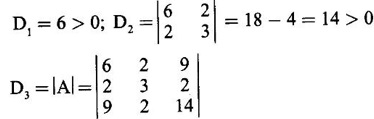


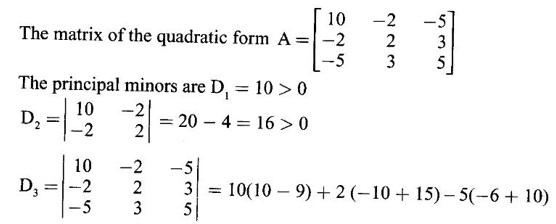



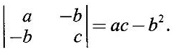



![]() be an eigen vector corresponding to eigen value λ.
be an eigen vector corresponding to eigen value λ.
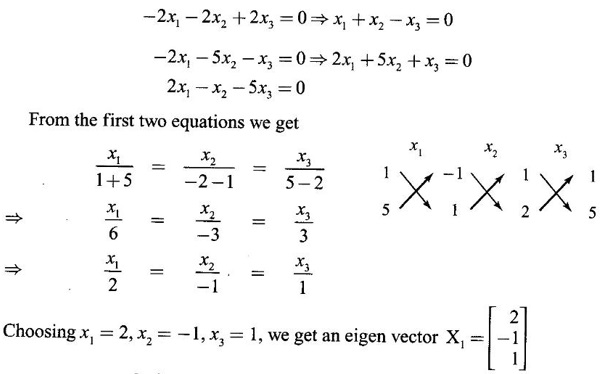


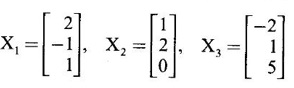





![]() be an eigen vector corresponding to eigen value λ.
be an eigen vector corresponding to eigen value λ.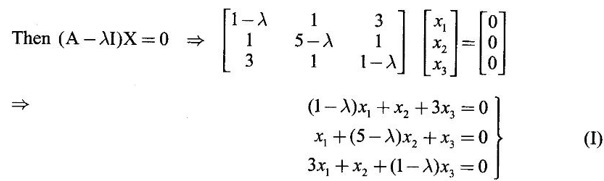
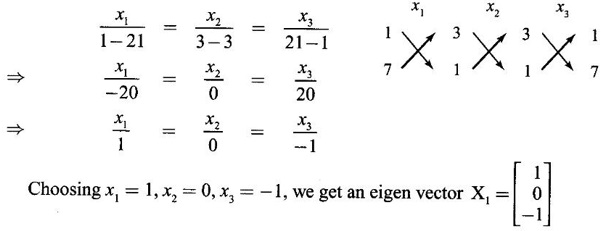
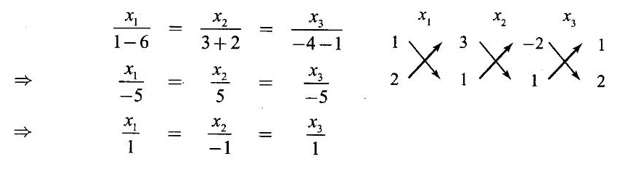




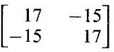
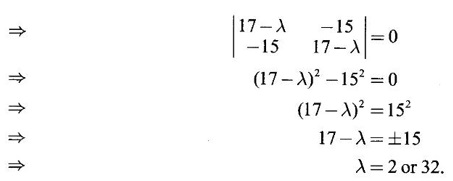

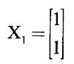

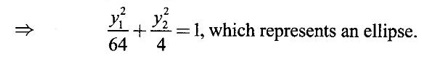
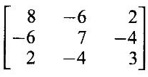
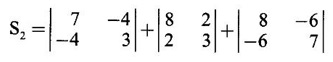
![]() be an eigen vector of the eigen value λ of A, then
be an eigen vector of the eigen value λ of A, then




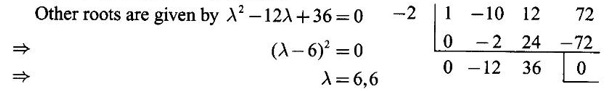
![]() be an eigen vector corresponding to the eigen value λ of A.
be an eigen vector corresponding to the eigen value λ of A.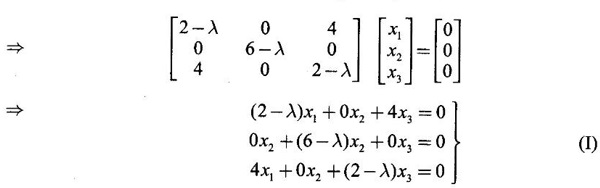

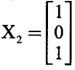

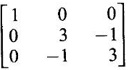

![]() be an eigen vector corresponding to an eigen value λ of A.
be an eigen vector corresponding to an eigen value λ of A.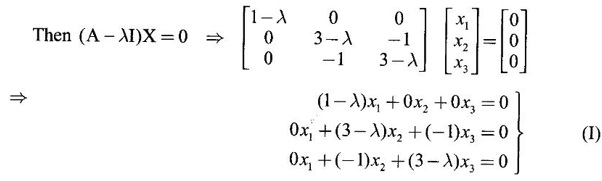
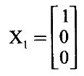
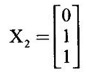
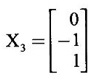

![]() reduces the given quadratic form to
reduces the given quadratic form to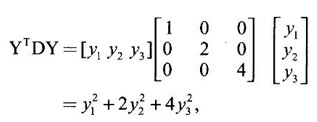


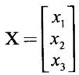 be an eigen vector corresponding to an eigen value λ of A, then
be an eigen vector corresponding to an eigen value λ of A, then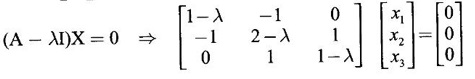
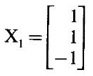
![]()
![]()


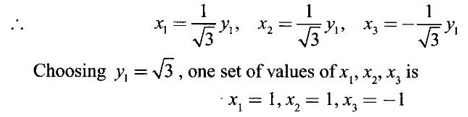
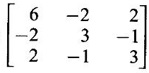 by an orthogonal transformation.
by an orthogonal transformation. to diagonal form.
to diagonal form. to diagonal form by orthogonal reduction.
to diagonal form by orthogonal reduction. to diagonal form by orthogonal reduction. Hence find A3.
to diagonal form by orthogonal reduction. Hence find A3.
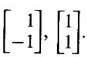


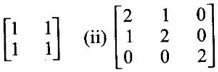
Matrices and Calculus: Unit I: Matrices : Tag: : Solved Example Problems - Worked Examples of Real Quadratic Form Reduction to Canonical Form
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
