Matrices and Calculus: Unit I: Matrices
Worked Examples of Application of Eigen Value Problem: Stretching of an Elastic Membrane
Worked Examples : Example, Excercise with Answers : Matrices and Calculus: Matrices
WORKED EXAMPLES Example 1 An elastic membrane in the xy-plane with boundary the circle x2 + y2 is stretched so that a point P(x1, x2) moves to the point Q(y1, y2) by the deformation Y = AX where A = Solution Given the transformation We want to find the principal directions of stretch. That is, we want to find vectors X such that Y = λX (1) Since Y = AX, we have AX = λX This means λ is an eigen value of A. So, we shall find the eigen values and eigen vectors of A. The characteristic equation of A is If λ = 2, then the equations (I) become From (1) we have Y1 = 8X1 and Y2 = 2X2 ⸫ Vector Y1 has the same direction as X1 and vector Y2 has the same direction as X2. Hence they give the principal directions. X1 is the position vector of the point P1(1, 1) and X2 is the position vector of the point P2 (1, −1). Slope of OP1 is tan θ = 1 ⇒ θ = 45° Slope of OP2 is tan θ = -1 ⇒ θ = 135° ⸫ the vectors X1 and X2 make angles 45°, 135°, with the positive direction of the x-axis. These give the principal directions and angle between them is 90°. So, X1 and X2 are perpendicular vectors. Since Y1 = 8 X1 and Y2 = 2X2 , we find the membrane is stretched by the factors 8 and 2 in the principal directions of stretch. (ii) Since the principal directions are perpendicular to each other, we can choose them as directions of a new Cartesian coordinate system, say u1 u2 - coordinate system with positive u1 - axis in the I quadrant and positive u2 - axis in the II quadrant of the xy-system. The polar coordinates of a point in the new system are u1 = r cos φ u2 = r sin φ ⸫ the coordinates of a point on the boundary circle x2 + y2 = 1 are (cos φ , sin φ) [⸪ r = 1] Hence after the stretch in the principal directions we have which is an ellipse with semi major axis 8 and semi-minor axis 2. We shall show the boundary circle and the deformed membrane in the same figure. The boundary circle of the membrane and the deformed ellipse. Note The deformed ellipse is the canonical form of the quadratic form (4) in example 2. A formula: The slope of the line joining the points (x1, y1) and (x2, y2) is If this line makes an angle θ with the positive direction of the x-axis, the angle θ is measured from the positive x-axis towards the line in the anticlockwise sense, then slope of the line is tan θ Thus Example 2 Given the elastic deformation Y = Solution Given the transformation Y = We want to find the principal directions of stretch. That is we want to find vectors X such that Y = λX So, we find the eigen values and eigen vectors of A. The characteristic equation is If λ = 4.5, then the equations (I) become If x1 = 1, then x2 = -1. ⸫ an eigen vector corresponding to λ = 4.5 is If λ = 1.5, then the equations(I) become So, we have Y1 = 4.5 X1 and Y2 = 1.5 X2, which give the principal directions of the shift. X1 is the position vector of P1 (1, 1) and X2 is the position vector of P2 (1, −1). Slope of OP1 is tan θ = 1 ⇒ θ = 45° Slope of OP2 is tan θ = -1 ⇒ θ = 135° ⸫ the vectors X1 and X2 make angles 45°, 135° with the positive direction of the x-axis. They give the principal directions and the angle between them is 90°. So, the principal directions are perpendicular to each other. Since Y1 = 4.5 X1 and Y2 = 1.5 X2, the factors of extension are 4.5 and 1.5 Example 3 Given the elastic deformation Y = AX, where A = Solution Given the deformation Y= AX where A = We want to find the shift of X to Y in the principal directions. That is we want to find vectors X such that Y = λX (1) ⸫ AX = λX So, we find the eigen values and eigen vectors of A. If x2 = 1, then x1 = √6, ⸫ an eigen vector corresponding to λ = 8 is X2 = So, we have Y1 = X1 and Y2 = 8X2, which give the principal directions. If X1 is the position vector of the point P1(1,−√6), then slope of OP1 = - √6 = m1 and tan θ = −√6 ⇒ θ =112.2°. If X2 is the position vector of the point P2 (√6,1), the slope of the slope of OP2 = ⸫ m1m2 = -1 So, X1 and X2 are perpendicular to each other making angles 112.21° and 22.21° with positive x-axis. These give the principal directions of shift. The factors of extension are 1 and 8. EXERCISE 1.4 Find the principal directions and corresponding factors of extension or contraction of the elastic deformation. Y=AX were A is given below ANSWERS TO EXERCISE 1.4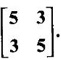 Find the principal directions of stretch and the shape of the boundary circle changes under this deformation.
Find the principal directions of stretch and the shape of the boundary circle changes under this deformation.

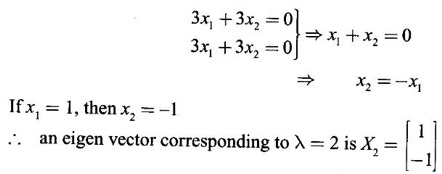

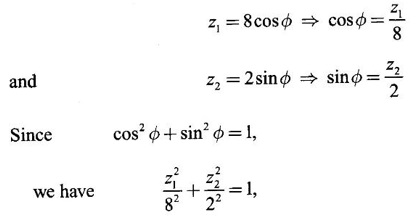



 find the principal directions and the factors of extension or contraction with details.
find the principal directions and the factors of extension or contraction with details.
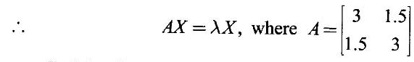
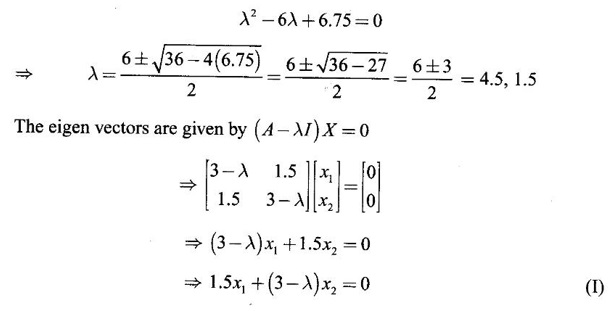
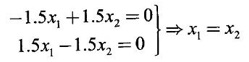
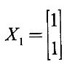


 find the principal directions and corresponding factors of extension or contraction with details.
find the principal directions and corresponding factors of extension or contraction with details.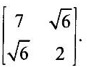

![]()



Matrices and Calculus: Unit I: Matrices : Tag: : - Worked Examples of Application of Eigen Value Problem: Stretching of an Elastic Membrane
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
