Theory of Machines: Unit I: Kinematics of Mechanisms
velocity analysis by relative velocity method
relative velocity of two bodies
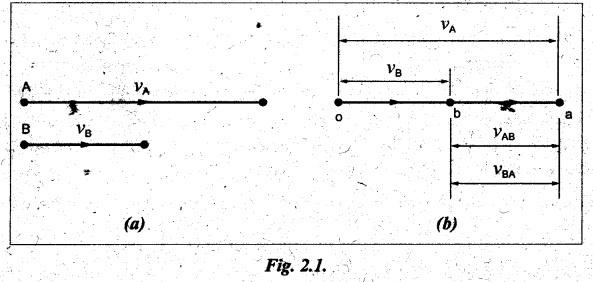
Consider two bodies A and B moving along parallel lines in the same direction with absolute velocities vA and vB, as shown in Fig.2.1(a).
VELOCITY ANALYSIS BY RELATIVE VELOCITY METHOD
RELATIVE VELOCITY OF TWO BODIES
1. Relative Velocity of Two Bodies Moving along Parallel Lines
Consider
two bodies A and B moving along parallel lines in the same direction with
absolute velocities vA and vB, as shown in
Fig.2.1(a).
Then
the relative velocity of A with respect to B (Fig.2.1(b)) is given by
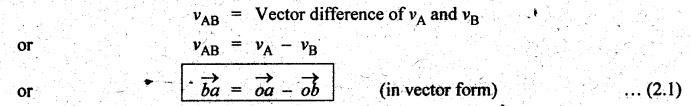
Similarly,
the relative velocity of B with respect to A is given by

2. Relative Velocity of Two Bodies Moving along Inclined Lines
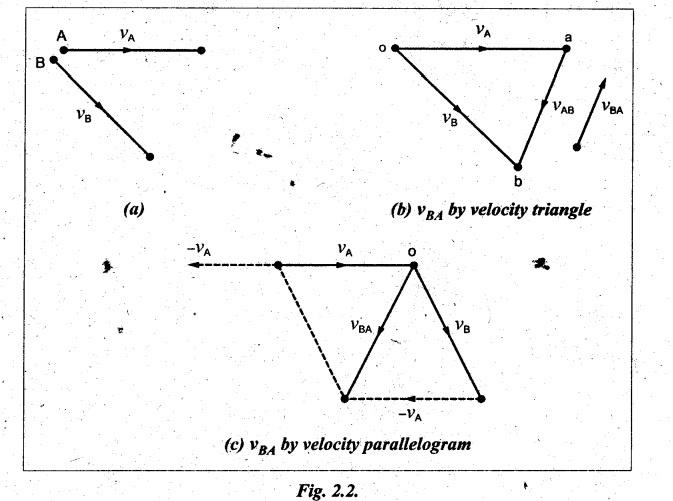
Now
consider the two bodies A and B moving with absolute velocities V and v ̧, as
shown in Fig.2.2(a). Then the relative velocity of A (or B) with respect to B
(or A) may be obtained by (a) the triangle law of velocities or (b) the law of
parallelogram of velocities.
(a)
vAB by velocity triangle (Fig.2.2(b)): Take any fixed
point o representing zero velocity point. From point o, draw vector oa parallel
to v and draw vector ob parallel to v to some suitable scale. Then join ab to
get the velocity triangle abc. The vector ab represents the relative velocity
of B with respect to A (vBA).
The
relative velocity of A with respect to B (Fig.2.2(b)) is given by
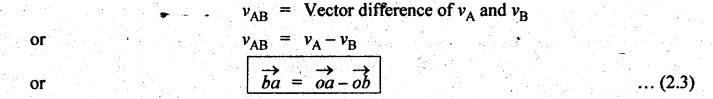
Similarly,
the velocity of B with respect A is given by
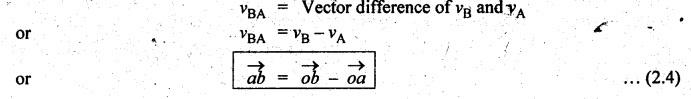
(b)
vBA by velocity parallelogram (Fig.2.2(c));
Let – vA velocity is given to both particles A and B as shown
in Fig.2.2(c). When - VA is added to both particles, then particle A comes to
rest; but there is no change in their relative velocity. Now the relative velocity
of B with respect to A (vBA) can be determined by drawing the
parallelogram as shown in Fig.2.2(c).
vBA = vB - vA
Note
1.
When we simply say, velocity of particle A, it refers to the absolute velocity
of A (vA)
i.e.,
the velocity with respect to a fixed point O (vAO). So vA
= vAO.
2.
The relative velocity of point A with respect to B (vAB) and
the relative velocity of point B with respect to A (vBA) are
equal in magnitude but opposite in direction.

Theory of Machines: Unit I: Kinematics of Mechanisms : Tag: : relative velocity of two bodies - velocity analysis by relative velocity method
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
