velocity analysis by instantaneous centre method

III. VELOCITY ANALYSIS BY INSTANTANEOUS CENTRE METHOD

INSTANTANEOUS CENTRE OF ROTATION

Concept:

• The combined motion of rotation and translation of a link in the mechanism may be assumed to be a motion of pure rotation about some centre I, known as the instantaneous centre of rotation or virtual centre of rotation.

• Illustration: In many cases, a body has simultaneously a motion of rotation as well as translation. For example, the wheels of a car moving on road surface have rotary as well as translatory motion.

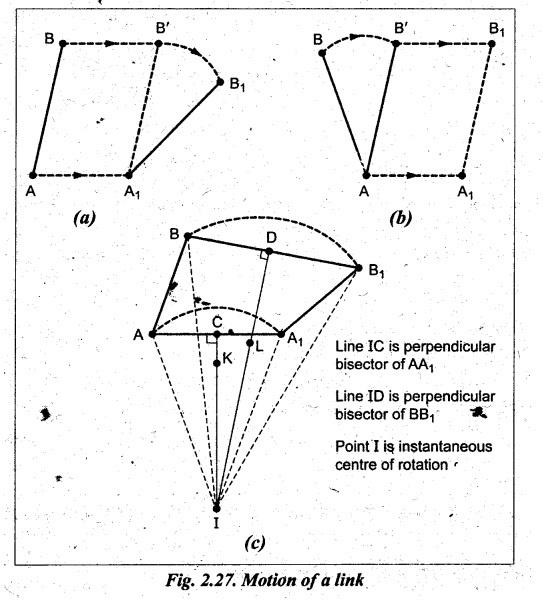
Consider a rigid link AB which moves from its initial position AB to A₁B₁ as shown in Fig.2.27(a). AB has reached to A₁B' position through translatory and from A₁B' to A₁B₁ through rotary motion. In Fig.2.27(b), the link AB has first the motion of rotation from AB to AB' about A and then the motion of translation from AB′ to A₁B₁. Thus A₁B₁ which is the final position of AB, is the combined effect to translatory and rotary motions.

This combined motion of rotation and translation of the link AB may be assumed to be a motion of pure rotation about some centre I, known as the instantaneous centre of rotation.

• Location of position of instantáneous centre: The position of instantaneous centre may be located as discussed below:

Refer Fig.2.27(c), join A to A₁ and B to B₁. Draw perpendicular bisectors from AA₁ and BB₁ to intersect at point I. When the point A of the rigid link moves from A to A₁ position, it is assumed that the rotary motion takes place about point K on the bisector of CK. Similarly, when B moves to B₁, the rotary motion can be expected about any point L on the bisector DL. As the bisector intersect at point I, it is the point about which the link rotates. Point I is known as the instantaneous centre of rotation.

• The position of instantaneous centre changes with the changed position of the link AB. There will be different instantaneous centres for different positions of link AB.

VELOCITY OF A POINT ON A LINK BY INSTANTANEOUS CENTRE METHOD

✓ Consider a link AB shown in Fig.2.28. Let VA and vg be the absolute velocities of points A and B on the link.

Let us assume that both the magnitude and velocity of point A is known, while the direction of velocity of point B only is known (but magnitude is unknown).

The instantaneous centre of I of the link AB at this instant can be located by drawing perpendiculars to the directions of VA and vg, as shown in Fig.2.28. The intersecting point is the required instantaneous centre I.

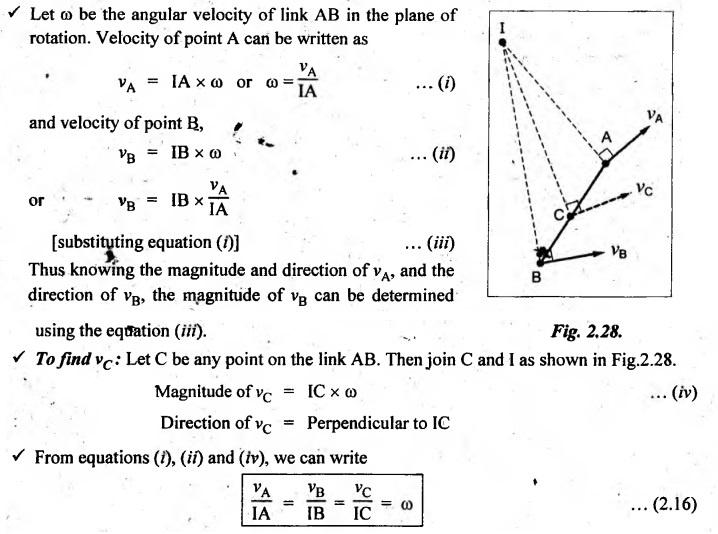
From equation (2.16), it can be stated that the magnitudes of the velocities of the points on a link is directly proportional to their distance from the instantaneous centre. The direction of their velocities is perpendicular to the line joining them with the instantaneous centre.

NUMBER OF INSTANTANEOUS CENTRES IN A MECHANISM

• It may be noted that there will be one instantaneous centre for two links having relative motion between them. Therefore, the number of instantaneous centres in a mechanism having n links will be equal to possible pairs of two links taken at a point.

• Mathematically, the number of instantaneous centres (N) in a mechanism is given by

where

n = Number of links