Theory of Machines: Unit III: Friction in Machine Elements
V-belt. Drive
Friction in Machine Elements - Theory of Machines
When a belt is trapezoidal in section, designed to run in a V-shaped groove, it is known as a V-belt.
V-BELT DRIVE • When a belt is trapezoidal in section, designed to run in a V-shaped groove, it is known as a V-belt. • An alternate way of increasing the ratio of tension is the use of V-grooved pulley. • V-belt drive is particularly suitable when the shafts are at a short distance apart. • The V-belts are made of fabric and cords moulded in rubber and covered with fabric and rubber, as shown in Fig.8.24. • The included angle for the V-belt is usually from 30° - 40°. Advantages of V-belt drive 1. Power transmitted is more due to wedging action in the grooved-pulleys. 2. V-belt is more compact, quiet and shock absorbing. 3. The V-belt drive is positive because of negligible slip between the belt and the groove. 4. High velocity'ratio (maximum 10) may be obtained. 5. Strength of material of the V-belt is more efficiently utilised for a given power transmission. 6. Multiple V-belts can be used, thus enabling transmission of more power. Disadvantages of V-belt drive 1. It cannot be used with large centre distances. 2. It is not as durable as flat belt. 3. Since the V-belt is subjected to certain amount of creep, therefore it is not suitable for constant speed application such as synchronous machines, and timing devices. The limiting tension ratio for V-belt drive is given by where T1 = Tension in the tight side in newtons, T2 = Tension in the slack side in newtons, 2 β = Angle of the groove, and μ = Coefficient of friction between the belt and sides of the groove. Note 1. The number of V-belts required can be determined using the following relation. 2. The value of groove angle (28) for flat belt drive = 180°. Substituting 2β = 180° for flat belt drive, we get the same tension ratio equation i.e., T1/T2 = eμθ. Example 8.13 A compressor requires 90 kW to operate at 250 rpm. The drive is by V-belts from an electric motor running at 750 rpm. The diameter of the pulley on the compressor shaft must not be greater than 1 metres while the centre distance between the pulleys is limited to 1.75 m. The belt speed should not exceed 1600 m/min. Determine the number of V-belts required to transmit the power if each belt has a cross-sectional area of 375 mm2, density 1000 kg/m3 and an allowable tensile stress of 2.5 MPa. The groove angle of the pulley is 35o. The coefficient of friction between the belt and the pulley is 0.25. Also calculate the length required for each belt. Given data: P = 90 kW = 90 × 103 W; Driver pulley = Motor pulley; Driven pulley = Compressor pulley; N2 = 250 rpm; N1 = 750 rpm; d2 = 1 m; x = 1.75 m; v = 1600 m/min = 1600/60 = 26.67 m/s; α = 375 mm2 = 375 × 10-6 m2; ρ = 1000 kg/m3; σ = 2.5 MPa = 2.5 × 106 N/m2; 2 β = 35° or β = 17.5°; μ = 0.25. Solution: We know that mass of the belt per metre length, m = Area × Length × Density = 375 × 10-6 × 1 × 1000 = 0.375 kg ⸫ Centrifugal tension, TC = m • v2 = 0.375 (26.67)2 = 266.7 N and maximum tension in the belt, Tmax = σ • α = (2.5 × 106) (375 × 10-6) = 937.5 N ⸫ Tension in the tight side of the belt, We know that tension ratio of V-belt drive, Number of V-belts required: We know that power transmitted per belt, Length required for each belt: We know that length of belt for an open belt drive,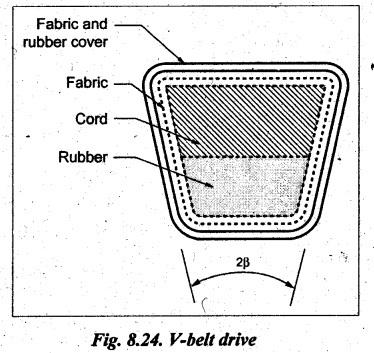
1. Advantages and Disadvantages of V-belt Drive (over Flat Belt Drive)
2. Ratio of Driving Tensions for V-belt


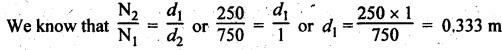
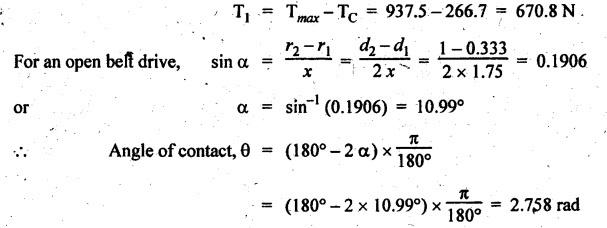
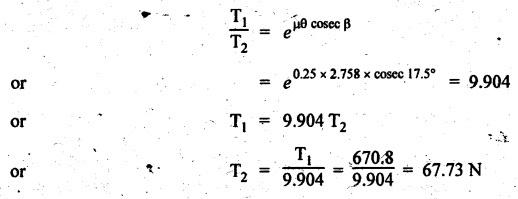
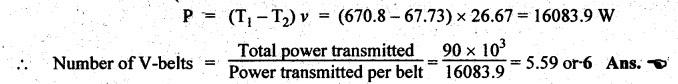
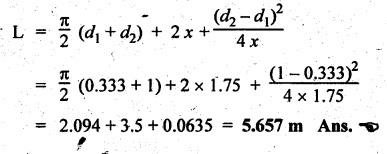
Theory of Machines: Unit III: Friction in Machine Elements : Tag: : Friction in Machine Elements - Theory of Machines - V-belt. Drive
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
