Engineering Thermodynamics: Unit III: Availability and Applications of II Law
Useful work based on the second law of thermodynamics for non-flow processes
Consider a system having initial and final boundaries with volume of V1 and V2. The surrounding is with the atmospheric pressure of p0 and temperature of T0.
USEFUL WORK BASED ON THE SECOND LAW OF THERMODYNAMICS FOR NON-FLOW PROCESSES Consider a system having initial and final boundaries with volume of V1 and V2. The surrounding is with the atmospheric pressure of p0 and temperature of T0. where Wact be the maximum work of the system or process Wact = Wmax = Q - ΔU = To ΔS – ΔU ……(3.29) [⸪ Q = To ΔS for reversible process] = To (S2 - S1) - (U2 - U1) ... (3.30) Substituting equation (3.30) in (3.28), ⸫ Maximum useful work, (Wu)max = To (S2 - S1) - (U2 - U1) - po (V2 - V1) = (U1 - U2) + po (V1 – V2) - To (S1 – S2) = (U1 - U2) + To (S2 - S1) + po (V1 – V2) (Wu)max = (U1 + poV1 - ToS1) - (U2 + poV2 - ToS2) Also, the maximum useful is equal to the change in availability, (Wu)max = ϕ1 – ϕ2 Change in availability, ϕ1 – ϕ2 = (Wu)max = (U1 - U2) + To (S2 - S1) + po (V1 – V2) = Wmax + po (V1 – V2) where ϕ be the availability function for a closed system. It is given by ϕ = U + po V - To S For unit mass, the useful work becomes, (Wu)max = (U1 + poV1 - ToS1) - (u2 + pov2 - Tos2) In addition to the atmosphere, the system exchanges heat with a thermal energy reservoir at a temperature of Tr. So, the maximum useful work increases. As per Carnot principle,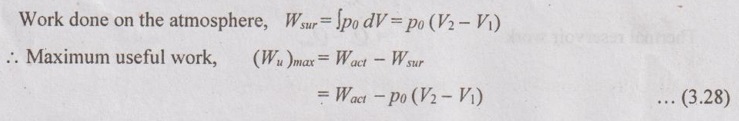

Engineering Thermodynamics: Unit III: Availability and Applications of II Law : Tag: : - Useful work based on the second law of thermodynamics for non-flow processes
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
