Strength of Materials: Unit II: Transverse Loading on Beams and Stresses in Beam
university solved problems on overhanging beam
Transverse Loading on Beams and Stresses in Beam - Strength of Materials
university solved problems on overhanging beam: Transverse Loading on Beams and Stresses in Beam - Strength of Materials
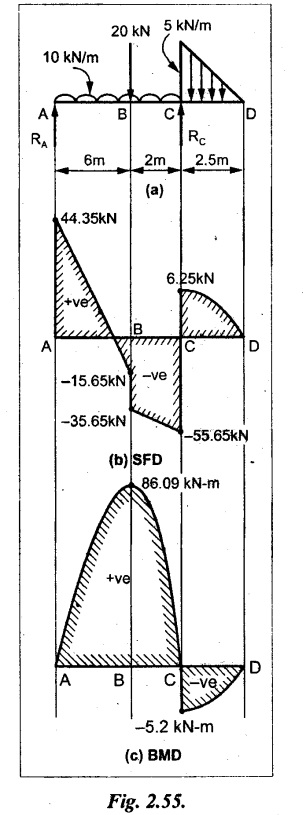
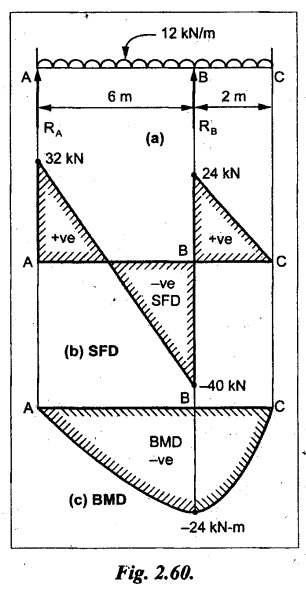
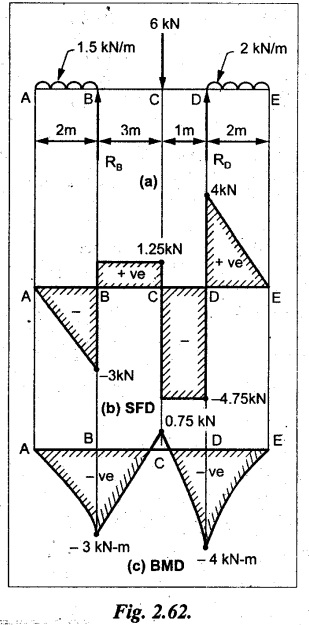
UNIVERSITY SOLVED PROBLEMS ON OVERHANGING BEAM Example 2.42: Draw the shear force and bending moment diagrams for the beam shown in Fig. 2.55(a) indicating principle values. Given: As shown in Fig.2.55(a). To draw: SFD and BMD Solution: Taking moment about A, SF calculation: SF at D = 0 SF at C (without reaction RC) SF at C (with reaction RC) = 6.25 - RC = 6.25 - 61.9 = - 55.65 kN SF at B (without point load) = −55.65 + 10 × 2 = - 35.65 kN SF at B (with point load) = -35.65 + 20 = 15.65 kN SF at A = RA = 44.35 kN Join the values CD by parabolic curve and all other values by inclined straight lines as shown in Fig.2.55(b). BM calculation: BM at D = 0 BM at A = 0 Join all the values AB and C by parabolic curves and CD by a cubic curves as shown in Fig.2.55(c). Result: The SFD and BMD are shown in Fig.2.55(b) & (c) respectively. Example 2.43: Draw the shear force and bending moment diagrams for the beam loaded as shown, locate the point of contraflexure and find the maximum and minimum values of BM. Given: As shown in Fig.2.56(a). To find: (i) Draw SFD and BMD. (ii) Find the maximum and minimum of BM. Solution: Taking moment about B, RC = 33.375 kN RB + RC = 6 × 13 = 78 kN RB = 78 - 33.375 = 44.625 kN SF calculation: SF at D = 0 SF at C (without reaction RC) = 6 × 2 = 12 kN SF at C (with reaction RC) = 6 × 2 -33.375 = -21.375 kN SF at B (without reaction RB) = 6 × 10 - 33.375 = 26.625 kN SF at B (with reaction RB) = 6 × 10 - 33.375 - 44.625 = -18 kN SF at A = 6 × 13 - 33.375 - 44.625 = 0 Join all the values as shown in Fig.2.56(b). BM calculation: BM at D = 0 BM at A = 0 Maximum BM calculation: Taking the SF at a distance 'x' m from D. SFx = 6 × x - 33.375 = 0 x = 5.5625 m from D Maximum BM: Join all the values by parabolic curves as shown in Fig.2.56(c). Result: The SFD and BMD are shown in Fig.2.56(b) & (c) respectively. Minimum value of BM = 0 Maximum value of BM = 26.07 kN-m Example 2.44: Draw the SF and BM diagrams for the beam shown below, Find the maximum values and their positions. Give the values at important points in the diagram. Given: As shown in Fig.2.57(a). To draw: (i) SFD and BMD (ii) Maximum BM Solution: Taking moment about A, RA + RB = 2 × 6 + 2 = 14 kN RA = 14 - RB = 14 - RB = 14 - 12 = 2 kN SF calculation SF at C = 2 kN SF at B (without Reaction RB) = 2 +2 × 2 = 6 kN SF at B (with Reaction RB) = 6 - RB = 6 – 12 = -6 kN SF at A = RA = 2 kN Join all the values as shown in Fig.2.57(b). BM calculation: BM at C = 0 BM at A = 0 Maximum BM calculation: Taking SF at a distance 'x' m from C SFx = 2 – 12 + 2 × x = 0 -10 + 2 x = 0 ⇒ 2x = 10 x = 5 m from C Maximum BM: Join all BM values as shown in Fig.2.57(c). Result: The SFD and BMD are shown in Fig.2.57(b) & (c) respectively. The maximum BM 1 KN-m occurs at a distance of 5 m from end C. Example 2.45: Draw the shear force and bending moment diagram for the loaded beam shown in Fig.2.58(a). Given: As shown in Fig.2.58(a). To draw: SFD and BMD Solution: Taking moment about A, = 56.875 kN SF calculation: SF at D = 0 SF at B (without reaction RB) = 10 × 3 = 30 kN SF at B (with reaction RB) = 30 - 73.125 = - 43.125 kN SF at A (without reaction RA) = 10 × 11 - 73.125 = 36.875 kN SF at A (with reaction RA) = 36.875 - 56.875 = - 20 kN SF at C = 0 Join all the values as shown in Fig.2.58(b). BM calculation: BM at D = 0 BM at C = 0 Maximum BM calculation: SF equation where it changes sign. (i.e., x m from the end D), SFx = 10 × x - RB 10 × x - 73.125 = 0 x = 7.3125 m Therefore, = 47.988 KN-m Join all the BM values as shown in Fig.2.58(c). Result: The SFD and BMD are shown in Fig.2.58(b) & (c). Example 2.46: A beam 6m long rests on supports 5m apart, the right hand end is overhanging by Im. The beam carries a UDL of 20 kN/m over the entire length of the beam. Draw SFD and BMD indicating the maximum BM and the point of contraflexure. Given: As shown in Fig.2.59(a). To draw: (i) SFD and BMD (ii) Mmax and Point of contraflexure Solution: Taking moment about A, RA + RB = 20 × 6 = 120 kN RA = 120 - RB = 120 - 72 = 48 kN SF calculation: SF at C = 0 SF at B (without reaction RB) = 20 × 1 = 20 kN SF at B (with reaction RB) = 20 – 72 = -52 kN SF at A = RA = 48 kN Join all the values as shown in Fig.2.59(b). BM calculation: BM at C = 0 BM at A = 0 Maximum BM: Consider the distance x m from C where the SF changes its sign. Join all BM values as shown in Fig.2.59(c). Point of contraflexure: Point of contraflexure is the point where BM is zero. Consider the point which is distance from C Where BM is zero. Taking moment about that point, y = 6 is not a possible value. ⸫ The point of contraflexure is 1.2m from C. Result: (i) The SFD and BMD are shown in Fig.2.59(b) & (c) respectively. (ii) Maximum value of BM = 57.6 kN-m (iii) The point of contraflexure occurs at a distance of 1.2 m from end C. Example 2.47: Draw the SFD and BMD for the beam loaded as shown in Fig. 2.60. Given: As shown in Fig.2.60(a). To draw: SFD and BMD Solution: Taking moment about A, SF calculation: SF at C = 0 SF at B (without reaction RB) = 12 × 2 = 24 kN SF at B (with reaction RB) = 12 × 2 - RB = 24 - 64 = -40 kN SF at A= +RA = +32 kN Join all the SF values by inclined line as shown in Fig.2.60(b). BM calculation: BM at C = 0 BM at A = 0 Join the above BM values by parabolic curve as shown in Fig.2.60(c). Result: The SFD and BMD are shown in Fig.2.60(b) & (c). Example 2.48: Construct the SFD and BMD for the beam shown in Fig. 2.61(a). Given: As shown in Fig.2.61(a). To draw: SFD and BMD Solution: Taking moment about A, = 6 + 30 + 25 = 61 = 6 + 10 + 3.75 = 19.75 KN RA = 19.75 - RD = 19.75 - 12.2 RA = 7.55 kN SF calculation: SF at E = 0 SF at D (without reaction) SF at D (with reaction RD) = 3.75 - RD = 3.75 - 12.2 = - 8.45 kN SF at C = -8.45 + 10 = 1.55 kN SF at B = 1.55 kN SF at A = RA = 7.55 kN Connect the values between D and E by parabolic curve and all other values are joined as shown in Fig.2.61(b). BM calculation: BM at E = 0 BM at A = 0 Join the values between C and E by cubic curve and AB by parabolic curve as shown in Fig.2.61(c). Result: The SFD and BMD are drawn as shown in Fig.2.61(b) & (c) respectively. Example 2.49: Draw the SFD and BMD for the beam shown in Fig. 2.62(a). Given: As shown in Fig.2.62(a). To draw: SFD and BMD Solution: Taking moment about B, RB + RD = 1.5 × 2 + 2 × 2 + 6 = 13 kN RB = 13 - RD = 13 - 8.75 = 4.25 kN SF calculation: SF at E = 0 SF at D (without reaction RD) 2 × 2 = 4 kN SF at D (with reaction RD) = 4 - RD = 4 - 8.75 = -4.75 kN SF at C = -4.75 + 6 = 1.25 kN SF at B (without reaction RB) = -4.75 + 6 = 1.25 kN SF at B (with reaction RB) = 1.25 - RB = 1.25 - 4.25 = -3 kN SF at A = 0 Join all SF values as shown in Fig.2.62(b). BM calculation: BM at E = 0 BM at A = 0 Join all the BM values as shown in Fig.2.62(c). Result: The SFD and BMD are as shown in Fig.2.62(b) & (c) respectively.
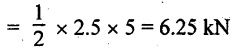
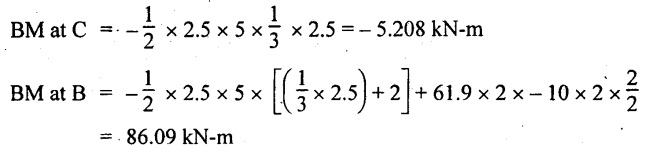


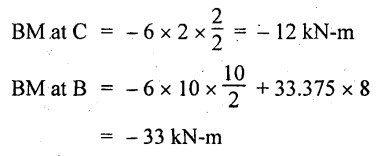


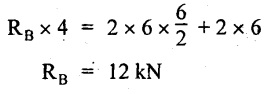
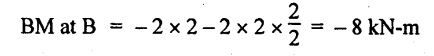


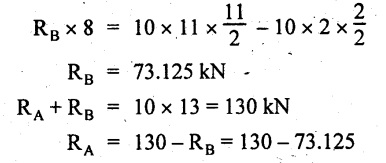
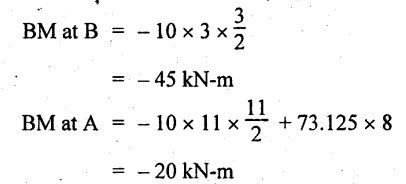


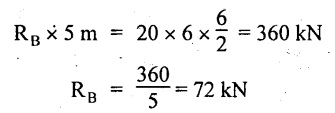
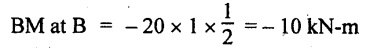
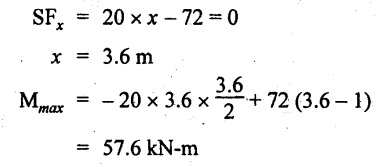
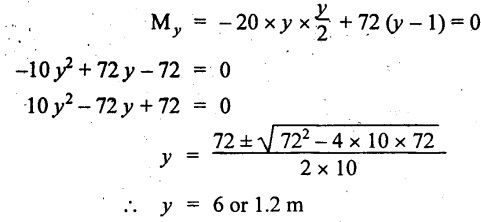
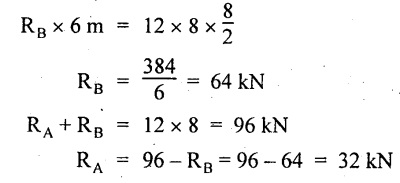
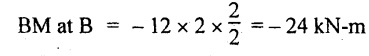

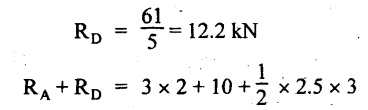

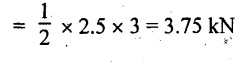
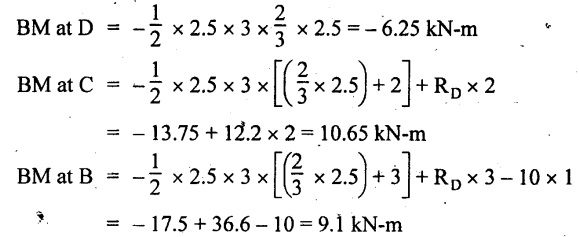
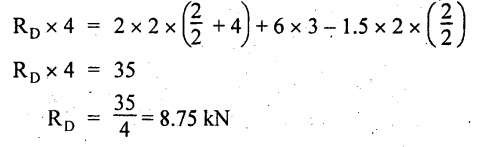
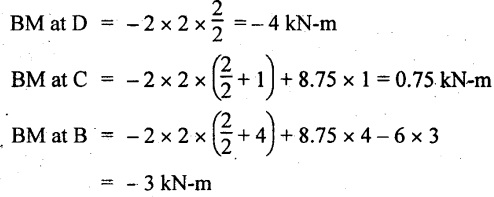
Strength of Materials: Unit II: Transverse Loading on Beams and Stresses in Beam : Tag: : Transverse Loading on Beams and Stresses in Beam - Strength of Materials - university solved problems on overhanging beam
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
