Strength of Materials: Unit III: Torsion
University solved problems
Torsion - Strength of Materials
University solved problems: Torsion - Strength of Materials
UNIVERSITY SOLVED PROBLEMS Example 3.19 A solid circular shaft is required to transmit 95 kW at 150 rpm. Find out the diameter of the shaft if permissible shear stress is 60 Mpa and angle of twist is 0.3°per meter length. Take C = 10 × 10 N/mm2. Given data: To find: Diameter of the shaft (D) Solution: We know that, Shear stress and angle of twist both are given. First case: Second case: Considering angle of twist (θ)
Suitable diameter for the shaft is 104.2 mm (i.e., greater of the two values). Result: Shaft diameter, D = 104.2 mm Example 3.20 Design a suitable diameter for a circular shaft required to transmit 120 kW at 180 rpm. The shear stress in the shaft not to exceed 70 N/mm2 and the maximum torque exceeds the mean by 40%. Calculate the angle of twist in a length of 2m. Take C = 0.8 × 105 N/mm2. Given data: To find: Angle of twist (θ)
Solution: We know that, Result: Angle of twist, θ = 2.3° Strength of Materials for Mechanical Engineers The external and internal diameters of hollow shaft are 40 cm and 20 cm. Find the maximum torque which the shaft can transmit, if the angle of twist is not to exceed 1° in a length of 10 meters. Take C = 0.8 × 106 N/mm2. Given data: To find: Maximum torque (T) Solution: Angle of twist (θ) is given. So,
Result: Maximum Torque, T = 3.41 × 109 N/mm2 A hollow shaft is to transmit 300 kW at 100 rpm. If the shear stress is not to exceed 60 N/mm2 and the internal diameters 0.6 times the external diameter. Find the internal and external diameters of the shaft. The maximum torque exceeds the mean by 10%. Given data: To find: External diameter (D) Internal diameter (d) Solution: We know that, Maximum torque for hollow shaft (considering shear stress) Result: External diameter, D = 145.30 mm Internal diameter, d = 87.18 mm A solid shaft is to transmit 300 kW at 100 rpm if the shear stress is not to exceed 80 N/mm2. Find the diameter of the shaft. If this shaft were to be replaced by hollow shaft of same material and length with an internal diameter of 0.6 times the external diameter, what percentage saving in weight is possible. Given data: To find: Solution: We know that, Torque for solid shaft (considering shear stress) Solid shaft is replaced by hollow shaft In hollow shaft, Inner diameter, d Outer diameter, D1 Torque transmitted by hollow shaft We know that, Torque transmitted by hollow shaft is equal to the torque transmitted by solid shaft when the solid shaft is replaced by hollow shaft. Equating (1) and (2), Result: Percentage of saving in weight = 29.8% Example 3.24 Find the diameter of a solid circular shaft to transmit 150 kW of power at 300 rpm. If the allowable shear stress is 90 Mpa and twist is 1° over 2 m length of the shaft. Take rigidity modulus as 90 Gpa. Given data: To find: Diameter of the shaft Solution: We know that, Shear stress and angle of twist both are given. First case: Second case: Considering angle of twist (θ)
From the above two cases, we find that suitable diameter for the shaft is 89.2 mm (i.e., greater of two values). Result: Shaft diameter, D = 89.2 mm Example 3.25 A solid circular shaft transmits 75 kW at 200 rpm. Find the shaft diameter if the twist in the shaft is not to exceed 1o in 2m length of the shaft and the shearing stress is limited to 50 N/mm2. Take G = 100 GN/m2.
Given data: To find: Diameter of the shaft Solution: We know that, Shear stress and angle of twist both are given. First case: Considering shear stress (τ)
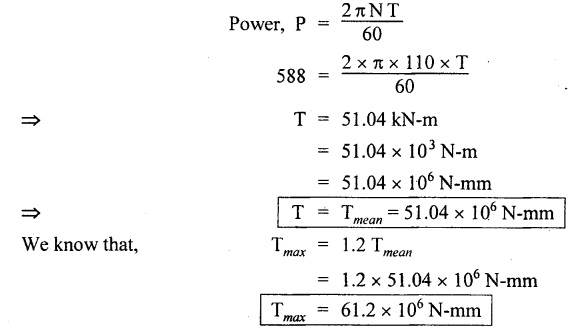
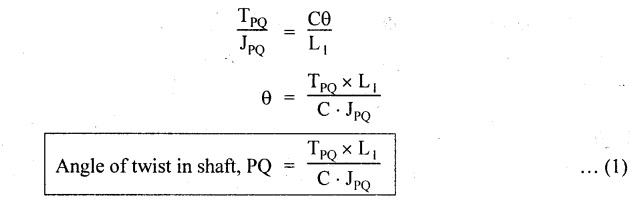
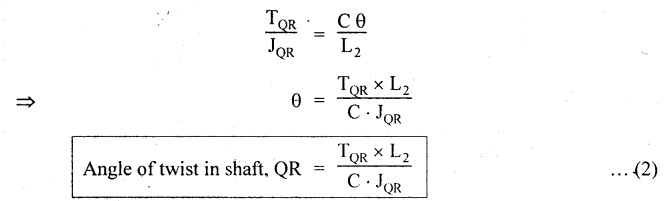
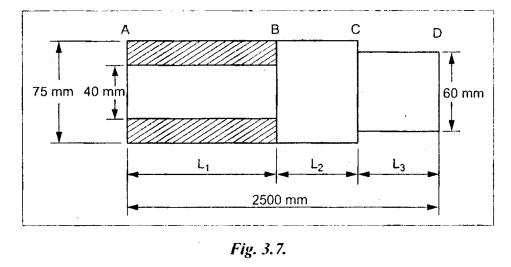
Second case: Considering angle of twist (θ) From the above two cases, we find that suitable diameter for the shaft is 80.9 mm (i.e., greater of two values). Result: Shaft diameter, D = 80.9 mm A solid circular shaft of 12 cm diameter is transmitting 150 kW at 150 rpm. Find the intensity of shear stress induced in the shaft. Given data: D = 12 cm = 120 mm P = 150 kW N = 150 rpm To find: Shear stress (τ) Solution: We know that, Result: Shear stress, τ = 28.14 N/mm2 A hollow shaft of diameter ratio 3/8 is required to transmit 588 kW at 110 rpm. The maximum torque exceeds the mean by 20%. The shear stress is limited to 63 N/mm2 and the twist should not be more than 0.0081 rad. Calculate the external diameter required satisfying both the conditions. Take G = 84 Gpa. Length = 3 m. Given data: To find: External Diameter (D) Solution: We know that, Shear stress and angle of twist both are given. First case: Considering shear stress (τ) Second case: Considering angle of twist (θ) From the above two cases, we find that external diameter of the shaft is 229.09 mm and internal diameter is 85.90 (i.e., greater of the two values). Result: External diameter, D = 229.09 mm Internal diameter, d = 85.90 mm A shaft is required to transmit power of 300 kW running at a speed of 120 rpm. If the shear strength of the shaft material is 70 N/mm2. Design a hollow shaft with inner diameter equal to 0.75 times the outer diameter. Given data: P = 300 kW N = 120 rpm τ = 70 N/mm2 d = 0.75 D To find: Inner Diameter (d) and outer diameter (D) Solution: We know that, Result: Internal diameter, d = 102.33 mm External diameter, D = 136.45 mm Example 3.29 A hollow circular shaft 20 mm thick transmits 300 kW at 200 rpm. Determine the inner diameter of the shaft if the shear strain is not to exceed 8.6 × 10-4. Take C = 80 GN/m2. Trial and error method can be used. Given data: To find: Inner Diameter (d) Solution: Outer radius R = r + 20 Shear stress is given. For hollow shaft Result: Inner diameter, d = 68 mm A solid shaft A of 50 mm diameter rotates at 250 rpm. Find the power that can be transmitted for a limiting shear stress of 60 N/mm2 in the steel. It is proposed to replace A by hollow shaft B of the same external diameter but with the limiting shear stress of 75 N/mm2. Determine the internal diameter of B to transmit the same power at the same speed. Given data: Solid shaft A: Diameter, D = 50 mm Speed, N = 250 rpm Shear stress, T = 60 N/mm2 To find: Power, P Hollow shaft B: To find: Internal diameter, (d) Solution: We know that, Substitute T value in equation (1) Solid shaft is replaced by hollow shaft. Torque transmitted by solid shaft is equal to the torque transmitted by hollow shaft. Torque transmitted by hollow shaft [Considering shear stress]. Result: Determine the diameter of a solid shaft transmitting 300 kW at 250 rpm. The maximum shear stress should not exceed 30 N/mm2 and the twist should not be more than 1° in a shaft length of 2m. Take G = 100 kN/mm2. Given data: To find: Diameter of the solid shaft, D Solution: We know that, Shear stress and angle of twist both are given. First case: Considering shear stress (τ) Second case: Considering angle of twist (θ) From the above two cases, we find that suitable diameter of the shaft is 124.8 mm (i.e., greater of two values). Result: Shaft diameter, D = 124.8 mm A solid circular shaft is subjected to a torque of 150 N-m. Find the minimum diameter required if the allowable shear stress is 100 N/mm2 and allowable twist is 1° per 3m length of shaft. C = 100 kN/mm2. Given data: To find: Diameter of the solid shaft, D Solution: Shear stress and angle of twist both are given. First case: Considering shear stress (τ) Second case: Considering angle of twist (θ) From the above two cases, we find that suitable diameter of the shaft is 40.52 mm (i.e., greater of two values). Result: Shaft diameter, D = 40.52 mm A solid circular shaft transmits 75 kW power at 200 rpm. Calculate the shaft diameter, if the twist in the shaft is not to exceed 1o in 2m length of the shaft, and shear stress is limited to 50 N/mm2. Take C = 1 × 105 N/mm2 Given data: To find: Diameter of the solid shaft, D Solution: We know that, Shear stress and angle of twist both are given. First case: Considering shear stress (τ) Second case: Considering angle of twist (θ) From the above two cases, we find that suitable diameter of the shaft is 80.93 mm (i.e., greater of two values). A solid shaft is subjected to a torque of 100 N-m. Find the necessary shaft diameter if the allowable shear stress is 100 N/mm2 and the allowable twist is 3° per 10 diameter length of the shaft. Take C = 1 × 105 N/mm2. Given data: T = 100 N-m = 100 × 103 N-mm τ = 100 N/mm2 To find: Diameter of the solid shaft, D Solution: Shear stress and angle of twist both are given. First case: Considering shear stress (τ) Second case: Considering angle of twist (θ) From the above two cases, we find that suitable diameter of the shaft is 17.20 mm (i.e., greater of two values). A hollow shaft, having an internal diameter 50% of its external diameter, transmits 600 kW at 150 rpm. Determine the external diameter of the shaft if the shear stress is not to exceed 65 N/mm2 and the twist in a length of 3m should not exceed 1.4 degrees. Assume maximum torque 1.2 times the mean torque and modulus of rigidity = 1 × 105 N/mm2. Given data: Internal diameter = 0.5 external diameter To find: External Diameter of the shaft (D) Solution: We know that, Shear stress and angle of twist both are given First case: Considering shear stress (τ) Second case: Considering angle of twist (θ) From the above two cases, we find the external diameter of the shaft is 156.42 mm (i.e., greater of two values). Result: External diameter, D = 156.42 mm When a shaft is made up of different lengths and of different diameters, it is termed as shaft of varying section. For such a shaft, the torque induced in its individual sections should be calculated first. The strength of the shaft is the minimum of all these torques. Example 3.36 A shaft PQR of 0.6 m length and 0.050 m external diameter is bored, for a part of its length PQ, to a 0.025 m diameter and for the remaining length QR to a 0.035 m diameter bore. If the shear stress is not to exceed 70 N/mm2, find the maximum power that the shaft can transmit at a speed of 150 rpm. If the angle of twist in the length of 0.025 m diameter bore is equal to that in the 0.035 m diameter bore, find the length of the shaft that has been bored to 0.025 m and 0.035 m diameter. Given data: To find: 1. Maximum power, P 2. Length of shaft, (PQ), L1 3. Length of shaft, (QR), L2 Solution: Torque transmitted by hollow shaft PQ is given by Torque transmitted by hollow shaft QR is given by From the above two cases, we find that torque transmitted by the whole shaft is 1.30 × 106 N-mm i.e., minimum of the two values. Torque transmitted by hollow shaft PQ (considering angle of twist) is given by Torque transmitted by hollow shaft QR (considering angle of twist) is given by Equating (1) and (2) We know that, torque (T) and shear modulus (C) are same for the given shaft We know that, L = L1 + L2 Result: 1. Maximum power, P = 20.41 kW 2. Length of the shaft (PQ), L1 = 330.94 mm 3. Length of the shaft (QR), L2 = 296.06 mm A steel shaft ABCD having a total length of 2500 mm having different diameters as shown in Fig. If the angle of twist is the same for each section, determine the length of each section and the total angle of twist if the maximum shear stress in the hollow portion is 60 N/mm2 and modulus of rigidity, C is 1 × 105 N/mm2. Given data: To find: 1. Length of each section i.e., L1, L2, L3 2. Total angle of twist, θ Solution: We know that, Torque transmitted by hollow shaft AB (considering angle of twist) Torque, T and shear modulus, C are same for each portion. From equation (4), we know that, Substitute L2 value in equation (5) Substitute L2 value in equation (6) Torque transmitted by hollow shaft AB is given by Torque transmitted by hollow shaft AB (considering angle of twist) is given by, Result:
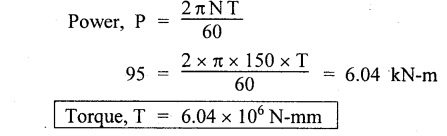


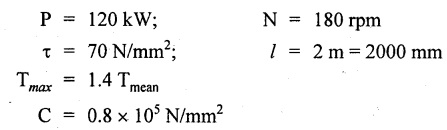

Example 3.21
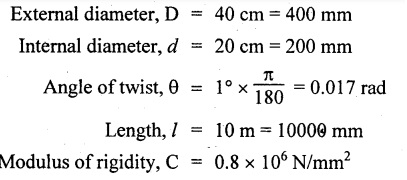

Example 3.22
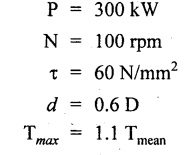


Example 3.23



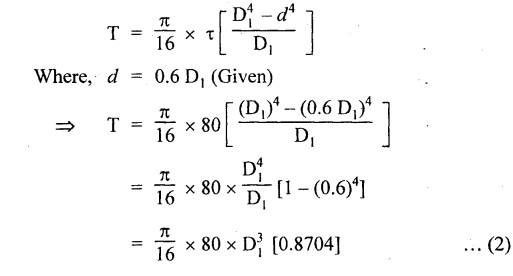


ANNA UNIVERSITY SOLVED PROBLEMS
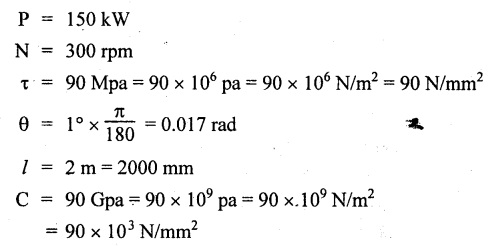

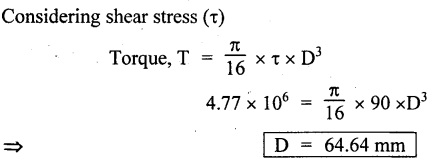





Example 3.26
 Result:
Result:Example 3.27



Example 3.28





Example 3.30
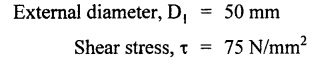

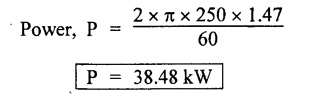

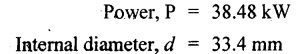
Example 3.31


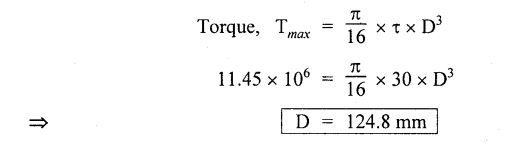

Example 3.32
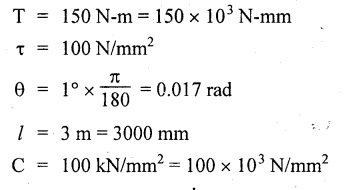


Example 3.33




Example 3.34
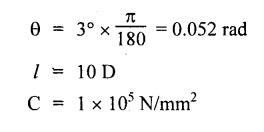


Example 3.35




14. SHAFT OF VARYING SECTION OR STEPPED SHAFT
15. SOLVED PROBLEMS

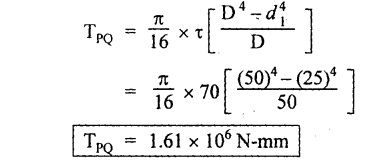
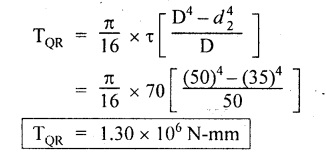

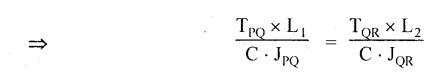


Example 3.37




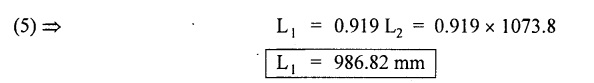
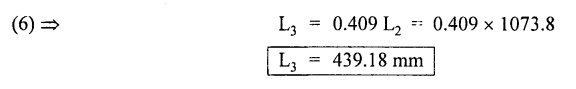
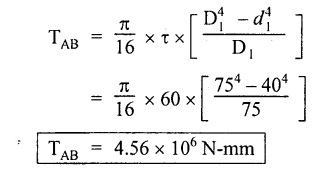


Strength of Materials: Unit III: Torsion : Tag: : Torsion - Strength of Materials - University solved problems
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
