Strength of Materials: Unit I: Stress, Strain and Deformation of Solids
University solved problems
Stress, Strain and Deformation of Solids - Strength of Materials
Stress, Strain and Deformation of Solids - Strength of Materials: University solved problems
UNIVERSITY SOLVED PROBLEMS Example 1.44: Determine the change in length, breadth and thickness of a steel bar 4 m lồng, 30 mm wide and 20 mm thick, when subjected to an axial pull of 120 kN in the direction of its length. Take E = 200 GPa and Poisson's ratio = 0.3. Given: Length, L = 4 m = 4000 mm; Wide, b = 30 mm Thickness, t = 20 mm; Axial pull, P = 120 kN = 120 × 103 N Young's Modulus, E = 200 GPa = 200 × 109 Pa = 200 × 109 N/m2 = 200 × 103 N/mm2; Poisson's ratio, 1/m = 0.3 To find: 1. Change in length, δL, 2. Change in breadth, δb, 3. Change in thickness, δt. Solution: We know that, Result: Change in length, δL = 4 mm Change in breadth, δb = 9 × 10-3 mm Change in thickness, δt = 6 × 10-3 mm Example 1.45: A bar of 30 mm diameter is subjected to a Pull of 60 kN. The measured extension on gauge length of 200 mm is 0.09 mm and the change in diameter is 0.0039. Calculate the Poisson's ratio and the value of the three moduli. Given: Diameter, d = 30 mm; Pull, P = 60 kN = 60 × 103 N Length, L = 200 mm; Change in length, δL = 0.09 mm Change in diameter, δd = 0.0039 mm To find: 1. Poisson's ratio, 1/m, 2. Young's Modulus, E, 3. Bulk Modulus, K, 4. Modulus of Rigidity, G. Solution: We know that, Substituting et, el values in equation (1), We know that, We know that, Result: 1. Poisson's ratio, 1/m = 0.28 2. Young's Modulus, E = 1.8 × 105 N/mm2 3. Modulus of Rigidity, G = 7.0 × 104 N/mm2 4. Bulk Modulus, K = 1.36 × 105 N/mm2 Example 1.46: Find the young's modulus and Poisson's ratio of a metallic bar of length 300 mm, breadth 40 mm, depth 40 mm when the bar is subjected to an axial load of 40 kN. Decrease in length is 0.75 mm and the increase in breadth is 0.03 mm. Also find the modulus of rigidity of the bar. Given: Length, L = 300 mm Breadth, b = 40 mm Depth, t = 40 mm Axial load, P = 40 kN = 40,000 N Decrease in length, δL = 0.75 mm Increase in breadth, δb = 0.03 mm To find: 1. Young's Modulus, E, 2. Poisson's ratio, 1/m, 3. Modulus of Rigidity, G. Solution: We know that, Substituting et, el, values in equation (1), We know that, Result: 1. Young's Modulus, E = 1 × 104 N/mm2 2. Poisson's ratio, 1/m = 0.3 3. Modulus of Rigidity, G = 3846.15 N/mm2 Example 1.47: When a metallic bar of length 25 cm, breadth 3 cm and depth 2 cm is subjected to an axial load of 240 kN. The decrease in length is 0.05 cm and increase in breadth is 0.002 cm. Determine the bulk modulus of the material. Given: Length, L = 25 cm = 250 mm Breadth, b = 3 cm = 30 mm Depth, t = 2 cm = 20 mm Axial load, P = 240 kN = 240 × 103 N Change in length, δL = 0.05 cm = 0.5 mm Change in breadth, δb = 0.002 cm = 0.02 mm To find: (1) Bulk Modulus, K. Solution: We know that, Result: 1. Bulk modulus, K = 1.96 × 105 N/mm2 Example 1.48: For a given material, Young's Modulus is 1 × 105 N/mm2 and Modulus of rigidity is 4 × 10 N/mm2. Find the bulk modulus and lateral contraction of a round bar of 50 mm diameter and 2.5 m long, when length is increased 2.5 mm. Given: Young's Modulus, E = 1 × 105 N/mm2 Modulus Rigidity, G = 4 × 104 N/mm2 Diameter, d = 50 mm Length, L = = 2.5 mm = 2500 mm Change in length, δL = 2.5 mm To find: 1. Bulk Modulus, K, and 2. Lateral contraction of round bar, δd. Solution: We know that, We know that, Substituting (1/m) and el values in equation (2), We know that, Substituting (1/m) values in equation (1), Result: 1. Bulk Modulus, K = = 6.6 × 104 N/mm2 2. Change in diameter, δd = 0.0125 mm Example 1.49: A bar of cross section 8 mm × 8 mm is subjected to an axial pull of 8000 N. The lateral dimension of the bar is found to be 7.996 × 7.996. If the modulus of rigidity of the material is 9.6 × 10 N/mm2. Determine the Poisson's ratio and modulus of elasticity. Given: Area, A = 8 mm × 8 mm = 64 mm Axial pull, P = 8000 N Lateral dimensions = 7.996 × 7.996 mm Modulus of Rigidity, G = 9.6 × 104 N/mm2 To find: (1) Poisson's ratio, 1/m, (2) Modulus of Elasticity, E. Solution: We know that, Substituting el and et values in equation (1), Result: Poisson's ratio, 1/m = 3.3 Young's Modulus, E = 8.3 × 105 N/mm2 Example 1.50: Calculate the modulus of rigidity and bulk modulus of a cylindrical bar of diameter 25 mm and length 1.6 m. If the longitudinal strain in a bar during tensile stress is four times the lateral strain. Determine the change in volume, when the bar is subjected to a hydrostatic pressure of 100 N/mm2. Take E = 1 × 105 N/mm2. Given: Diameter, d = 25 mm Length, L = 1.6 m = 1600 mm Longitudinal strain = 4 × Lateral strain el = 4et Stress, σ = 100 N/mm2 Young's modulus, E = 1 × 105 N/mm2 To find: 1. Modulus of Rigidity, G, 2. Bulk Modulus, K, 3. Change in volume, dV. Solution: We know that, We know that, Result: 1. Modulus of Rigidity, G = 4 × 104 N/mm2 2. Bulk modulus, K = 0.66 × 105 N/mm2



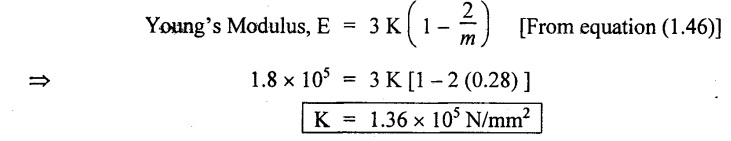


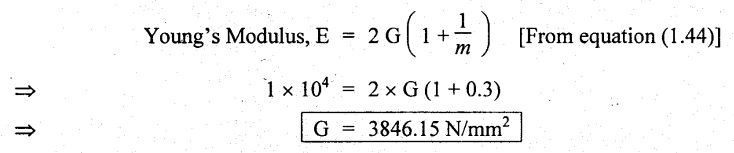




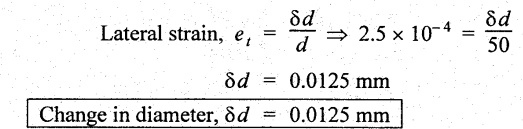
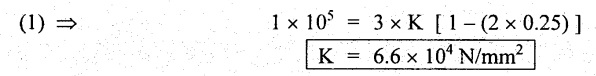




Strength of Materials: Unit I: Stress, Strain and Deformation of Solids : Tag: : Stress, Strain and Deformation of Solids - Strength of Materials - University solved problems
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
