Strength of Materials: Unit III: Torsion
types of springs
Torsion - Strength of Materials
We may divide the springs mainly into two categories: 1. Torsion spring 2. Bending spring
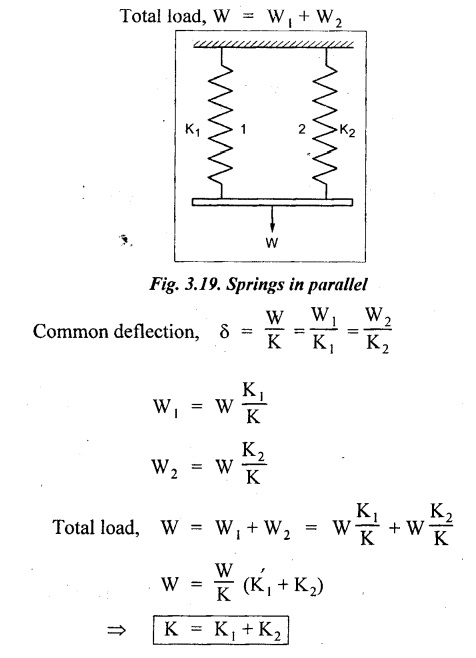
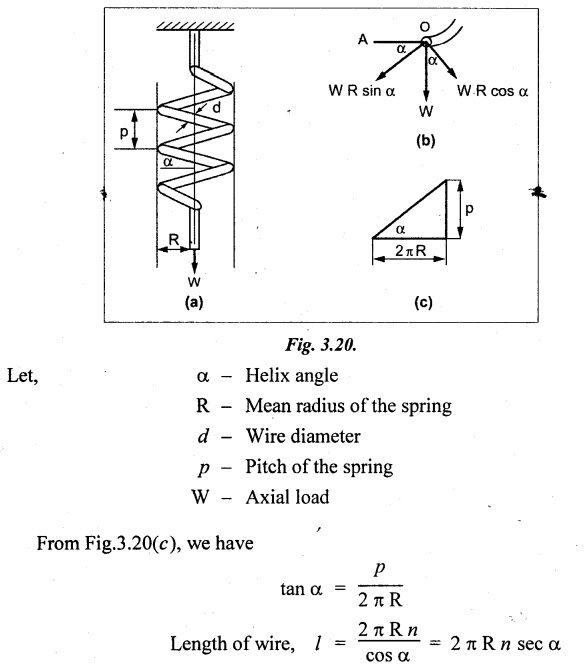
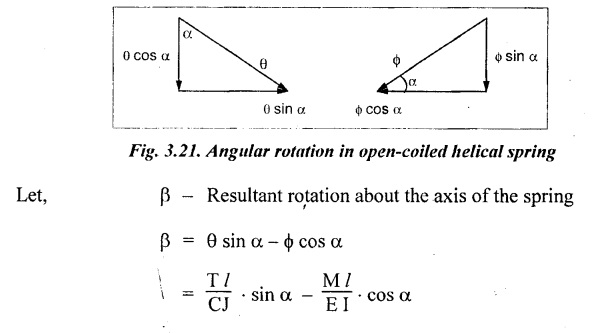
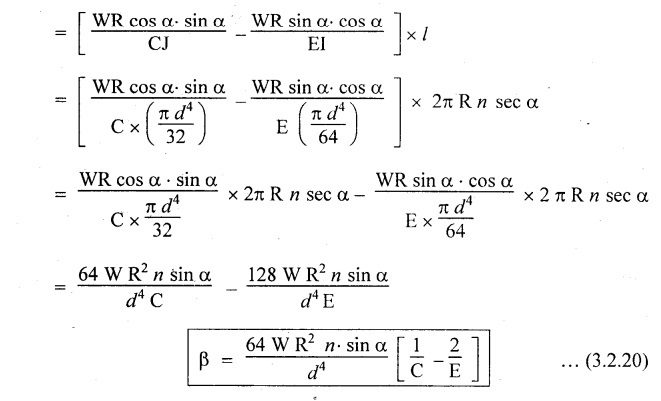
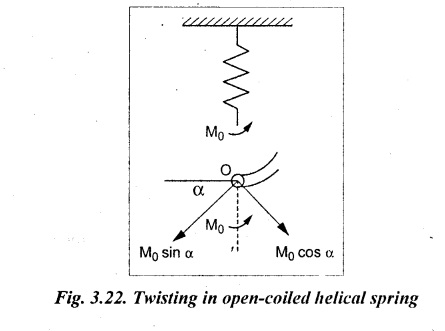
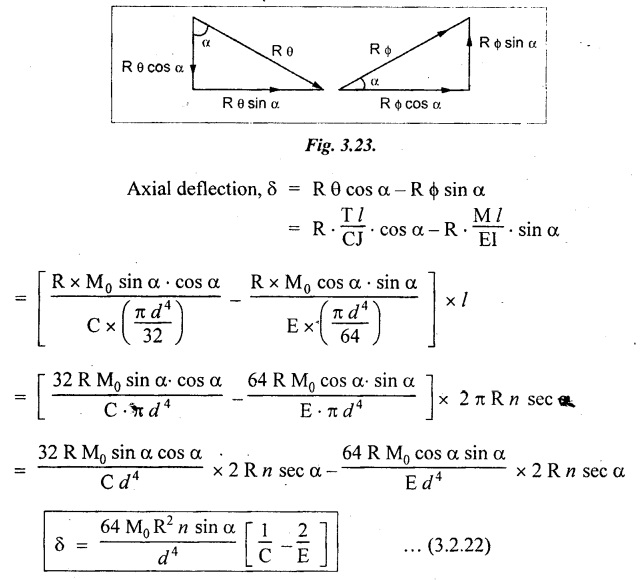
SPRINGS A spring is a device which is used to absorb energy by taking very large change in its form without permanent deformation and then release the same when it is required. For example, a spring in the clock work is used to absorb energy when the clock wound. This absorbed energy is gradually released at a show but continuous rate as the clock runs. Another common example is the carriage springs or leaf spring in an automobile which absorb road shock by continuously absorbing energy due to shock by their deformation and then dissipating the same by vibrating. We may divide the springs mainly into two categories: 1. Torsion spring 2. Bending spring A torsion spring is the one which is subjected to a twisting moment and the resilience is mainly due to torsion. The helical springs subjected to axial pull fall under this category. The helical springs which are formed by winding a wire around a cylindrical mandrill in the form of helix. A bending spring is the one which is subjected to bending only and resilience is mainly due to bending. The leaf or plate springs fall under this category. The stiffness of a spring is defined as the load required to produce unit deflection. It is one type of torsion spring. In this type of spring, the wire is turned so closely that each turn is nearly right angle to the axis of the spring and the gap between two consecutive turns is small. In closed coiled helical springs, an axial pull or thrust produces only torsion on the material of the spring. The types of stresses that are produced in a spring loaded at the end in a general way would be. (i) Direct shear stress (ii) Torsional shear stress (iii) Bending stress In a closed coiled spring, direct shear stress and the bending stresses are negligible when it is subjected to axial pull W, where as the direct shear stress and the torsional shear stresses are neglected when it is subjected to a couple at the end. Consider a closed coil spring of mean coil radius 'R' and the wire diameter d, number of complete coils 'n' and 'l' the total length of wire in it, as shown in Fig.3.17. Let 'δ' be the axial deflection of the spring at the free end under load 'W' and 'ϕ' be the angle of rotation of the free end under axial couple M. If 'n' be the number of coils in the spring, the total length of the wire 'l' will be, l = 2 π R n or π Dn Consider a close coiled helical spring subjected to axial load 'W' at one end. The twisting moment exerted on the wire Angle of twist for whole length of the spring, Thus, the free end will twist through an angle θ. Consequently, the free end will have an axial movement Rθ. If 8 is the axial movement or deflection, The stiffness, K of the spring is the load required to produce unit deflection, The maximum shear stress induced in any section under axial load is obtained by torsion equation. The amount of strain energy stored in the spring, When a closely coiled spring is held at one end and subjected to twisting couple M about the axis of the spring, the coil will bend in or out depending upon the sense of the couple.. The wire of the spring will resist a bending moment M at every cross section. Equating the work done by axial couple to the strain energy, From bending equation, Let the weight 'P' falls on a spring from a height 'h' measured from the uncompressed state of the spring. Let 'W' is the equivalent uniformly applied load and 'δ' is the deflection of the spring under load 'W'. Work done by falling weight = P (h + δ) Work saved in the spring = 1/2 W δ Equating above two works From the above equation we can find out the required values. In many situations, the combination of two or more springs either may be connected in series or parallel are required. (i) Springs in series Two springs of stiffness K1 and K2 are connected in series and loaded with W as shown in Fig.3.18. In this case, each spring is subjected to the same load applied at the end of one spring. Therefore the total deflection of the assembly is equal to the algebraic sum of the deflection of the two springs. (ii) Springs in parallel: Two springs of stiffness K1 and K2 are connected in parallel, loaded with W, as shown in Fig.3.19. Let, load shared by the two springs be W1 and W2 . Therefore, the deflection of each spring is same. In open coiled helical spring, there is large gap between two consecutive turns. Here the helix angle a plays an important role. As a result of large gap between consecutive coils, these springs can take compressive as well as tensile loads. Helix angle ( α ) is the angle which the coils make with planes perpendicular to the axis of the spring. Consider an open-coiled helical spring as shown in Fig.3.20(a) is subjected to axial load W. (i) Axial deflection: The load W will cause a moment WR about the horizontal axis OA. This moment can be resolved into two components along OX and OY. Along OX, torque, T = WR cos α Along OY, bending moment, M = WR sin α The combined strain energy stored in the spring under bending and torsion is, The average external work done on the spring under load, Substituting (3.2.16), (3.2.17), (3.2.18) values in equation (3.2.15) (ii) Angular rotation On account of M there is bending in the plane of axis of the wire and due to T there is a twisting in the wire as shown in Fig.3.21. The horizontal components produce rotation about the axis of the spring. Consider an open-coiled helical spring under the action of axial twisting couple M0 about the axis of the spring as shown in Fig.3.22.
(i) Axial rotation The axial twisting couple can be divided into two components. For equilibrium condition, External work done = Strain energy stored in the spring (ii) Axial deflection The twisting couple M produces axial deflection along with rotation. (i) Axial load: Similarly, (ii) Axial torque: Similarly, Spring index is defined as the ratio of the mean diameter of the spring to the diameter of the spring wire. Closed coil helical spring: 3. Strain energy stored (subjected to axial load) 4. Strain energy stored (subjected to axial twisting couple) Open coil helical spring: 4. Axial deflection (spring subjected to axial load) 5. Angle of rotation [spring subjected to axial load] 6. Angle of rotation (spring subjected to axial twisting couple) 7. Axial deflection, (spring subjected to axial twisting couple) Example 3.51 A closed coil helical spring of 8 mm diameter wire with 12 coils of mean diameter 100 mm carries an axial load of 400 N. Find the shear stress induced and deflection caused. What is the strain energy stored? Take C = 8 × 106 N/cm2. Given data: To find: (i) τ (ii) δ (iii) U Solution: We know that shear stress in closed coil helical spring Result: Shear stress on the spring, τ = 198.944 N/mm2 Deflection of the spring, δ = 117.18 mm Strain energy stored, U = 23.43 × 103 N/mm2 A closed coil helical spring made out of 8 mm diameter wire has 18 coils. Each coil is of 80 mm mean diameter. If the maximum allowable stress in the spring is 140 Mpa, determine the allowable load on the spring, elongation of the spring and stiffness of the spring. Take C = 82 kN/mm2. Given data: To find: (i) W (ii) δ (iii) K Solution: We know that shear stress of the closed coil helical spring Result: Allowable load on the spring, W = 351.86 N Deflection of the spring, δ = 77.24 mm Stiffness of the spring, K = 4.55 N/mm A closed coil helical spring is made of steel rod having diameter 10 mm. The mean coil diameter of the spring is 120 mm and the number of complete turns is 12. The modulus of rigidity of the material of the spring is 0.86 × 105 Mpa. If this spring is subjected to an axial load of 200N. Calculate, (i) Axial deflection (ii) Maximum shear stress Given data: To find: (1) δ, (ii) τ Solution: We know that, Result: (i) Axial deflection of the spring, δ = 38.57 mm (ii) Maximum shear stress, τ = 61.12 N/mm2 A closed coil helical spring is to deflect 1 mm under the axial load of 100N at shearing of 90 N/mm2. The spring is to be made of round wire having rigidity modulus of 80 × 104 N/mm2. The mean diameter of the spring is to be 10 times the diameter of the wire. Find the diameter and length of the wire necessary to form the spring? Given data: To find: (i) d, (ii) l Solution: Maximum shear stress of the spring, We know that deflection of the spring Result: Wire diameter of the spring, d = 5.38 mm Length of the wire required, l = 1002.8 mm A wagon weighing 18 kN is moving at 5Km/hr. How many springs each of 20 coils will be required in a buffer stop to absorb the energy of motion during a compression of 175 mm. The mean diameter of coils is 250 mm and the diameter of steel rod comprising the coil is 22 mm. Take C = 82 Gpa. Given data: To find: Number of springs Solution: Kinetic energy absorbed by buffer springs, Result: Number of springs required = 15 A safety valve which is placed on a pressure vessel has 120mm diameter is used to blow off at a pressure of 1.23 N/mm2 gauge. It is held by a close coiled compression spring of circular steel bar. The mean diameter is 180mm and initial compression is 20 mm. Find the diameter of steel bar and the number of turns necessary if the shear stress allowed is 90 N/mm2. Take C = 0.82 × 105 N/mm2. Given data: To find: (i) Diameter of steel bar (d) (ii) Number of turn required (n) Solution: Total force on the valve, W = Area of valve × Pressure Result: Diameter of spring wire, d = 41.378 mm Number of turns required, n = 8 Two concentric close coiled springs are employed to control a valve, which requires a force of 155N to open the same by 12mm. The outer spring has 14 coils of 16mm mean radius and 4mm wire diameter. It is compressed by 6 mm initially when the valve is closed. The free length of the inner spring is 8mm more than that of the outer one. Determine the stiffness of the inner spring and also the number of turns it has if its mean diameter of 20mm and wire diameter of 2.5 mm. Take C = 80 Gpa. Given data: To find: Solution: The total force for concentric spring is 155 N. The force shared by outer spring is 100.44 N. Therefore remaining 155 - 100.44 N is shared by inner spring for deflection of 18 + 8 m = 26 mm. Force required to compress the inner spring for 26mm is, = 155 - 100.44 = 54.56 N Result: A composite spring has two closed coil helical springs connected in series. In both the springs, mean coil radius is 3.5 times the wire diameter. One spring is made out of 4mm wire diameter and has 16 turns where as other spring has 12 turns. Determine the wire diameter of the second spring if the stiffness of the composite spring is 1.3 N/mm. Assume C = 0.82 × 105 N/mm2 Given data: To find: Wire diameter of 2nd spring, (d2)
Solution: The same axial force (W) is applied on each spring when it is connected in series. δ1 and δ2 are the extensions in two springs. Result: Wire diameter of the 2nd spring, d2 = 0.6312 mm A truck weighing 150 kN is moving at a speed of 1.4m/s. Find the volume of the buffer spring which should be able to absorb the energy of the truck with the bending and shearing stresses not exceeding 275 Mpa and 215 Mpa respectively, if the impact is absorbed by (i) Compression of the spring (ii) Twisting of the spring. Assume the spring to be close coiled. E = 210 Gpa and C = 84 Gpa. Given data: To find: Volume of spring in case of (i) Compression of the spring (ii) Twisting of the spring Solution: Case (i): During compression of the spring, strain energy stored in the spring. Case (ii): During twisting of spring, strain energy Result: Volume of the spring, in case of (i) Compression of the spring = 108.88 × 106 mm3 (ii) Twisting of the spring = 332.78 × 106 mm3 A weight of 160N is dropped on to a close coiled helical spring made of 13mm steel wire and mean radius of 60mm with 22 coils. If the instantaneous compression is 90 mm, calculate the height of drop. Take C = 0.88 × 105 N/mm2. Given data: To find: Height of spring Solution: Let W be the equivalent gradually applied load to produce the same deflection (90 mm) as the given load. Result: Height of drop, h = 119.18 mm. An open-coiled helical spring is made out of 12mm diameter steel rod, the coils having 10 complete turns and a mean diameter 70mm, the angle of helix being 20°. The load W will cause the spring to elongate 22 mm. What is the value of W and the bending and shearing stress due to this load? If the 60Mpa bending stress is acting on the spring calculate the twisting couple to cause the same. Take E = 2.1 × 105 N/mm2 and C = 82 × 103 N/mm2 Given data: To find: Solution: In open-coiled helical spring, Result: An open coil helical spring is made of 10mm diameter wire and of mean diameter 90 mm had 15 coils, angle of helix being 15° Calculate the deflection under an axial load of 425N and maximum intensities of direct and shear stresses induced in the section of the wire. If the axial load of 425 N is replaced by an axial torque of 10 N-m, calculate the angle of rotation about the axis of the coil and the axial deflection. Take E = 2 × 105 N/mm2 and C = 0.84 × 105 N/mm2. Given data: To find: (1) For axial load (i) Deflection (ii) Direct stresses (iii) Maximum shear stress (2) For axial torque (i) Deflection (ii) Angle of rotation Solution: In open-coiled helical spring, Direct stress i.e., principle stresses If the axial load is replaced by axial torque 10 N-m. Result: In an open coil helical spring consists of 12 coils, the stresses due to bending and twisting are 73 Mpa and 92 Mpa respectively. When the spring is axially loaded, find the maximum permissible load and the diameter of wire for a maximum extension of 25 mm. Assume spring index as 9. E = 210. Gpa and C = 80 Gpa. Given data: To find: W and d Solution: Axial deflection Result: Diameter of spring wire, d = 6.35 mm Axial load, W = 174.19 NTYPES OF SPRINGS
STIFFNESS (K)
CLOSED COILED HELICAL SPRINGS
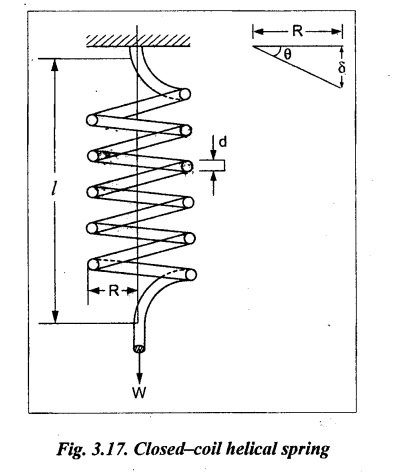
CLOSED - COIL HELICAL SPRING SUBJECTED TO AXIAL LOAD
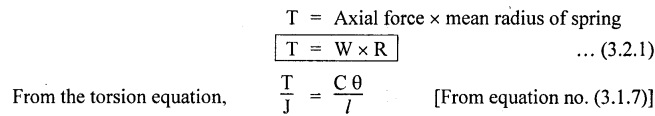

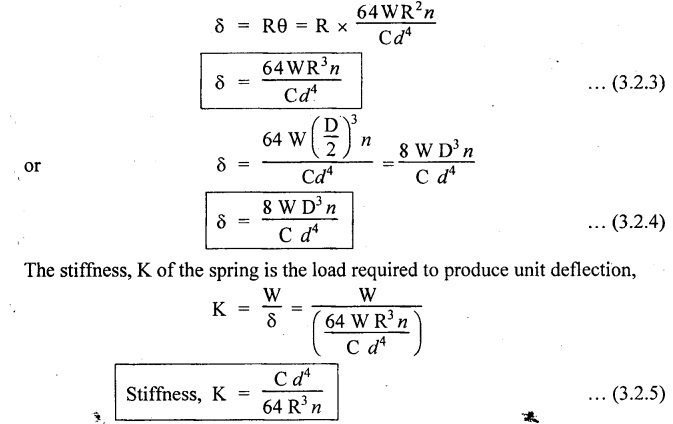
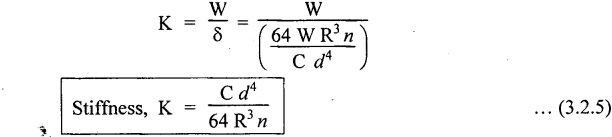
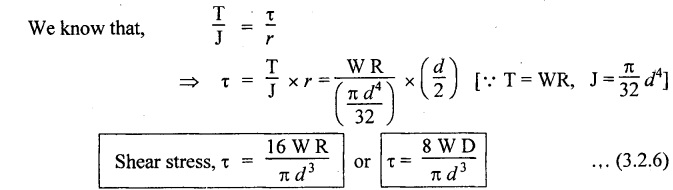
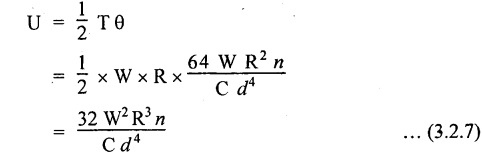

CLOSED-COIL HELICAL SPRING SUBJECTED TO AXIAL TWISTING COUPLE
 U
U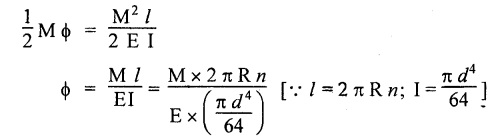
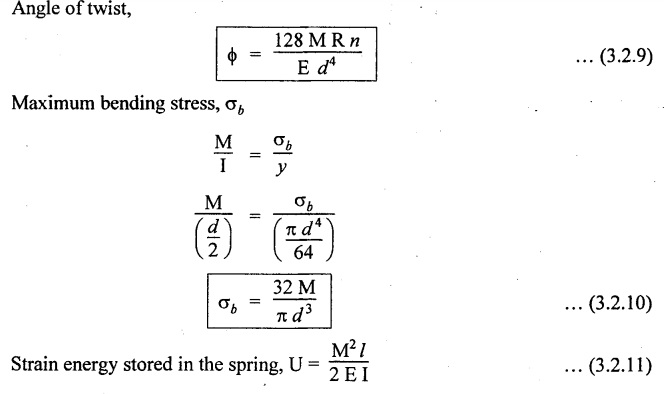

SPRINGS UNDER IMPACT LOAD

SPRINGS IN SERIES AND PARALLEL

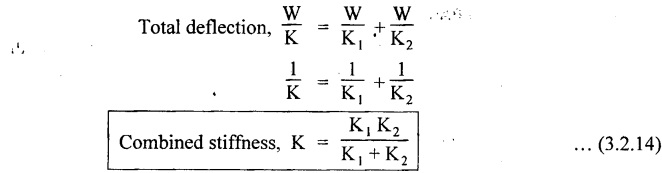
OPEN-COILED HELICAL SPRING
OPEN - COILED HELICAL SPRING SUBJECTED TO AXIAL LOAD
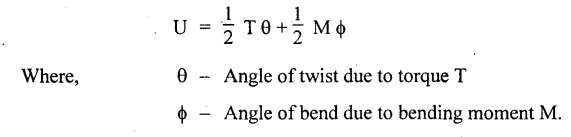


OPEN-COILED HELICAL SPRING SUBJECTED TO AXIAL TWISTING COUPLE


STRESSES IN THE SPRING WIRE



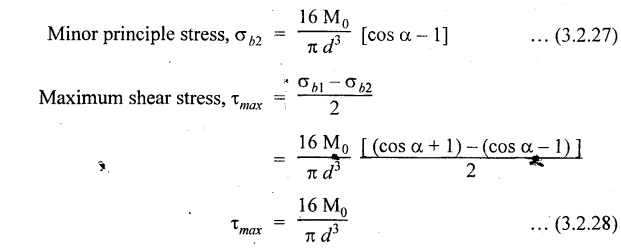
SPRING INDEX (S)

FORMULAE USED


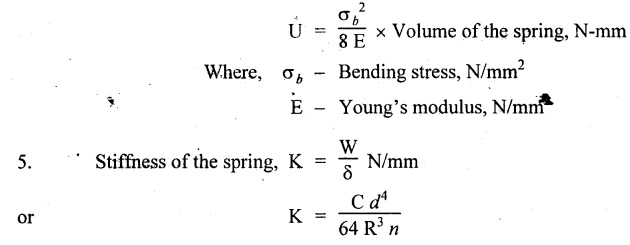


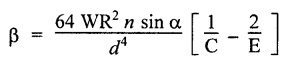
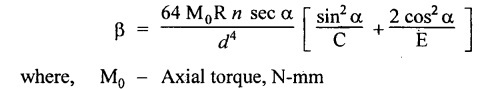
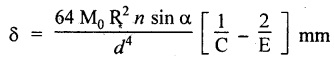
SOLVED PROBLEMS


Example 3.52

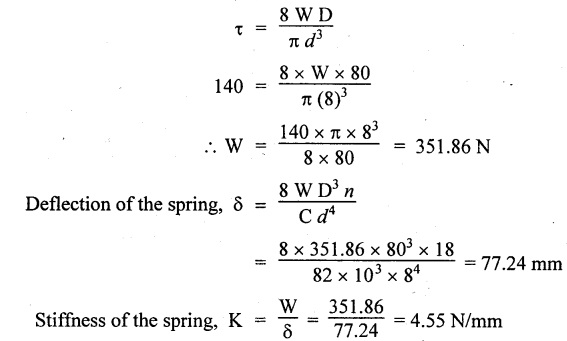
Example 3.53

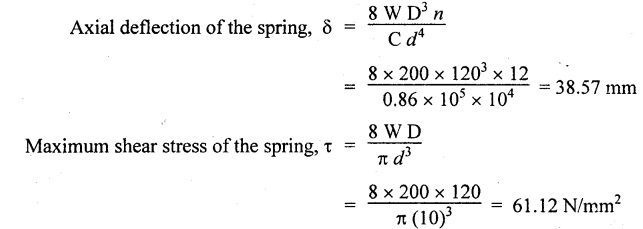
Example 3.54
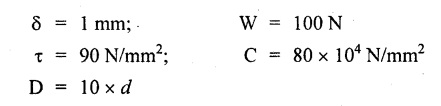
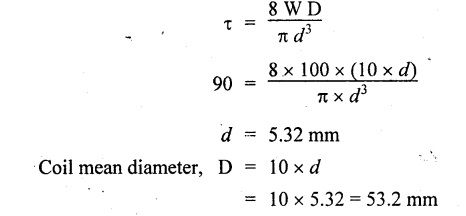
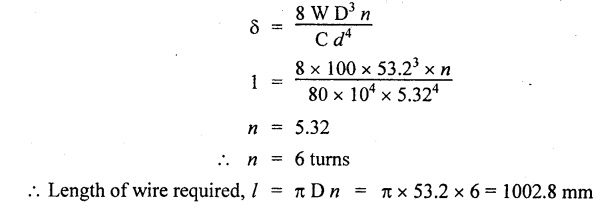
Example 3.55

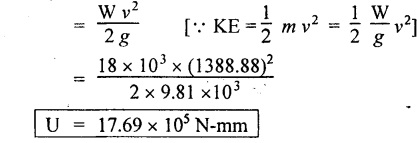

Example 3.56


Example 3.57



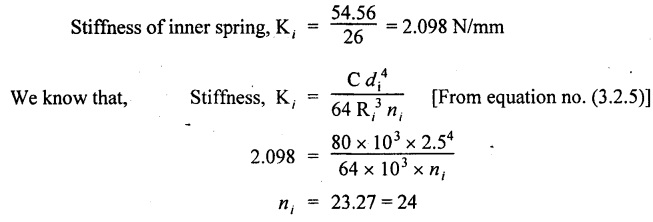
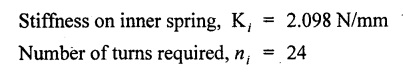
Example 3.58


Example 3.59

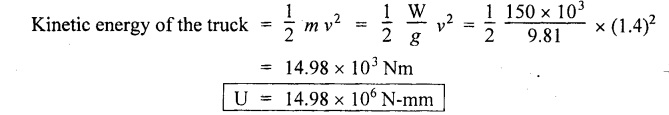
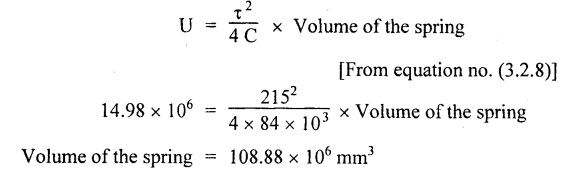
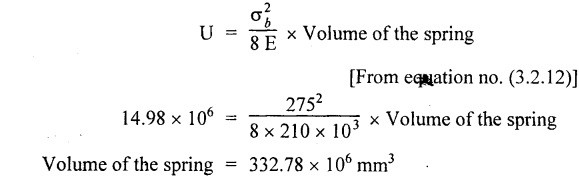 8
8Example 3.60


Example 3.61
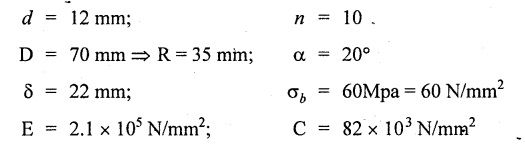
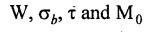


Example 3.62
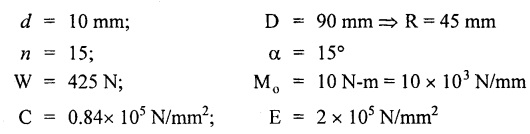
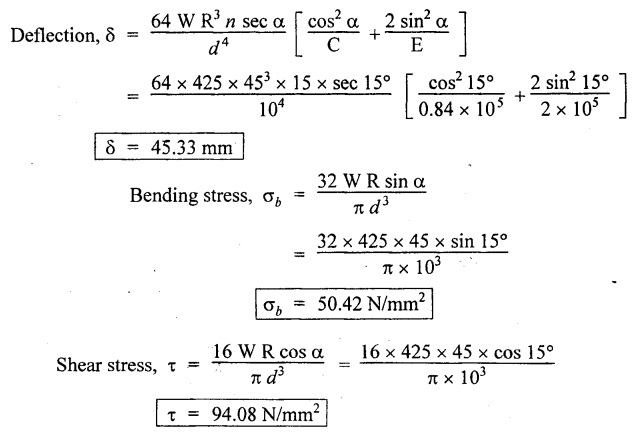
 б
б

Example 3.63


Strength of Materials: Unit III: Torsion : Tag: : Torsion - Strength of Materials - types of springs
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
