Strength of Materials: Unit IV: Deflection of Beams
Two mark Questions and Answers
Deflection of Beams - Strength of Materials
Two mark Questions and Answers: Deflection of Beams - Strength of Materials
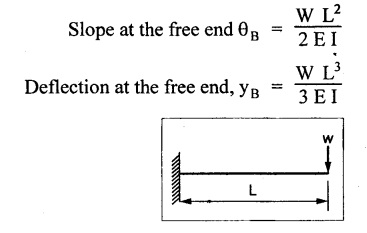
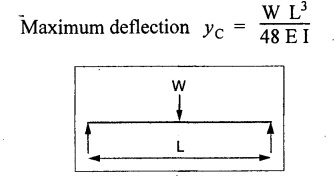
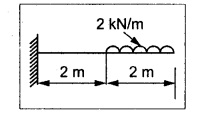
TWO MARK QUESTIONS AND ANSWERS 1. Where the slope and deflection will be maximum for the cantilever with point load at its free end? Both slope and deflection will be maximum at the free end. 2. What are the units of slope and deflection? Slope in radians Deflection in meter or millimeter. 3. State whether the following statement is true/false. In a cantilever beam, the maximum deflection equals sum of deflections by the individual load at the free end. Ans. True 4. Name the method which employs BMD for the calculation of slope and deflection. Moment area method. 5. Calculate area of BMD of a cantilever carrying UDL of W/m for the full span of 'L'. 6. What is the slope at the support for a SSB of constant EI and span L carrying central concentrated load? 7. Write the value of slope at the free end and of a cantilever beam of constant EI and span L carrying a concentrated load W at the free end? 8. State the two theorems in the moment area method. Mohr's theorem 1: The change of slope between any two points is equal to the net area of the BM diagram between these points divided by E I. Mohr's theorem 2: The total deflection between any two points is equal to the moment of the area of the BM diagram between these two points about the last point divided by EI. 9. Write the maximum value of deflection for a simply supported beam of constant EI, span L carrying central concentrated load W. 10. Where the maximum deflection will occur in a SSB loaded with UDL of w kN/m run? And note about the slope at that point. The maximum deflection will occurs at the center of the beam at which the slope is zero. 1. A load 'W' is placed at a distance 'x' from the fixed end of a cantilever of Wx2 (31-x) span L. Show that the deflection at the free end is y 2. A SSB of span L meters is loaded as shown in Fig. Find the equation for the deflection curve by Macaulay's method. 3. Derive an expression for slope and deflection of a cantilever beam carrying a UDL of w kN/m run. And also it carries a point load of W KN at its free end. 4. Obtain an expression for slope and deflection by moment area method of 'L' span SSB carrying central assumed point load. 5. Obtain an empirical relationship for slope and deflection of a 'L' span SSB carrying UDL of W kN/m run. 6. Obtain an expression for slope and deflection for the following figures. 1. A cantilever steel beam has a free length of 3 m. The moment of inertia of the section is 30 × 106 mm4. A concentrated load of 50 KN at the free end. Find the deflection at the free end using 1. Double integration method 2. Macaulay's method 3. Moment area method and 4. Conjugate beam method. Take E = 2 × 105 N/mm2. 2. A cantilever beam of 8 m long carries a UDL of 5 kN/m run and a load of W at the free end. If the deflection at the free end is 30 mm, calculate the magnitude of the load W, and the slope at the free end. E = 200 kN/mm2, I = 5 × 107 mm4. 3. A cantilever of 6m long carries a UDL of 50 kN/m throughout its length and a central concentrated load of 80 kN. Determine the slope and deflection at the free end by using moment area method. E = 2 × 105 N/mm2, I = 2 × 109 mm4. 4. A cantilever of 2 m long is of rectangular section of width 50 mm and depth of 75 mm. Calculate the maximum UDL that can be allowed on the entire length of the cantilever without exceeding a deflection of 4.5 mm at the free end and a bending stress of 55 N/mm2 anywhere in the beam. E = 7 x 104 N/mm2. 5. A cantilever of 250 mm x 150 mm steel-I beam 3 m long having moment of inertia of 8 × 107 mm4. Find (a) the point load at the free end (b) the UDL that can run throughout the span to give a maximum deflection of 6 mm. E = 2 × 105 N/mm2. 6. A cantilever beam 2m long is loaded as shown in Fig. Calculate the deflection at the free end if the section is rectangular 100 mm × 200 mm. E = 110 Gpa. 7. A SSB of 6m span carries a concentrated load of 50 KN at 3m from left support. Find the slope at the supports and deflection under the load. EI = 2000 KN-m2 8. A simply supported beam of 10m span is subjected to an UDL of 20 kN/m for the entire length and a concentrated load of 30 kN at 2m from the right support. Determine the slope at the supports and the deflection under the concentrated load in terms of the flexural rigidity E I. 9. A simply supported beam of 10m span carries a point load of 10 kN at its center. It is also subjected to a UDL of 2 kN/m over its entire span. Find the maximum deflection of beam by 1. Double integration method 2. Macaulay's method 3. Moment are method and 4. Conjugate beam method Take E = 200 kN/mm2, I = 200 × 106 mm4 10. A rectangular beam of cast iron 36 mm wide and 80 mm deep is tested on supports 1m apart and shows a central deflection of 3mm under a central point load of 20 KN. Find the Young's modulus of the beam material.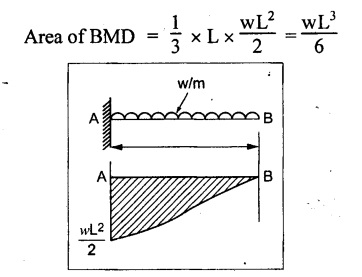
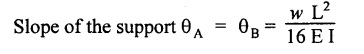
REVIEW QUESTIONS
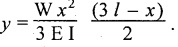
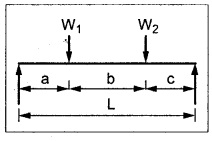
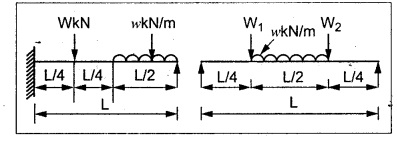
PROBLEMS FOR PRACTICE
Strength of Materials: Unit IV: Deflection of Beams : Tag: : Deflection of Beams - Strength of Materials - Two mark Questions and Answers
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
