Strength of Materials: Unit III: Torsion
Two mark Questions and Answers
Torsion - Strength of Materials
Two mark Questions and Answers: Torsion - Strength of Materials
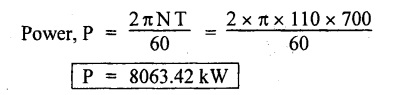
TWO MARK QUESTIONS AND ANSWERS 1. Define Torsion. When a pair of forces of equal magnitude but opposite directions acting on body, it tends to twist the body. It is known as twisting moment or torsional moment or simply as torque. Torque is equal to the product of the force applied and the distance between the point of application of the force and the axis of the shaft. 2. What are the assumptions made in torsion equation? 1. The material of the shaft is homogeneous, perfectly elastic and obeys Hooke's law. 2. Twist is uniform along the length of the shaft. 3. The stress does not exceed the limit of proportionality. 4. The shaft circular in section remains circular after loading. 5. Strain and deformations are small. 3. Write torsional equation. 4. Write down the expression for power transmitted by a shaft. 5. Write down the expression for torque transmitted by hollow shaft. 6. Define Polar modulus. It is the ratio between polar moment of inertia and radius of the shaft. Polar moment of inertia 7. Write the polar modulus for solid shaft and circular shaft. For solid shaft 8. Why hollow circular shafts are preferred when compared to solid circular shafts? 1. The torque transmitted by the hollow shaft is greater than the solid shaft. 2. For same material, length and given torque, the weight of the hollow shaft will be less compared to solid shaft. 9. Write down the equation for maximum shear stress of a solid circular section in diameter 'D' when subjected to torque 'T'. 10. Define Torsional rigidity. Since C, l and J are constant for a given shaft, θ (angle of twist) is directly proportional to T (torque). The term CJ is known as torsional rigidity and it is represented by K. 11. Write an expression for the angle of twist for a hollow circular shaft with external diameter D, internal diameter d, length l and rigidity modulus G. 12. What is the power transmitted by circular shaft subjected to a torque of 700 kN-m at 110 rpm. 13. Calculate the maximum torque that a shaft of 125 mm diameter can transmit, if the maximum angle of twist is 1° in a length of 1.5 m. Take C = 70 × 103 N/mm2. Given data: To find: Maximum torque, Tmax Solution: Torsional equation 1. Derive 2. Derive torque expression for solid shaft. 3. Derive torque expression for hollow shaft. 4. Derive 1. A shaft running at 140 rpm is required to transmit 37.5 kW. If the maximum torque is likely to exceed the mean torque by 25%. Find the diameter of the shaft, if the maximum shear stress is 60 N/mm2. Find also the angle of twist for a length of 2.25 m. Take C = 8 × 10 N/mm2. [Ans: (1) 64.74 mm, (2) 2° 59′] 2. Find the diameter of a solid shaft to transmit 115 kW of power at 225 rpm, f the shear stress is not to exceed 80 N/mm2 and the twist shall not exceed 1° in a length of 3.25m. Take C = 8 × 104 N/mm2. [Ans: 103.7 mm] 3. Find the power that can be transmitted by a 60 mm diameter shaft at 160 rpm if the permissible shear stress is 80 N/mm2 and the maximum torque is 30% greater than the mean torque. [Ans: 43.74 kW] 4. Find the size of a square shaft to transmit 75 kW at 120 rpm if shear stress is not to exceed 50 N/mm2. [Ans: 83 mm × 83 mm] 5. A shaft is 2 m long 60 mm diameter at one end and tapers at a uniform rate to 80 mm diameter at the other end. The larger end is firmly fixed and a torque at 3500 Nm is applied to the smaller end. Find the maximum shear stress and the total angle of twist. Take C = 8 × 104 N/mm2. [Ans: 82.5 N/mm2, 2° 16'] 6. A hollow shaft of diameter ratio 3:5 is required to transmit 600 kW at 110 rpm the maximum torque being 12% greater than the mean. The shearing stress is not to exceed 60 N/mm2 and the twist in a length of 3 m is not to exceed one degree. Find the minimum external diameter of the shaft satisfying these conditions. Take C = 8.4 × 104 N/mm2. [Ans: 171.9 mm]







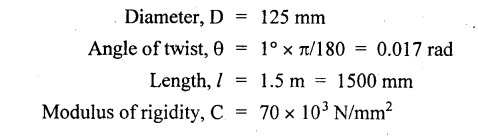 =
=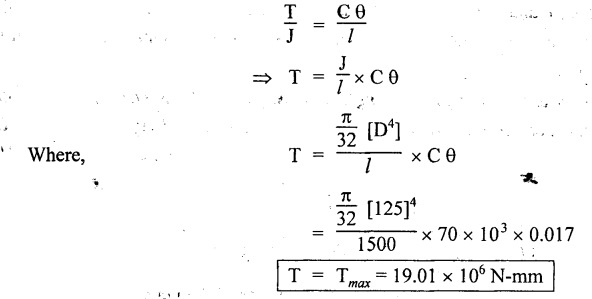
REVIEW QUESTIONS
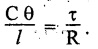
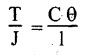
PROBLEMS FOR PRACTICE
Strength of Materials: Unit III: Torsion : Tag: : Torsion - Strength of Materials - Two mark Questions and Answers
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
