Strength of Materials: Unit II: Transverse Loading on Beams and Stresses in Beam
Two mark Questions and Answers
Transverse Loading on Beams and Stresses in Beam - Strength of Materials
Two mark Questions and Answers: Transverse Loading on Beams and Stresses in Beam - Strength of Materials
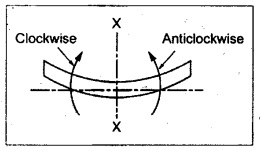
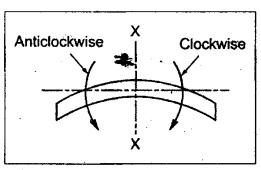
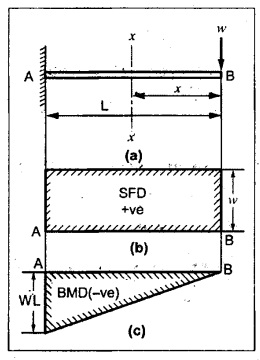
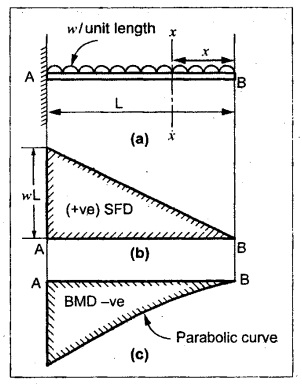
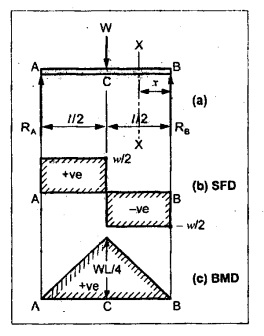
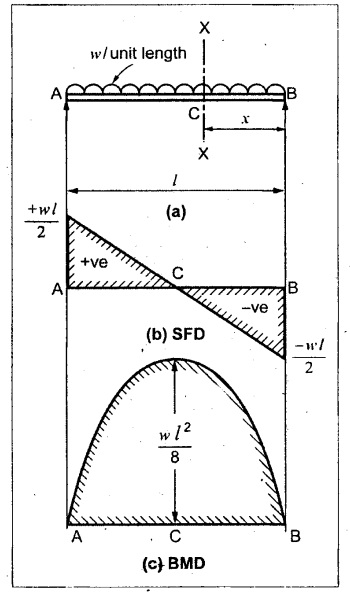
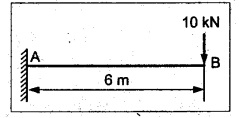
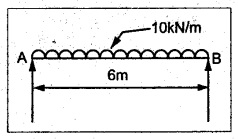
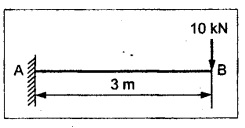
TWO MARK QUESTIONS AND ANSWERS 1. Define Beam. Beam is a structural member which is supported along the length and subjected to external loads acting transversely i.e., perpendicular to the centre line of the beam. Beam is sufficiently long as compared to the lateral dimensions. 2. What is meant by transverse loading on beams? If a load is acting on the beam which is perpendicular to the centre line of it, then it is called transverse loading. 3. How to classify the beams according to its supports? The beam may be classified according to the support as following: (a) Cantilever beam (b) Simply supported beam (c) Over hanging beam (d) Fixed beam and (e) Continuous beam 4. What is cantilever beam? A beam with one end free and the other end fixed is called cantilever beam. 5. What is simply supported beam? A beam supported or resting freely on the supports at its both ends is called simply supported beam which is shown in Figure. 6. What is meant by overhanging beam? If one or both of the end portions are extended beyond the support, then it is called overhanging beam. 7, What are the types of transverse load? A beam may be subjected to the following types of transverse loads, (a) Point or concentrated load. (b) Uniformly distributed load. (c) Uniformly varying loads. 8. What is meant by point or concentrated loads? A load (W) which is acting at a point is called point load. 9. What is uniformly distributed load? If a load which is spread over a beam in such a manner that rate of loading 'w' is uniform through out the length, then it is called as UDL. 10. Define shear force and bending moment at a section. Shear Force: SF at any cross section is defined as the algebraic sum of all the forces acting either side of a beam. Bending Moment: BM at a cross section is the algebraic sum of the moments of all the forces which are placed either side from that point. 11. What is meant by positive or sagging BM? BM is said to be positive or sagging if the moment of the force in the left side of the beam is clockwise or right side of the beam is counter clockwise. Otherwise the beam tends to bend like concave manner. 12. What is meant by negative or hogging BM? BM is said to be negative or hogging if the moment of the forces in the left side of the beam is counter clockwise or right side of the beam is clockwise. Otherwise the beam tends to bend like convex manner. 13. Draw the rough sketch of SF and BM for the beam given below. 14. Draw the rough sketch of SF and BM for the beam given below. 15. What will be the SF and BM diagrams for the simply supported beam of lengh 'L' subjected to central point load 'W"? 16. Draw the SF and BM diagrams for the simply supported beam of length ‘L' subjected to UDL of w/m length throughout its length. 17. When will be the BM is maximum? BM will be maximum when the SF changes its sign. 18. In simply supported beam, the BM at the support is always―――. Zero. 19. What is meant by reaction? The upward force provided by the supports to balance the vertical downward load is called reaction. 20. What is the nature of curve when the beam carrying UDL? The curve follows parabolic relation or parabolic curve. 21. What are the SF and BM diagram for the beam given below? 22. Draw the SFD and BMD for the overhanging beam carrying UDL throughout its length and supported at 'a' distance from end A and 'b' distance from end B. 23. The BM at the support of the overhanging beam is always zero - True/False. False. Since in overhanging beam, the BM always zero at both the ends. 24. Draw the BMD for cantilever beam subjected to an anticlockwise moment at its free end. BM calculation: BM at B = +M (Since +ve for counter clockwise moment) BM at A = +M (BM at both the ends A are same) 25. Define the term point of contraflexure. The point where the BM changes its sign or zero is called the point of contraflexure. 26. What are SF and BM diagrams? SF diagram shows the variation of forces along the length of the beam. BM diagram shows the variation of bending moment along the length of the beam. 27. Draw the SF and BM diagram for a cantilever beam of span 'L' carrying a point load 'W' at a distance of 'a' from free end. SF calculation: SF at C = 0 SF at B = W kN SF at A = W kN BM calculation: BM at C = 0 BM at B = 0. BM at A = w × (L - a) kN - m 28. Write the relation between SF and BM. The rate of change of BM is equal to the SF at the section, dM /dx = -F 29. A cantilever beam of length 5m is acted upon by a force couple of moment 100 kNm at the free end. What is the bending moment at the fixed end? BM calculation: BM at B = + 100 kN-m BM at A = + 100 kN-m (+ve for counter clockwise moment) [Since, couple is always independent of its span] 30. A cantilever beam of length 6m is acted upon by a concentrated load of 10 kN at 2 m from the free end. Calculate the SF and BM at the free end. SF calculation: SF at C = 0 SF at B = 10 KN SF at A = 10 kN BM calculation: BM at C = 0 BM at B = 0 BM at A = 10 × 4 = 40 kN-m ⸫ The SF and BM at the free end are zero. 31. The maximum BM in a SSB of span ‘L' subjected to UDL of w over the entire span is ―――. 32. In SSB, how do you locate the point of maximum bending moment. The BM is maximum when the SF changes its sign or zero. Write the SF equation at that point and equating it to zero we can find out the distance 'x' from one end. Then find the maximum BM at that point by taking moment of all forces left or right from that point. 33. A cantilever of span 4m is subjected to a UDL of 20 kN/m over its entire length. Sketch the BMD for the beam. BM at B = 0 34. A cantilever beam of span 6m is subjected to a point load of 10 kN/m at the free end. What is the maximum BM? BM at A = 0 BM at B = 10 × 6 = 60 kN-m ⸫ The maximum BM = 60 kN-m 35. A beam AB of span 6m is subjected to a UDL of 10 kN/m over the entire span. What is the maximum BM? For this case, BM is maximum at mid span of the beam. Mmax = 10 × 3 × 3/2 = 45 kN-m 36. Calculate the BM at the fixed end of a cantilever beam subjected to a point load of 10 kN at 3m from fixed end. BM at A = 10 × 3 = 30 kN-m The BM at fixed end is 30 kN-m.

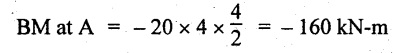
Strength of Materials: Unit II: Transverse Loading on Beams and Stresses in Beam : Tag: : Transverse Loading on Beams and Stresses in Beam - Strength of Materials - Two mark Questions and Answers
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
