Engineering Physics: Unit I: Mechanics
Torque
Definition, Units, Vector diagram, Formula, Derivation
Torque is the turning effect of a force on a body, on which the force acts. The moment of the applied force is called torque. It is represented by the symbol ‘τ’.
Torque (Rotational dynamics)
Torque(τ)
Torque is the turning effect of a force on a body, on which the force acts.
The turning effect of a force depends on
(i) the magnitude of the force and
(ii) the perpendicular distance from the axis of rotation to the line of action of the force
Definition
The moment of the applied force is called torque. It is represented by the symbol ‘τ’.
If F is the force acting on a body at a distance r (Fig. 1.40) then,
Torque = Force × distance
i.e., τ = F × r
The rotational motion comes into picture only when the torque acts on the body.
Torque in vector notation
When a force is applied on a rigid body capable of rotation about some axis, the body rotates about the axis.
The ability of a force to rotate a body about an axis is measured in terms of a quantity called torque.
Consider a body capable of rotation about an axis passing through O. Let a force F act at A, distance 'r’ from O such that the line of action of the force is perpendicular to OA.
The moment of this force F about the axis through O is a measure of the torque. (Fig 1.40)
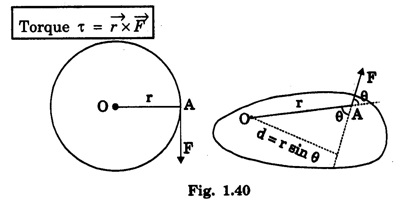
If the direction of the force is inclined at an angle θ with the direction of r, it is measured as the product of the force F and the perpendicular distance from the axis of rotation to the line of action of the force.
∴ Torque = F × ON = F × d = F.r sin θ
This can be expressed in vector form as
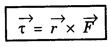
Thus torque is the cross product of force ![]() and the vector
and the vector ![]() between the axis of rotation and the point of application of the force.
between the axis of rotation and the point of application of the force.
It is acting in a direction perpendicular to the plane containing 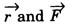 and its direction is given by right hand screw rule.
and its direction is given by right hand screw rule.
If 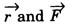 perpendicular to each other τ = rF
perpendicular to each other τ = rF
(⸪ θ = 90° and sin θ = 1)
Unit of Torque
Newton - metre (Nm)
Laws of motion applied to rotatory motion
1. A rotating body tends to rotate continuously and uniformly about a fixed axis unless it is acted upon by an external torque.
2. The rate of change of angular momentum is equal to the external torque applied and acts in the direction of torque
3. When a body exerts a torque on another body, the second body exerts an equal and opposite torque on the first body about the same axis of rotation.
Relation between torque and angular momentum
Consider a rigid body capable of rotation about the axis. Let I be the moment of inertia of the body about that axis. Let a constant torque τ acting on it changes its angular velocity from ω0, ω in time 't'.
Torque = rate of change of angular momentum
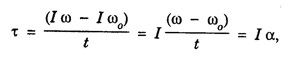
where α is the angular acceleration.
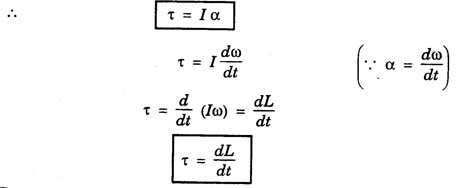
Engineering Physics: Unit I: Mechanics : Tag: : Definition, Units, Vector diagram, Formula, Derivation - Torque
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
