Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations
Thermodynamic Relations
Exact Differentials, Theorem
For solving the problems in engineering, the evaluation of thermodynamic properties is essential.
THERMODYNAMIC RELATIONS For solving the problems in engineering, the evaluation of thermodynamic properties is essential. Thermodynamic properties are pressure (p), temperature (T), volume (v), internal energy (U), enthalpy (h), entropy (s), Helmholtz function (a) and Gibbs function (g). Out of the above eight basic thermodynamic properties, only three thermodynamic properties i.e, pressure, temperature and volume are directly measurable while the other properties are evaluated in terms of these measurable properties. These relations are mainly developed for the system having constant chemical composition. These systems are subjected to non-flow or steady flow processes. Mainly, the change in these properties can be determined in terms of non-measurable and measurable thermodynamic properties by mathematical interrelations. Theorem 1 The relation between variables, x, y and z can be expressed as a function of other two. For example, z can be written as z = f(x, y) By partial derivation, the differential function of two variables is equal to the sum of the partial derivatives by changing one variable at one time and the other one remains constant. By comparing equations (5.40) and (5.41), it can be written as It is the main condition of exact differential. Theorem 2 Any one of x, y and z can be written as a function of f and any one of x, y and z. If x = x (f, y) By mathematical rule, Theorem 3 Among three variables x, y and z, any one is considered as a function of other two. Let us assume x = x (y, z) By mathematical rule, Taking the inverse on both sides, By the rearrangement, Instead of assuming x, y and z, we can assume that pressure (p), volume (v) and temperature (T)1. Exact Differentials

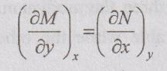


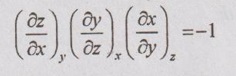


Engineering Thermodynamics: Unit V: Gas Mixtures and Thermodynamic Relations : Tag: : Exact Differentials, Theorem - Thermodynamic Relations
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
