Engineering Physics: Unit I: Mechanics
Theorems on moment of inertia (MI)
Theorem of Parallel axes, Perpendicular axes
There are two important theorems which help to find the moment of inertia of a body about some other axis if moment of inertia about any symmetrical axis of the body is given.
THEOREMS ON MOMENT OF INERTIA (MI) There are two important theorems which help to find the moment of inertia of a body about some other axis if moment of inertia about any symmetrical axis of the body is given. These are called theorems of parallel and perpendicular axes. They are 1. Parallel axes theorem and 2. Perpendicular axes theorem Statement The moment of inertia of a body about any axis is equal to the sum of its moment of inertia about a parallel axis passing through its centre of gravity of the body and the product of its mass of the body with the square of the distance between the two axes. Explanation Let G be the centre of gravity of a rigid body of mass M. Let AB be an axis parallel to axis CD. (Fig 1.23), Let a be the distance between the axes. If I and IG are the moments of inertia of the body about the axes AB and CD respectively, then by the theorem of parallel axes, Consider a particle of mass m at a distance r from CD. M.I. of this particle about the axis CD = mr2 ∴ M.I. of the whole body about CD, IG = Σ mr2 M.I. of the particle about the axis AB = m (r + a)2 ∴ M.I. of the whole body about AB, I = Σ m (r + a)2 I = Σ m (r2 + a2 + 2ar) = Σ mr2 + a2Σ m + 2a Σ mr ie, I = IG + Ma2 + 2a Σ mr Σ mr represents the algebraic sum of the moments of all the mass particles of the body about an axis through the centre of gtavity of the body. Since the body always balances about an axis through its centre of gravity. Σ mr should be zero. Therefore, Statement It states that the moment of inertia of a plane lamina about an axis perpendicular to its plane is equal to the sum of the moments of inertia of the plane lamina about any two mutually perpendicular axes in its own plane and intersecting each other at the point where the perpendicular axis passes through it. Explanation Let OX and OY be two mutually perpendicular axes in the plane of the lamina, intersecting each other at the point O. OZ is the axes perpendicular to both OX and OY. (Fig 1.24) Let Ix and Iy be the moments of inertia of the lamina about the axis OX and OY respectively. If Iz is the moment of inertia about the axis OZ, passing through O and perpendicular to the plane of the lamina, then by the theorem of perpendicular axes, Proof Consider a particle P of the lamina of mass m at a distance r from O. Let x and y be the distances of the particle from OY and OX respectively. M.I. of this particle about OX = my2 M.I. of the entire lamina about OX, Ix = Σ my2 Similarly M.I. of the lamina about OY, Iy = Σ mx2 M.I. of the lamina about OZ axis through O and perpendicular to the plane of the lamina, Iz = Σ mr2 ... (1) But r2 = x2 + y2 ... (2) Substituting eqn (2) in eqn .(1), we have Iz = Σ m (x2 + y2) Iz = Σ mx2 + Σ my2 Iz = Iy + Ix The moment of inertia of a continuous homogeneous body (Rigid body) with definite geometrical shape can be calculated as follows. • Find the moment of inertia of an infinitesimal element of the body about the given axis. i.e., Multiply the mass dm of the element by x2, the square of the distance from the given axis. • Then, integrate the expression between the limits to get moment of inertia of whole of the body. where the integral is taken over the whole body. In fact some times the theorems parallel and perpendicular axes are also used to calculate the moment of inertia.1. Theorem (Principle) of Parallel axes
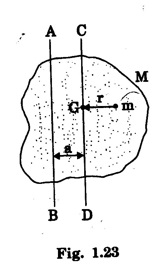
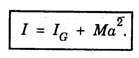 Proof
Proof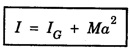
2. Theorem (Principle) of Perpendicular axes
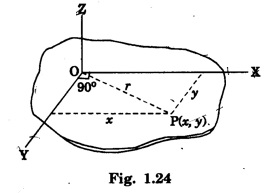
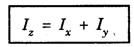
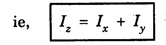
Calculation of Moment of Inertia of a body
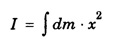
Engineering Physics: Unit I: Mechanics : Tag: : Theorem of Parallel axes, Perpendicular axes - Theorems on moment of inertia (MI)
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
