Matrices and Calculus: Unit III: Functions of Several Variables
Taylor's Expansion for Function of Two Variables
Theorem, Worked Examples, Exercise with Answers
Taylor's formula gives polynomial approximation to a function of two variables about a given point.
TAYLOR'S EXPANSION FOR FUNCTION OF TWO VARIABLES The Taylor's series expansion of a single variable function f(x) in a neighbourhood of a point a is which is an infinite power series in h. Maclaurin's series is These ideas are extended to a function f(x, y) of two independent variables x, y. We state the theorem. Let f(x, y) be a function of two independent variables x, y defined in a region R of the xy-plane and let (a, b) be a point in R. Suppose f(x, y) has all its partial derivatives in a neighbourhood of (a, b) then 1. Put x = a + h, y = b + k, then h = x - a, k = y - b ⸫ the Taylor's series can be written as This series is known as the Taylor's expansion of f(x, y) in the neighbourhood of (a, b) or about the point (a, b). 2. Putting a = 0, b = 0 we get the expansion of f(x, y) in the neighbourhood of (0, 0) This is called Maclaurin's series for f(x, y) in powers of x and y. Note Taylor's formula gives polynomial approximation to a function of two variables about a given point. Example 1 Expand Solution We know the expression of f(x, y) about the point (a, b) as Taylor's series is Here (a, b) = (1, 1) Example 2 Expand sin (xy) in powers of (x - 1) and Solution We know Taylor's expansion about the point (a, b) is we have f(x, y) = sin(xy) At the point (1, π/2) Example 3 Expand ex cos y near the point (1, π/4) by Taylor's series as far as quadratic terms. Solution We know Taylor's series about the point (a, b) is Example 4 Expand ex loge (1 + y) in powers of x and y upto terms of third degree. Solution Required the expansion in powers of x and y and so Maclaurin's series is to be used. We know f(x, y) = ƒ(0,0) + [x ƒx (0, 0) + y ƒy(0, 0)] Given f(x, y) = ex log (1 + y) At the point (0, 0) Example 5 Expand x2 y + 3y - 2 in powers of x - 1 and y + 2 using Taylor's theorem. Solution We know Here (a, b) = (1, −2) Note Since the given function is 3rd degree in x, y, the expansion terminates. Example 6 If f(x, y) = tan-1(xy) compute an approximate value of f(0.9, -1.2) Solution We shall use Taylor's series to find the approximate value. The point (0.9, −1.2) is close to the point (1, −1). So we shall find the Taylor's series about (1, -1). Here (a, b) = (1, −1) Put x =0.9, y = -1.2 Note We have approximated tan-1 xy by a second degree polynomial in x and y. Using this polynomial we have found the approximate value of f(0.9, -1.2) = -0.8229 But by direct computation f(0.9, −1.2) = tan-1(−1.08) = tan-1 1.08 = -0.8238 correctly upto 4 decimal places. The error is only 0.0009, which is negligible. Example 7 Find the Taylor series expansion of ex sin y at the point Solution Let f(x, y) = ex sin y We know Taylor series expansion of f(x, y) about (a, b) is Example 8 Expand ex cos y in powers of x and y at (0, 0) upto third degree term, by Taylor's theorem. Solution Let f(x, y) = ex cos y We know that Taylor's series about (a, b) is Here (a, b) = (0, 0) Taylor's series about (0, 0) is Example 9 Expand exy in powers of (x − 1) and (y - 1) upto third degree terms, by Taylor's series. Solution Let f(x, y) = exy The Taylor's series for f(x, y) about (a, b) is Here (a, b) = (1, 1) ⸫ the Taylor's series expansion for exy about (1, 1) is Example 10 Obtain the Taylor series of x3 + y3 + xy2 in powers of (x − 1) (y − 2) Solution Let f(x, y) = x3 + y3 + xy2 The Taylor series about (a, b) is Hence (a, b) = (1, 2) ⸫ Taylor's series is Example 11 Expand ex sin(y) in powers of x and y up the third degree terms. Solution Let f(x, y) = ex sin y We know the Taylor's series about (0, 0) is Here the point is (0, 0) We have ⸫ the Taylor's series is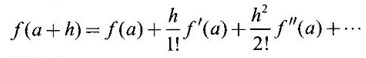
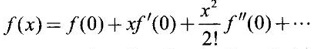
Theorem 3.4.1 Taylor's theorem

Modified forms

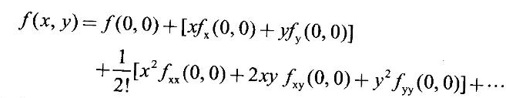
WORKED EXAMPLES
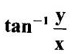 about (1, 1) upto the second degree terms.
about (1, 1) upto the second degree terms.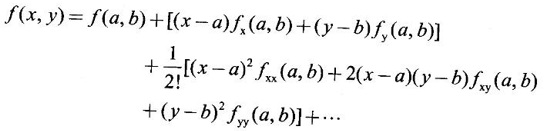
 upto the second degree terms.
upto the second degree terms.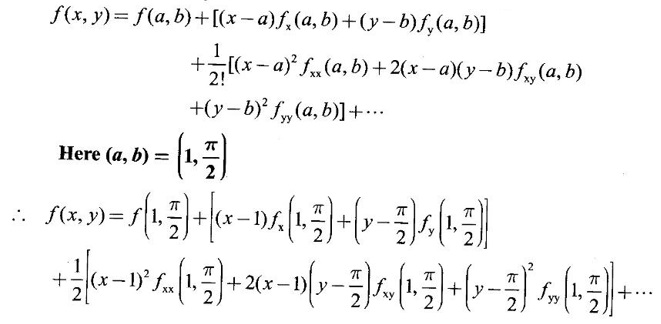
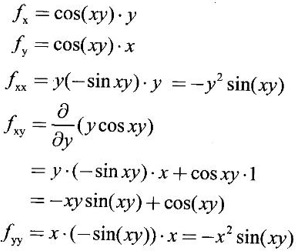
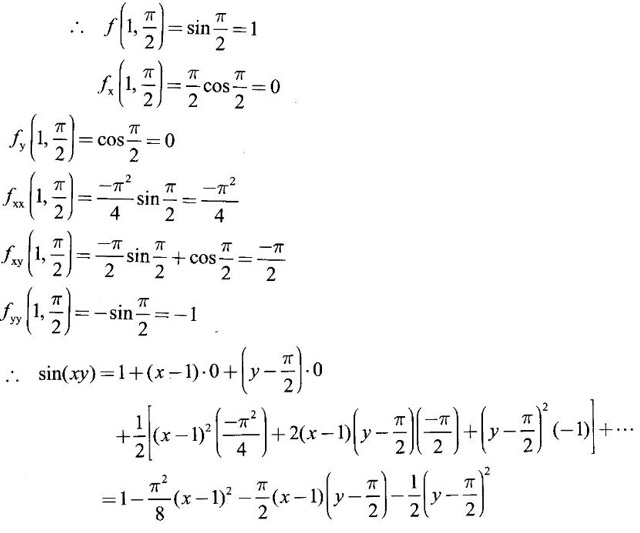

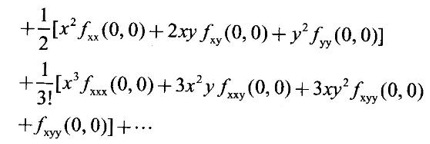
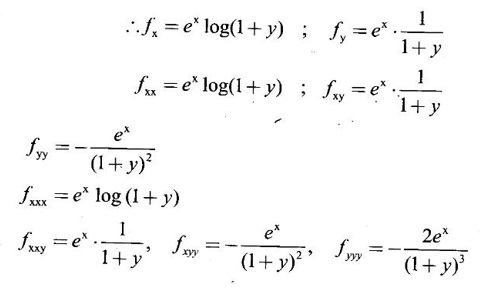
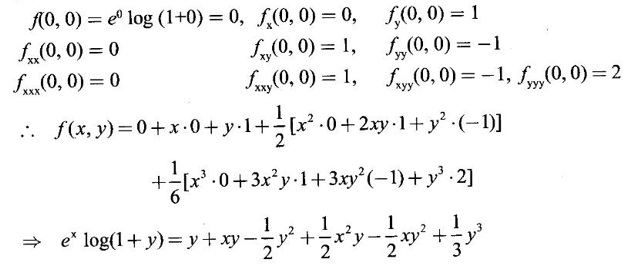
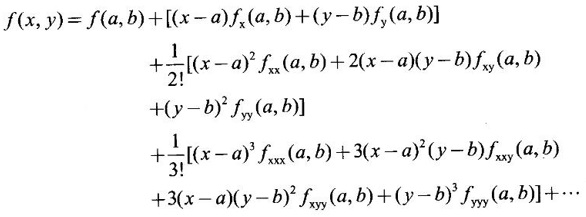
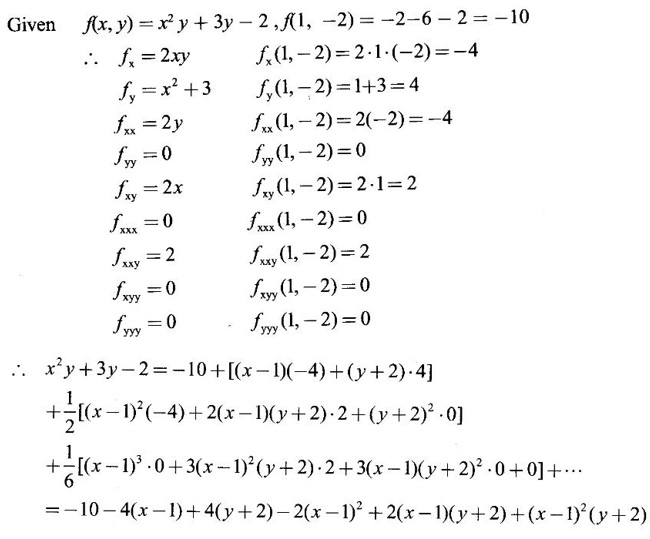

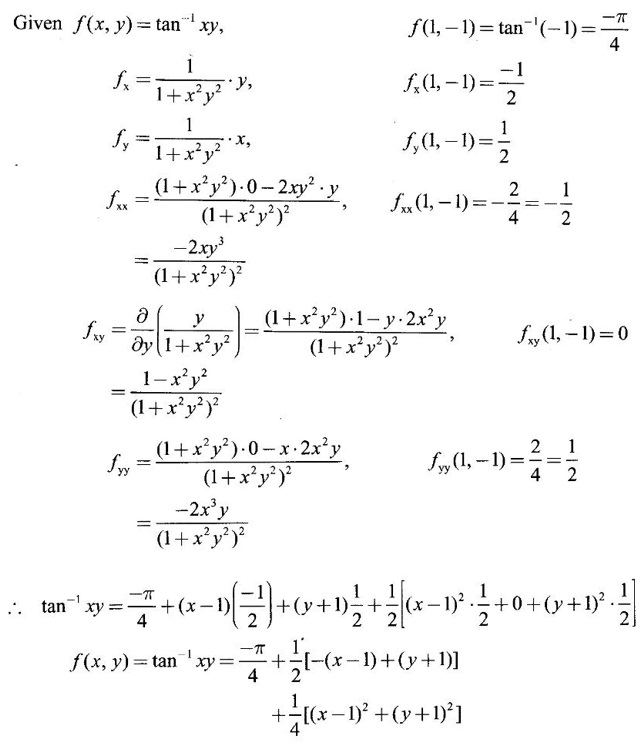
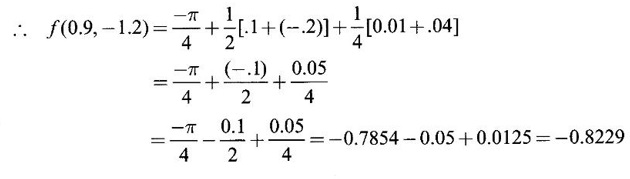
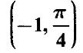 upto 3rd degree terms.
upto 3rd degree terms.
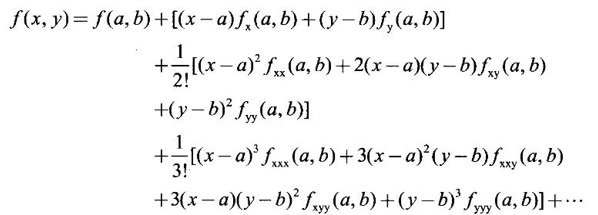
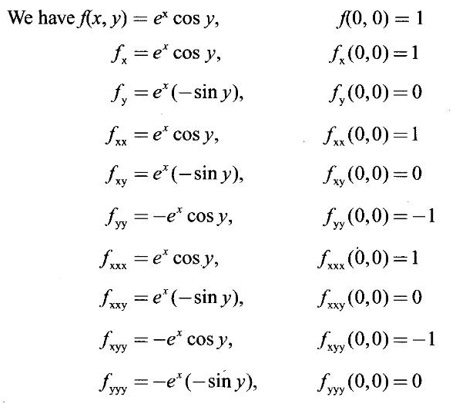
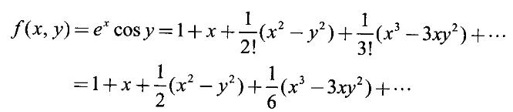


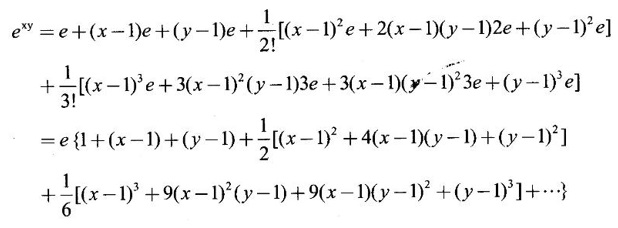
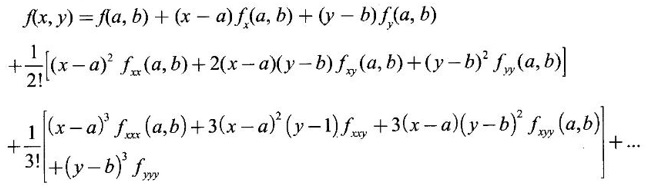
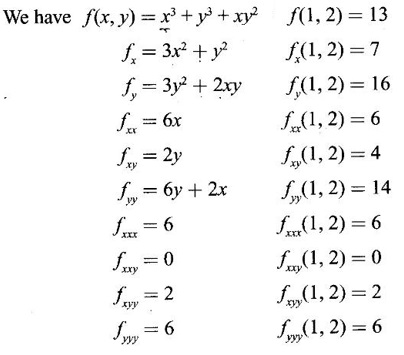
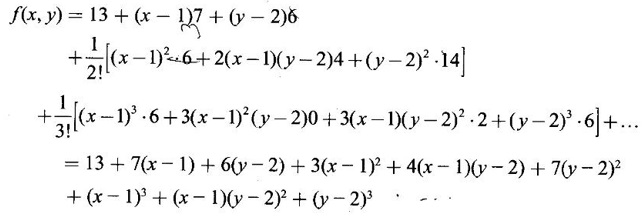

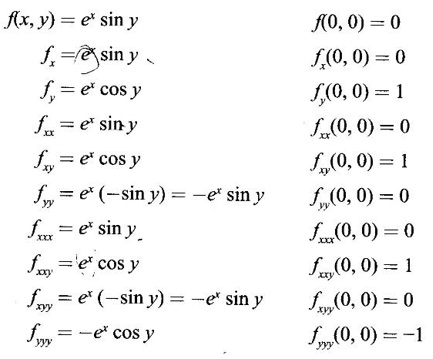
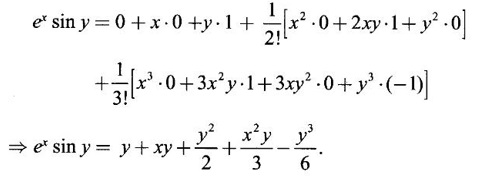
EXERCISE 3.4

ANSWERS TO EXERCISE

Matrices and Calculus: Unit III: Functions of Several Variables : Tag: : Theorem, Worked Examples, Exercise with Answers - Taylor's Expansion for Function of Two Variables
Related Topics
Related Subjects
Matrices and Calculus
MA3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
