Strength of Materials: Unit IV: Deflection of Beams
Strain Energy
Deflection of Beams - Strength of Materials
When an elastic material is deformed due to application of external force, internal resistance is developed in the material of the body.
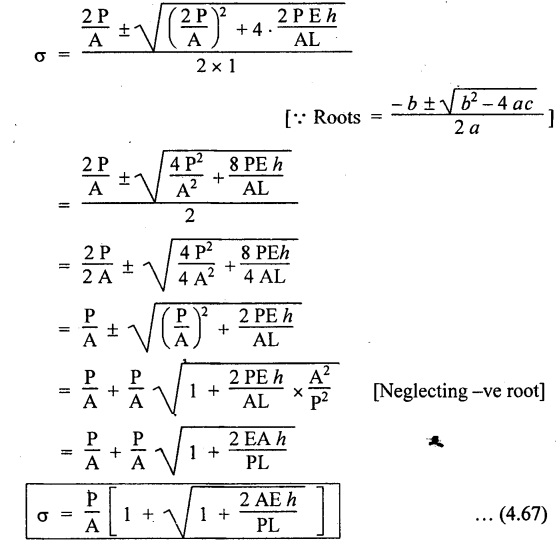
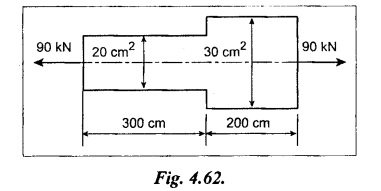
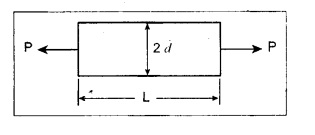
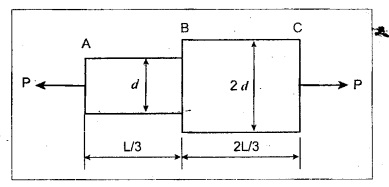
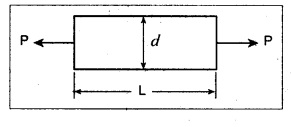
STRAIN ENERGY When an elastic material is deformed due to application of external force, internal resistance is developed in the material of the body. Due to deformation, some work is done by the internal resistance developed in the body, which is stored in the form of energy. This energy is known as strain energy. It is expressed in N-m. The total strain energy stored in the body is generally known as resilience. The maximum strain energy that can be stored in a material within its elastic limit is known as proof resilience. It is the proof resilience of the material per unit volume. Modulus of resilience = Proof resilience / Volume of the body It is the most common and practical way of loading a body in which the loading starts from zero and increases gradually till the body is fully loaded. Now consider a metallic bar subjected to a gradual load. Fig.4.59 shows load extension diagram of a body under tensile test upto elastic limit. The tensile load P increases gradually from zero to value of A and the extension of the body increases from zero to value of x. Let x = Extension of the body. P = "Gradually applied load. A = Cross-sectional area. L = Length of the body. V = Volume of the body. E = Young's modulus. U = Strain energy stored in the body. σ = Stress induced in the body. Work done by the load = Area of load extension curve = Area of ∆OBC We know that, Load, P = Stress × Area We know that, Work done by the load is equal to energy stored in the body, When the load is applied suddenly to the bar, the load is constant throughout the process of the deformation of the bar. Consider a bar subjected to a sudden load. Let, P = Load applied suddenly L = Length of the bar A = Area of cross section V = Volume of the bar = A × L E = Young's modulus x = Extension of the bar σ = Stress induced by suddenly applied load U = Strain energy stored We know that, Work done by the load = Load × Extension = P × x We know that, Energy stored in the body = Work done by the load From the above equation, we know that the maximum stress produced due to the suddenly applied load is equal to twice the stress produced when same load is applied gradually. Sometimes in factories and workshops, the load with impact is applied on a body. Consider a vertical rod fixed at the upper end and having a collar at lower end as shown in Fig.4.60. Let the load be dropped from a height on the collar. Due to this impact load, there will be some extension in the rod. Let, P = Load applied with impact. L = Length of the rod. A = Cross-sectional area. V = Volume of the rod = A × L h = Height through which the load will fall before impacting the collar of the bar. δL = Extension of the rod due to the load P. E = Modulus of elasticity of the rod material. σ = Stress induced due to impact loading. We know that, Work done, W = Load × Distance moved The strain energy stored by the rod, We know that, work done is equal to strain energy stored. Solving this quadratic equation, Once the stress σ is obtained, the corresponding instantaneous deformation (8L) can be calculated. Note: If 8L is very small as compared to h, then Work done by load = P•h We know that, work done is equal to strain energy stored. Consider a cube ABCD of length L, fixed at the bottom face AB as shown in Fig.4.61. Let, q = Shear stress produced. ϕ = Shear strain. C = Modulus of rigidity. P = Force applied torsionally on the face DC We know that, Work done by gradually applied shear force, We know that, Work done is equal to the strain energy stored. Example 4.16 A circular bar of 60 mm diameter and 7 m long subjected to gradually applied load of 80 kN. Calculate (i) stretch in the rod, (ii) stress in the rod, (iii) strain energy absorbed by the rod. Take E = 2 × 105 N/mm2. Given: To find: 1. Stretch in the rod. 2. Stress in the rod. 3. Strain energy absorbed by the rod. Solution: Volume of the rod, V = A × L = 2827.4 × 7000 V = 19792033.7 mm3 Let x = Stretch (or) extension in the rod σ = Stress in the rod. U = Strain energy absorbed by the rod. We know that, (ii) Stretch (or) extension is given by, (iii) Strain energy absorbed by the rod is given by, Result: (i) Stretch in the rod, x = 0.99 mm (ii) Stress in the rod, σ = 28.29 N/mm2 (iii) Strain energy absorbed by the rod, U = 39.6 N-m Example 4.17 A steel bar 20 mm in diameter is pulled axially by a force of 15 kN. If the bar is 400 mm long, calculate the strain energy stored per unit volume of the bar and total strain energy stored by the bar. Take E = 2 × 105 N/mm2. Given: Diameter of the bar, D = 20 mm Load, P 15 kN = 15000 N Length, L = 400 mm E = 2 × 105 N/mm2 To find: 1. Strain energy stored per unit volume of the bar. 2. Total strain energy stored by the bar. Solution: Result: (i) Strain energy stored per unit volume of the bar = 5.6 × 10-3 N-mm/mm3 (ii) Total strain energy stored by the bar = 715.98 N-mm Example 4.18 A bar of 1500 m2 area and 4000 mm long is subjected to sudden application of a tensile load of unknown magnitude. The extension of the bar due to suddenly applied load is 2 mm. Calculate instantaneous stress produced and suddenly applied load. Take E = 2 × 105 N/mm2. Given: Area of the bar, = 1500 mm2 A Length of the bar, L = 4000 mm Extension due to suddenly applied load, x = 2 mm Young's modulus, E = 2 × 105 N/mm2 To find: 1. Instantaneous stress (σ). 2. Load applied suddenly (P). Solution: Instantaneous stress: The extension x is given by Suddenly applied load: The stress produced is given by, Result: 1. Instantaneous stress produced, σ = 100 N/mm2 2. Load applied suddenly, P = 75 kN Example 4.19 A uniform metal bar has a cross-sectional area of 900 mm2 and a length of 2 m with an elastic limit of 200 N/mm2. What is the proof resilience. Find also the maximum value of applied load which may be suddenly applied without exceeding the elastic limit. Calculate the value of gradually applied load which will produce the same extension as that produced by the above suddenly applied load. Take E = 2 × 105 N/mm2. Given: A = 900 mm2 L = 2 m = = 2000 mm; Stress at elastic limit, σc = 200 N/mm2 To find: 1. Proof resilience. 2. Value of suddenly applied load. 3. Value of gradually applied load. Solution: Result: 1. Proof resilience = 180 kN 2. Suddenly applied load, PS = 90 KN 3. Gradually applied load, P = 180 kN Example 4.20 A tension bar is made of two parts. The length of first part is 300 cm and area is 20 cm2 while the second part is of length 200 cm and area 30 cm2. An axial load of 90 kN is gradually applied. Find the total strain energy produced in the bar and compare this value with that obtained in a uniform bar of same length and having same volume under same load. Take E 2 × 105N/mm2. Given: Length of first part, L1 = 300 cm = = 3000 mm Area of first part, A1 = 20 cm2 = 2000 mm2 Volume of first part, V1 = A1 × L1 = 2000 x 3000 = 6 × 106 mm3 Length of second part, L2 = 200 cm = 2000 mm Area of second part, A2 = 30 cm2 = 3000 mm2 Volume of second part, V2 = A2 × L2 = 3000 × 2000 = 6 × 106 mm3 Axial gradual load, P = 90 kN = 90000 N ; E = 2 × 105 N/mm2 To find: 1. Total strain energy produced in the bar. 2. To compare strain energy produced in this bar and uniform bar. Solution: Total strain energy produced in the bar Strain energy stored in a uniform bar: Result: 1. Total strain energy produced in the bar, U = 43.8 N-m 2. Ratio of strain energy Example 4.21 Two bars each of length L and of the same material are subjected to the same axial tensile force P. The first bar has uniform diameter 2 d and second bar has diameter d for length L/3 and a diameter 2d for remaining length. Compare the strain energies for the two bars. Given: Length of each bar = L Diameter of 1st bar = 2 d Diameter of 2nd bar = d for length L/3, 2 d for remaining length To find: Compare strain energies of two bar. Solution: First bar: Second bar: (ii) Analysis of the first bar: (ii) Analysis of second bar: Result: The ratio of strain energies of two bars = 1/2 Example 4.22 Two bars each of length L and of the same material are subjected to the same axial tensile force P. The first bar has uniform diameter d and second bar has diameter d for length L/2 and a diameter d/2 for remaining length. Compare the strain energy stored by two bars. Given: Length of each bar = L Diameter of first bar = d Diameter of second bar = d for length L/2 and d/2 for remaining length. To find: Compare strain energies of two bars. Solution: First bar: Second bar: Analysis of the first bar: Analysis of second bar: Result: Ratio of strain energies of two bars = 2/5 Example 4.23 A weight of 20 kN falls by 40 mm on a collar rigidly attached to a vertical bar 5000 mm long and 2000 mm2 in section. Find the instantaneous expansion of the bar. Take E = 310 GPa. Given: Falling weight, P = 20 kN = 20,000 N Falling height, h = 40 mm; Length of bar, L = 5000 mm; Area of bar, A = 2000 mm2; E = 310 GPa = 310 × 109 N/m2 = 310 × 103 N/mm2 = 3.1 × 105 N/mm2 To find: Instantaneous expansion of the bar Solution: We know that, when the load is applied with impact, Result: Instantaneous expansion of the bar, δL = 3.757 mm Example 4.24 An object of weight 200 N, falls by gravity a vertical distance of 6 m when it is suddenly stopped by a collar at end of a vertical rod of length 20m and diameter 30 mm. The top of the bar is rigidly fixed to a support. Calculate the maximum stress and strain induced in the bar due to impact. Take E = 2 × 105 N/mm2. Given: Falling weight (or) load, P = 200 N To find: Maximum stress and strain induced in bar. Solution: We know that, when the load is applied with impact, Result: 1. Maximum stress, σ = 130.582 N/mm2 2. Maximum strain, e = 6.529 × 10-4 Example 4.25 A load of 200 N falls through a height of 20 mm onto a collar rigidly attached to the lower end of a vertical bar 2000 mm long and of 1.5 cm2 cross sectional area. The upper end of vertical bar is fixed. Find (i) Maximum instantaneous stress. (ii) Maximum instantaneous elongation. (iii) Strain energy. Take E = 2 × 105 N/mm2 Given: Impact load, P = 200 N Height, h = 20 mm Length of bar, L = 2000 mm Area of bar, A = 1.5 cm2 = 1.5 × 102 mm2 = 150 mm2 Volume, V =A × L = 150 × 2000 = 3,00,000 mm3 Modulus of elasticity, E = 2 × 105 N/mm2 To find: (i) Maximum instantaneous stress. (ii) Maximum instantaneous elongation. (iii) Strain energy. Solution: Result: (i) Maximum instantaneous stress, σ = 74.37 N/mm2 (ii) Maximum instantaneous elongation, δL = 0.743 mm (iii) Strain energy stored, U = 4148 N-mm Example 4.26 A load of 150 N falls by gravity of vertical distance of 4 m, when it is suddenly stopped by a collar at the end of a vertical rod of length 50 cm and diameter 30 mm. The top of bar is rigidly fixed to a ceiling. Calculate maximum stress and strain induced in the bar. Take E = 2 × 105 N/mm2. Given: To find: Maximum stress and strain induced. Solution: We know that, when the load is applied with impact, Result: Example 4.27 An unknown weight falls through a height of 1 cm on a collar rigidly attached to lower end of a vertical bar 5000 mm long and 600 mm2 in rod is to be 0.002 m, what is the of the unknown weight. Take section. If the maximum extension of the corresponding stress and magnitude E = 2 × 105 N/mm2. Given: To find: Stress and magnitude of unknown weight. Solution: We know that, When the load is applied with impact, Result: (i) Stress, σ = 80 N/mm2 (ii) Magnitude of unknown weight P = 4000 N Example 4. 28 A 20 mm diameter mild steel bar of length 15 m is stressed by a weight of 200 N dropping freely through 20 mm before commencing to stretch the bar. Find the maximum instantaneous stress and elongation produced in the bar. Take E = 2 × 105 N/mm2 Given: Diameter of the bar, d = 20 mm Load, P = 200 N Length of bar, L = 1.5 m 1500 mm Height, h = 20 mm; E = 2 × 105 N/mm2 To find: (i) Maximum instantaneous stress in the bar. (ii) Elongation in the bar. Solution: When load is applied with impact, Result: (i) Maximum stress in bar, σ max = 58.91 N/mm2 (ii) Maximum elongation, δL = 0.441 mm Example 4.29 A rod 20 mm in diameter is stretched 4 mm under a steady load of 20 kN. What stress would be produced in bar by a weight of 700 N, falling through a distance of 75 mm. The value of E = 2.1 × 105 N/mm2. Given: To find: Stress produced in the bar. Solution: We know that, When the load is applied with impact, Result: Stress produced in the bar, σ = 75.19 N/mm2 Example 4.30 A vertical bar 6 m long and of 3000 mm2 cross sectional area is fixed at the upper end and has a collar at the lower end. Determine the maximum stress induced when a weight: (i) 2000 N falls through a height of 300 mm on collar. (ii) 40 kN falls through a height of 10 mm on collar. Take E = 2 × 105N/mm2. Given: Length of bar, L = 6 m = 6000 mm Area of bar, A = 3000 mm2 To find: Maximum stress induced. Solution: Case (i): Falling weight = P1 = 2000 N; Height = h1 = 300 mm Small weight will produce small extension of the bar. So, the extension of the bar will be negligible as compared to the height. Case (ii): Falling weight = P2 = 40000 N; Height = h2 = 10 mm Large weight will produce large extension of the bar. So, the extension of the bar is not negligible as compared to the height. Result: Example 4.31 A weight W falls a distance h before beginning to stretch a bar of length I and a cross-sectional area A. Derive expression for the maximum stress induced in the bar when, (a) the maximum extension is negligible when compared with h. (b) the maximum extension is of the same order as h. (c) A bqr 2000 mm long, 60 mm diameter hang vertically and has a collar securely attached to the lower end. Find the maximum stress induced (i) when a weight of 2000 N falls by 20 cm on the collar. (ii) when a weight of 20,000 N falls by 25 mm on the collar. Take E = 2.1 × 105 N/mm2. Given: Length of rod, L = 2000 mm; Diameter of rod, d = 60 mm; E = 2.1 × 105 N/mm2 To find: Expression for maximum stress induced for above two cases. Solution: We know that, (a) When maximum extension is small compared with h: (b) When maximum extension is of same order as h: The above quadratic equation is solved as Case (i): P1 = 2000 N; h1 = 200 mm The maximum extension being small compared with h. Case (ii): P2 = 20,000 N; h2 = 25 mm Extension is not negligible when compared to h, since load is large. i.e., 20,000 N. Result: Maximum stresses Case (i): σ = 172.36 N/mm2 Case (ii): σ = 199.91 Example 4.32 A cage weighing 60 kN is attached to the end of a steel wire rope. It is lowered down a mine shaft with a constant velocity of 1 m/s. What is maximum stress produced in the rope when its supporting drum is suddenly jammed? The free length of the rope at the moment of jamming is 15 m, its net cross sectional area is 25 cm2, and E = 2 × 105 N/mm2. The self-weight of the wire rope may be neglected. Given: Weight, W = 60 kN = 60000 N; Velocity, V = 1 m/s; Free length, L = 15 m = 15000 mm; E = 2 × 105 N/mm2; Area, Ab = 25 cm2 = 2500 mm2 To find: Maximum stress produced in the rope. Solution: This energy is absorbed or stored by the rope We know that, K.E of the cage = Energy stored in the rope Result: Maximum stress produced in the rope, σ = 180.61 N/mm2 Example 4.33 A vertical die fixed rigidly at the top end consist of a steel rod 3 m long and diameter 20 mm encased throughout in a brass tube 30 mm internal diameter and 40 mm external diameter. The rod and the casing are fixed together at both ends. The compound rod is suddenly loaded in tension by a weight of 20 kN falling freely through 4 mm before being arrested by the die. Calculate the maximum stress in steel and brass. Take ES = 2 × 105 N/mm2; E = 1 × 103 N/mm2 Given: Steel rod: Length of bar, L = 3 m = 3000 mm; Diameter dS = 20 mm Brass tube: Internal diameter = 30 mm; External diameter = 40 mm; Weight, P = 20 kN = 20000 N; Height, h = 4 mm; Es = 2 × 105 N/mm2; Eb = 1 × 105 N/mm2 To find: Maximum stress induced in steel and brass. Solution: Since elongation of the steel and brass tube are equal, Strain in steel = Strain in brass Equating loss in potential energy of the load to strain energy absorbed by the steel rod and brass tube. Result: Stress in steel bar, σs = 172.72 N/mm2 Stress in brass tube, σb= 86.36 N/mm21. RESILIENCE
2. PROOF RESILIENCE
3. MODULUS OF RESILIENCE
4. EXPRESSION FOR STRAIN ENERGY STORED IN A BODY WHEN LOAD IS APPLIED GRADUALLY



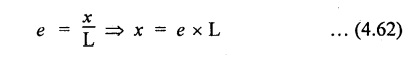
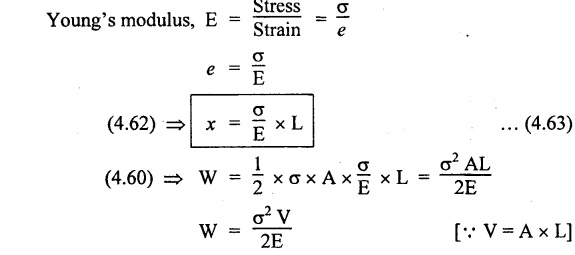

5. EXPRESSION FOR STRAIN ENERGY STORED IN A BODY WHEN THE LOAD IS APPLIED SUDDENLY
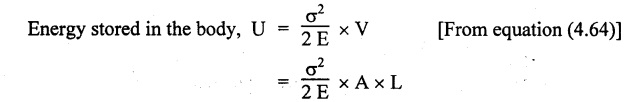

6. EXPRESSION FOR STRAIN ENERGY STORED IN A BODY WHEN THE LOAD IS APPLIED WITH IMPACT
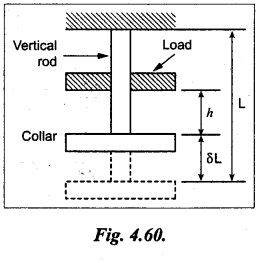
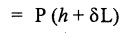
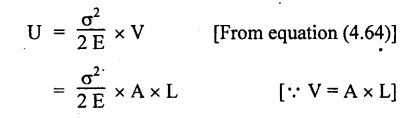


7. EXPRESSION FOR STRAIN ENERGY STORED IN A BODY DUE TO SHEAR STRESS



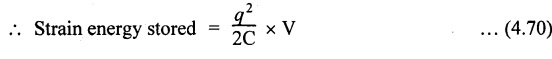
8. SOLVED PROBLEMS





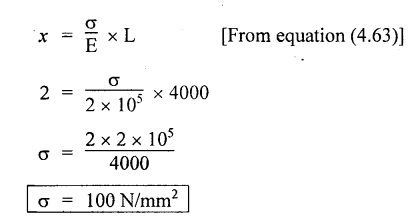



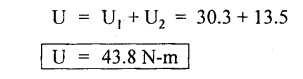
















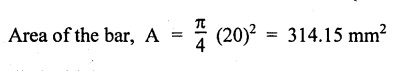




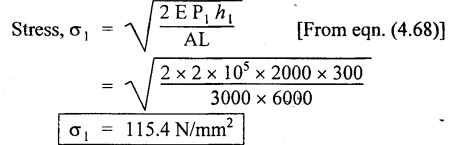
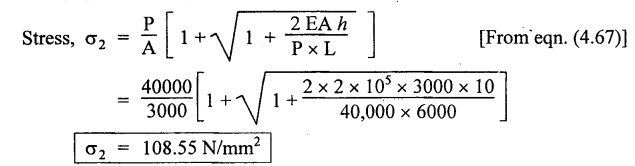
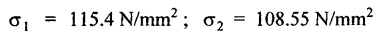
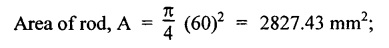
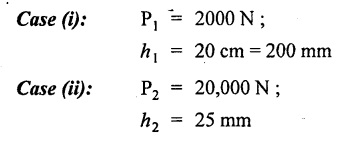




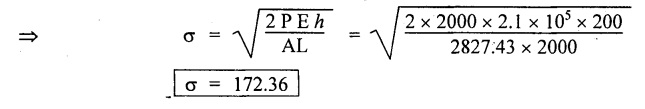
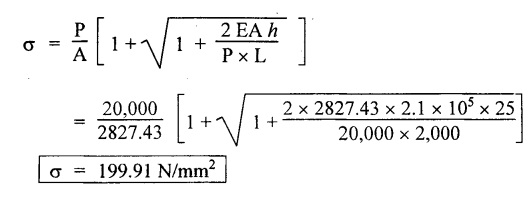
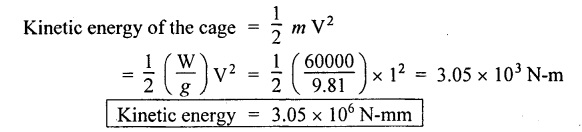
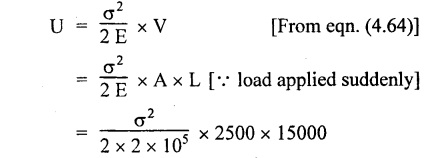
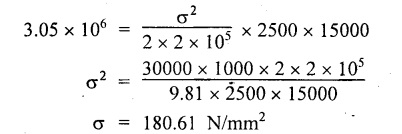



Strength of Materials: Unit IV: Deflection of Beams : Tag: : Deflection of Beams - Strength of Materials - Strain Energy
Related Topics
Related Subjects
Strength of Materials
CE3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
