Transforms and Partial Differential Equations: Unit III: Applications of Partial Differential Equations
Steady state solution of two dimensional equation of heat conduction (Heat flow equations) (excluding insulated edges)
Solved Example Problems
When the heat flow is along curves, instead of straight lines, the curves lying in parallel planes, the flow is called two dimensional.
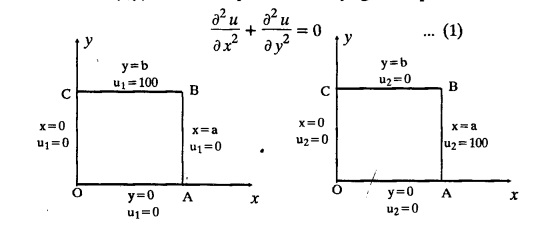
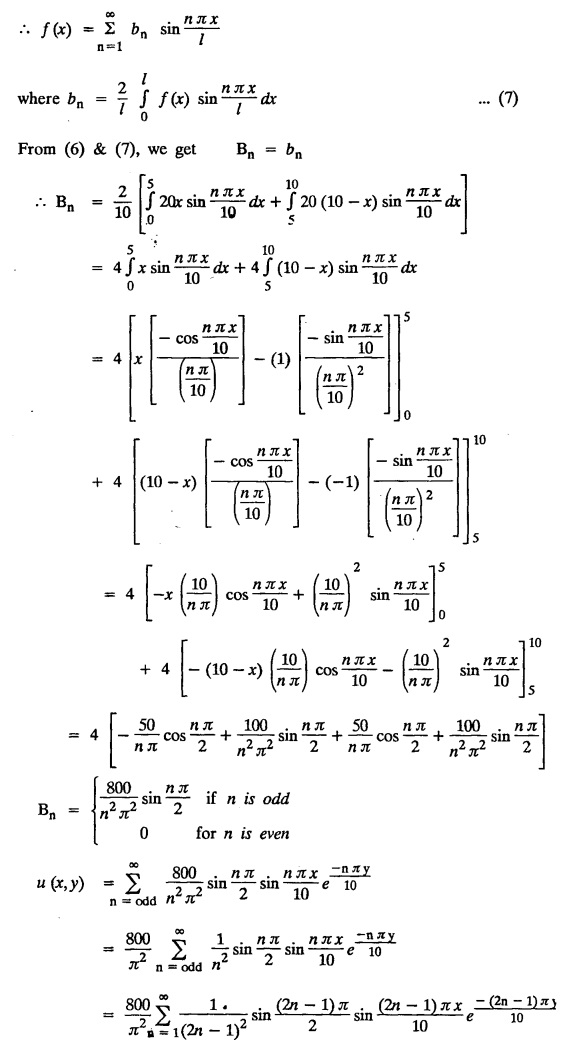
STEADY STATE SOLUTION OF TWO DIMENSIONAL EQUATION OF HEAT CONDUCTION (EXCLUDING INSULATED EDGES) TWO DIMENSIONAL HEAT FLOW EQUATIONS When the heat flow is along curves, instead of straight lines, the curves lying in parallel planes, the flow is called two dimensional. The differential equation for two dimensional heat flow for the unsteady case is Here u(x,y) is the temperature at any point (x, y) in time t, α2 is the diffusivity of the material. Let us consider now the flow of heat in a metal-plate in the xoy plane. Let the plate be of uniform thickness h, density ρ, thermal conductivity k and the specific heat c. Since the flow is two dimensional, the temperature at any point of the plate is independent of the z co-ordinate. The heat-flow lies in the xoy plane and is zero along the direction normal to the xoy plane. Now, consider a rectangular area PQRS of the plate with sides δx and δy, the edges being parallel to the co-ordinate axes, as shown in the figure. Then the quantity of heat entering the area PQRS per sec. through the surface Similarly, the quantity of heat entering the elt PQRS per sec through the surface The amount of heat which flows out through the surfaces QR and RS are Therefore, the total gain of heat by the rectangular element PQRS per sec. = in flow - out flow The rate of gain of heat by the area PQRS is also given by Equating the two-expressions for gain of heat per sec from (1) and (2), we have The equation (3) gives the temperature distribution of the plate in the transient state. In the steady-state, u is independent of t, so that i.e., v2u = 0, which is known as Laplace's equation in two-dimensions. Note: If the stream lines are parallel to the x axis, then the rate of change FOURIER SERIES SOLUTIONS IN CARTESIAN CO-ORDINATES Solution of the Laplace equation in two dimensions Here u is a function of x and y. So assume the solution where X is a function of x alone and Y is a function of y alone L.H.S. is a function of X alone and R.H.S. is a function of Y alone. Since X and Y are independent, each quantity is equal to a constant. Case (i) Let k be positive say k = p2, then (3) & (4) become Solving we get Case (3) Let k = 0 Thus the possible solutions of (1) are • Write the different solutions of Laplace's equation in cartesian coordinates. Solution: Problem 1. Obtain one dimensional heat flow equation from two dimensional heat flow equation for the unsteady case. Solution: The two dimensional unsteady state heat flow equation is when the stream lines are all parallel to the x axis, the rate of change So equation (1) is reduced to Problem 2. What is the equation to heat flow when the stream lines are non planar curves ? Solution: When the stream lines are non planar curves, the flow will be three dimensional and the heat equation will be Problem 3. What is the steady state heat equation in two dimensions in cartesian form ? Solution: The required equation is [Laplace equation] Problem 4. Write down Laplace's equation in cartesian co-ordinates. Solution : Problem 5. Write the three dimensional Laplace equation in cartesian form. Solution : Note: The two dimensional heat flow equation, when steady state conditions exist is uxx + uyy = 0. Type 1. Finite plate with value given in x direction : Boundary conditions : The suitable solution is given by Problems based on Finite Plates - Type 1 Example 3.5a(1): A square plate is bounded by the lines x = 0, y=0, x = l, y = l. Its faces are insulated. The temperature along the upper horizontal edge is given by u(x, l) = x(l - x) while the other three edges are kept at 0° C. Find the steady state temperature in the plate. Solution : The equation to be solved is From the given problem, we get the following boundary conditions: Now, the suitable solution which satisfies our boundary conditions is given by Apply condition (i) in equation (1), we get Apply condition (ii) in equation (2), we get Apply condition (iii) in equation (3), we get The most general solution is Now we apply condition (iv) in equation (5), we get To find Bn expand f(x) in a Fourier half range sine series From (6) and (7), we get Bn = bn = 0 if n is even. Substitute the value of An in equation (5), we get Example 3.5a(2): Find the steady state temperature distribution in a rectangular plate of sides a and b insulated at the lateral surface and satisfying the boundary conditions Solution: Applying condition (i) in equation (1), we get Applying condition (ii) in equation (2), we get Applying condition (iii) in equation (3), we get Substitute the value of D in equation (3), we get The most general form is Apply condition (iv), we get To find Вn expand ƒ (x) in a Fourier half range sine series Example 3.5a(3) The boundary value problem governing the steady state temperature distribution in a flat, thin, square plate is given by Find the steady-state temperature distribution in the plate. Sol. The equation to be solved is Given boundary conditions are (i) u (0, y) = 0, 0 < y < a The suitable solution is Apply condition (i) in equation (1), we get Apply condition (ii) in equation (2), we get If we take B = 0 and already A = 0 then we get a trivial solution, Therefore, B ≠ 0 ⸫ sin p a = 0 Apply condition (iii) in equation (3), we get Apply condition (iv) in equation (5), we get Equating the like terms, we get Type 2. Finite plate with value given in y direction : The most general solution is Apply condition (iv), we get Problems based on Finite Plates - Type 2 Example 3.5a(4): A square plate is bounded by the lines x = 0, x=a, y = 0, y = a, of a square plane bounded by the lines x = 0, y = 0, y = a are kept at temperature 0° C. The side x = a is kept at temperature given by u (a, y) = 100, 0 < y < a. Solution: The equation to be solved is Applying condition (i) in equation (1), we get Applying condition (ii) in equation (2), we get Applying condition (iii) in equation (3), we get The most general solution is Applying condition (iv) in equation (5), we get To find Вn expand 100 in a Fourier half range sine series Example 3.5a(5): A square plate is bounded by the lines x = 0, x=a, y = 0, y = a of a square plane bounded by the lines x = a, y = 0, y = a are kept at temperature 0° C. The side x = 0 is kept at temperature given by u (0, y) = 100, 0 < y < a. Find u (x, y). Solution : The equation to be solved is Applying conditions (iii) in equation (3), we get The most general solution is Applying condition (iv) in equation (5), we get To get Bn expand 100 in a Fourier half range sine series Substitute An is equation (5), we get Problems based on Finite Plates : Type 3. (Combination of Type 1 & Type 2) Example 3.5a(6) : A rectangular plate is bounded by the lines_x = y = 0, x = a and y = b. It's surfaces are insulated and the temperature along two adjacent edges are kept at 100° C, while the temperature along the other two edges are at 0° C. Find the steady state temperature at any point in the plate. Also find the steady state temperature at any point of a square plate of side 'a' if two adjacent edges are kept at 100° C and the others at 0° C. Solution: Let u (x, y) be the temperature satisfying the equation Then the boundary conditions are given by Now, we split the solutions into two solutions. i.e., u (x, y) = u1 (x, y) + u2 (x, y) where u1 (x, y) and u2 (x, y) are solutions of (1) and further u1 (x, y) is the temperature at any point P with the edge BC maintained at 100° C and the other three edges at 0° C where u2 (x, y)is the temperature at P with the edge AB maintained at 100° C and the other three edges at 0° C. Therefore, the boundary conditions for the functions u1 (x, y) and u2 (x, y) are as follows. Clearly, both u1 and u2 satisfy the equation (1). Solving (1) aud choosing the suitable solution we have, By applying the condition (v) on (2), we get By applying the condition (vii) on (3), we get By applying the condition (vi) on (4), we get The most general solution is By the condition (viii), we get which is a half range sine series for f(x) = 100 defined in (0, a) Similarly, 3.5(b). Infinite Plates PROBLEMS ON INFINITE PLATES Example 3.56(1): A rectangular plate with insulated surface is 10 cm wide, so long compared to its width that it may be considered infinite in length. If the temperature at the short edge y = 0 is given by u = x for 0 ≤ x ≤ 5 and 10 x for 5 < x < 10 and the two long edges x = 0, x = 10 as well as the other short edge are kept at 0° C. Find the temperature function u (x, y) at any point of the plate. Solution: The equation to be solved is From the given problem, we get the following boundary conditions. Applying condition (i) in equation (1), we get Applying condition (ii) in equation (2), we get Applying condition (iii) in equation (3), we get Substitute, C = 0 in equation (3), we get The most general solution is Now, applying condition (iv) in equation (5), we get To find Bn then we expand f(x) as a Fourier half range sine series in (0, 10) Substitute, the value of Bn in equation (5), we get Example 3.56(2): A rectangular plate with insulated surface is 10 cm wide and so long compared to its width that it may be considered infinite in length without introducing an appreciable error. If the temperature of the short edge y = 0 is given by Proof : Let u (x, y) be the temperature at any point (x,y) in the steady state. Then u satisfies the differential equation V2 u = 0 From the given problem, we get the following boundary conditions Now, the suitable solution which satisfies our boundary conditions is given by The most general solution is Apply condition (iv) in equation (5), we get To find Bn then we expand f(x) as a Fourier half-range sine series in [0, 10] Example 3.5b(3) : A rectangular plate with insulated surfaces is 10 cm wide and so long compared to its width that it may be considered infinite in length without introducing an appreciable error. If the temperature along are short edge y = 0 is u(x, 0) = 4 (10x − x2) for 0 < x < 10 while the two long edges as well as the other short edge are kept at 0° C, find the steady state temperature function u(x, y). Solution: Let u(x,y) be the temperature at any point (x, y) in the steady state. Then u satisfies the differential equation Apply condition (iv) in equation (5), we get To find Bn then we expand f(x) as a Fourier half range sine series in (0, 10) Substituting the value of Bn in equation (5), we get Horizontal plate Example 3.5b(4) : An infinitely long rectangular plate with insulated surface is 10 cm wide. The two long edges and one short edge are kept at zero temperature, while the other short edge x = 0 is kept at temperature given by u (0, y) = Find the steady state temperature distribution in the plate. Solution: The equation to be solved is From the given problem, we get the following boundary conditions Now, the suitable solution which satisfies our boundary conditions is given by Applying condition (i) in equation (1), we get Applying condition (ii) in equation (2), we get Applying condition (iii) in equation (3), we get The most general solution is Applying condition (iv) in equation (5), we get To find Bn, expand ƒ (y) in a half range Fourier sine series in [0,10]. = 0 if n is even. Substitute, Bn in equation (5), we get Example 3.5b(5) : A rectangular plate with insulated surface is 8 cm wide and so long compared to its width that it may be considered infinite in length without introducing an appreciable error. If the temperature along the short edge y = 0 is given by u (x, 0) = 100 sin Solution: The equation to be solved is Now, the suitable solution which satisfies our boundary condition is given by Applying condition (i) in equation (1), we get Applying condition (ii) in equation (2), we get Substitute the value C = 0 in eqn. (3), we get The most general solution is Applying condition (iv) in equation (5), we get 1. A square plate is bounded by the lines x = 0, y = 0, x = 20, y = 20. Its faces are insulated. The temperature along the upper horizontal edge is given by u(x, 20) = x (20 - x) when 0 < x < 20 while the other three edges are kept at 0° C. Find the steady state temperature in the plate. 2. A square plate has its faces and the edge y=0 insulated. Its edges x = 0 and x = л are kept at 0° C and the edge у=л is kept at temperature f(x). Find the steady state temperature. 3. Find the steady state temperature at any point of a square plate whose two adjacent sides are kept at 0° C and the other two edges are kept at 100° C. 4. A rectangular metal plate is bounded by the lines x = 0, x = a, y = 0 and y = b. The three sides x = 0, x = a and y = b are insulated and the side y = 0 is kept at temperature 5. The three sides x 0, x = a, y = 0 of a square plate bounded by the lines x 0, x = a, y = 0 and y = a are kept at temperature 0° C. The side y = a is kept at steady temperature given by u (x, a) = bx (x − a), 0 ≤ x ≤ a when b is a constant. Find the steady-state temperature u (x, y) in the plate. 6. Find the solution of the equation V2v = 0 for 0 < x <л, 0 < y <л, given u (0,y) = u(л,у) = u(x, π) 0 u (x, 0) = sin2x. 7. A rectangular plate is bounded by the lines x = 0, x = a, y = 0 and y = b and the temperature at the edges are given by Find the steady state temperature distribution inside the plate. 8. A long rectangular plate has its surface insulated and the two long sides as well as of the short sides are maintained at 0° C. Find an expression for the steady state temperature u (x, y) if the short side y=0 is л cm long and is kept at u°0 C. 9. An infinitely long rectangular plate with insulated surface is 10 cm wide. The two long edges and one short edge are kept at 0° C temperature while the other short edge x = 0 is kept at temperature is given by Find the steady state temperature distribution in the plate. 10. A long rectangular. plate has its surfaces insulated and the two long sides as well as one of the short sides are kept at 0° C. While the other sides u (x, 0) = 3x and the length being 5 cm. Find u (x,y). 11. A long rectangular plate of width l cm with insulated surface has its temperature u equal to zero on both long sides one of the shorter sides so that u (0, y) = u (l, y) = u(x, ∞) = 0 and u (x, 0) = kx. Find u (x, y). 12. An infinitely long vertical uniform plate is bounded by two parallel edges and an end at right angles to them. The breadth is л. This end is maintained at a temperature uo at all points and other edges are kept at zero temperature. Determine the temperature at any point of the plate in the steady state. 13. An infinite long plate of width л with insulated surfaces has its temperature zero on both long sides and are of the short sides. The side y = 0 is maintained at a temperature 3x. Find the steady state temperature u (x, y). 14. A rectangular plate with insulated surface is 10 cm wide so long compared to its width that it may be considered infinite length. If the temperature along short edge y = 0 is given u (x, 0) = 8 πx/10 sin when 0 < x < 10, while the two long edges x = 0 and x = 10 as well as the other short edge are kept at 0°C, find the steady state temperature function u (x, y). ANSWERS 3.5Introduction


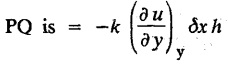

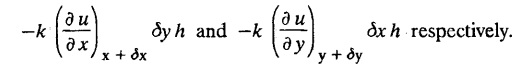
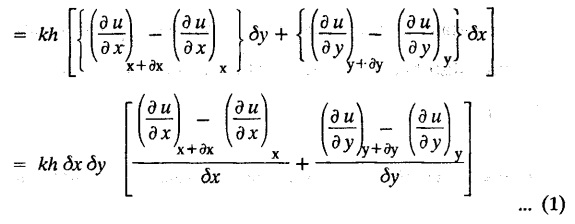
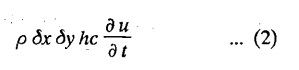

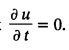 Hence the temperature distribution of the plate in the steady-state is
Hence the temperature distribution of the plate in the steady-state is 
![]() of the temperature in the direction of the y-axis will be zero. Then the heat-flow equation is reduced to
of the temperature in the direction of the y-axis will be zero. Then the heat-flow equation is reduced to 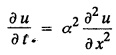 which is the heat-flow equation in one-dimension.
which is the heat-flow equation in one-dimension.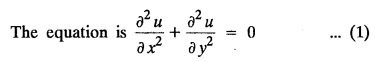

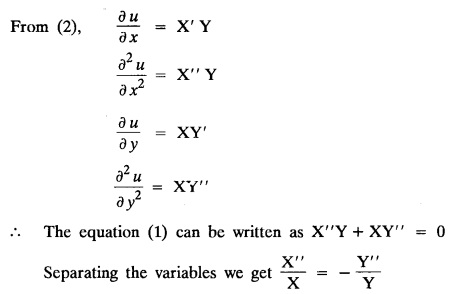



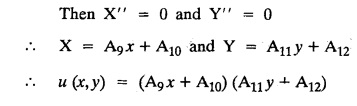

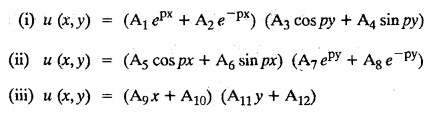
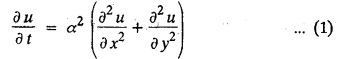
![]() of temperature in the y direction will be zero.
of temperature in the y direction will be zero.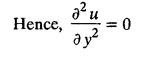
 which is the p.d.e. of one dimensional heat flow.
which is the p.d.e. of one dimensional heat flow.



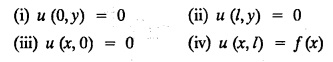

3.5a. Finite Plates
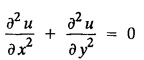


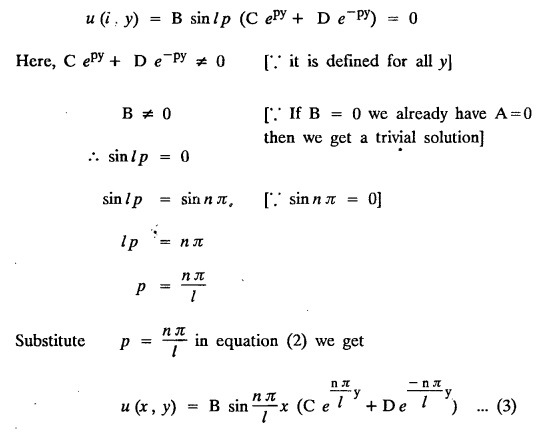

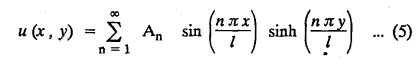
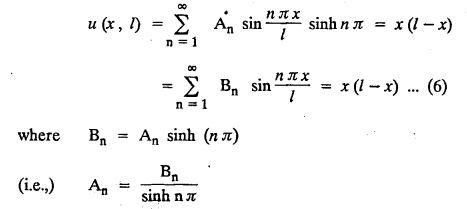
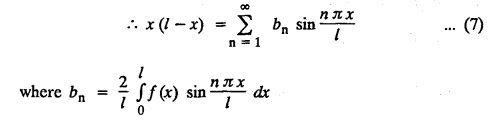






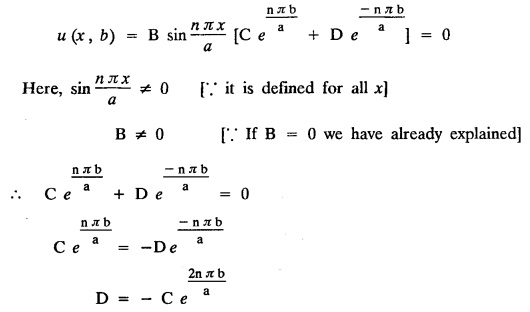
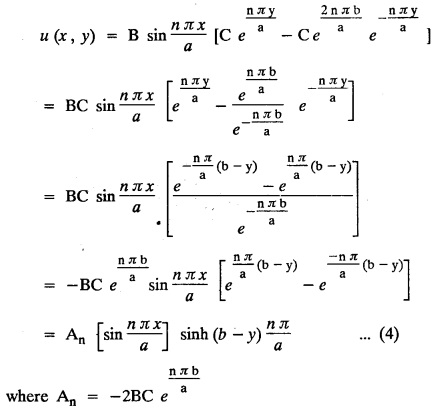
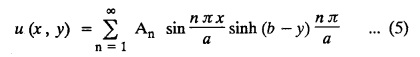



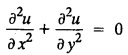

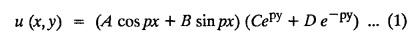

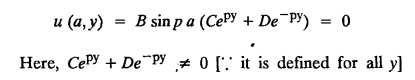

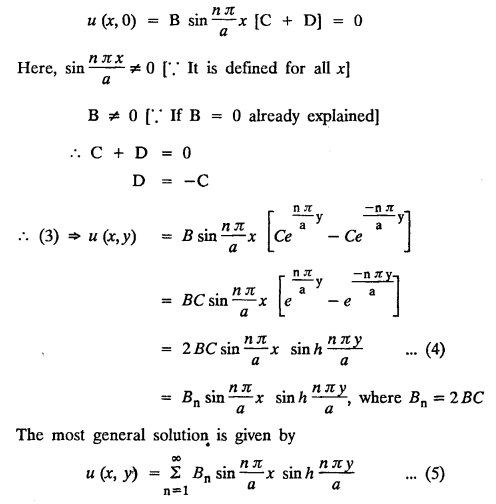

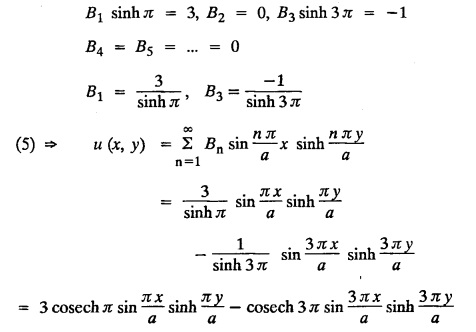

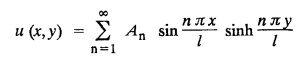
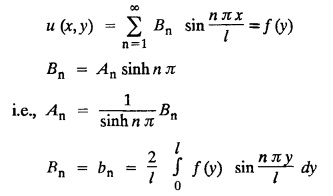




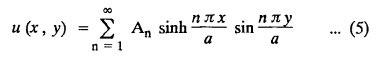




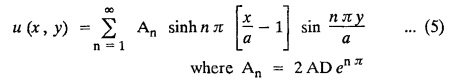




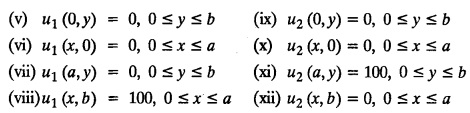
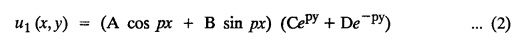






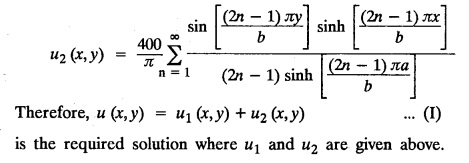
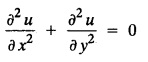



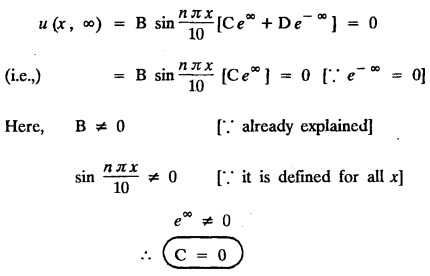
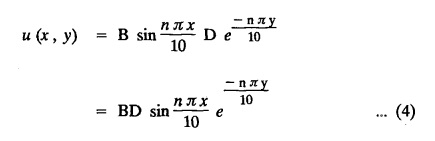

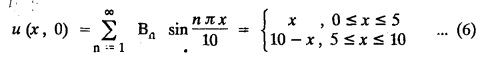


 and the two long edges x = 0 and x = 10 as well as the other short edge are at 0° C. Prove that the temperature, u (x, y) at any point (x, y) of the plate is given by
and the two long edges x = 0 and x = 10 as well as the other short edge are at 0° C. Prove that the temperature, u (x, y) at any point (x, y) of the plate is given by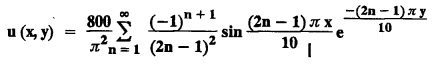
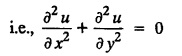
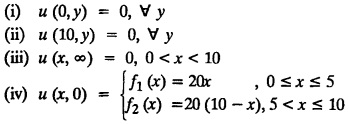
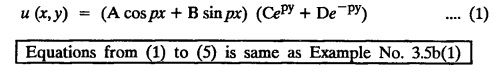



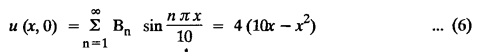

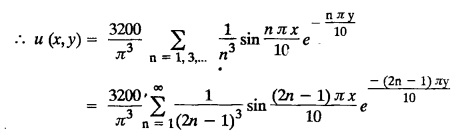

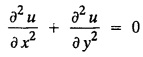




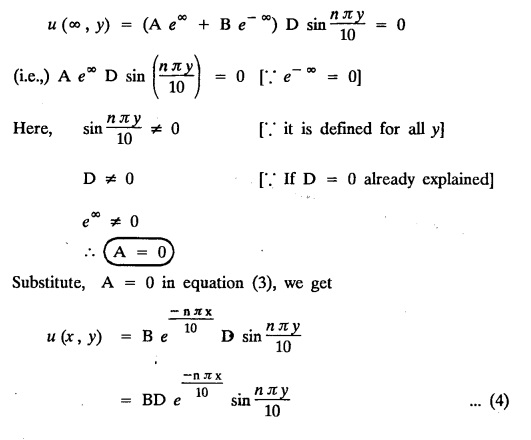
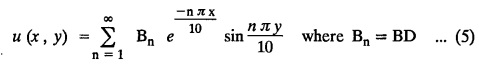
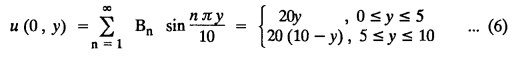


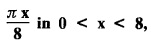 while the long two edges x=0 and x = 8 as well as the other short edge are kept at 0° C, find the steady state temperature function u(x, y).
while the long two edges x=0 and x = 8 as well as the other short edge are kept at 0° C, find the steady state temperature function u(x, y).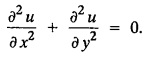

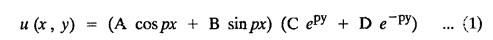

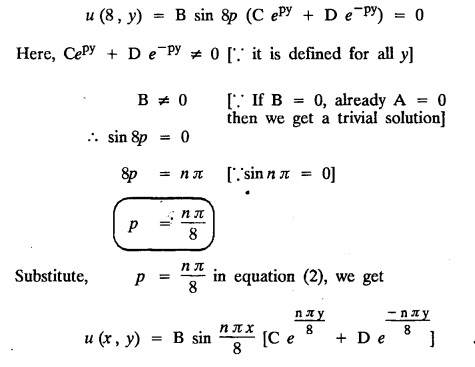
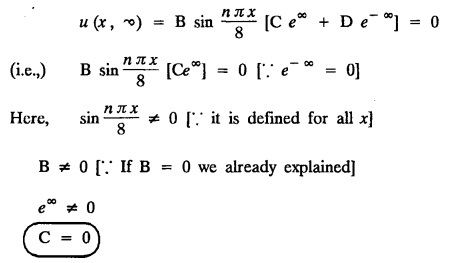



EXERCISE 3.5![]() Show that the temperature in the steady state is
Show that the temperature in the steady state is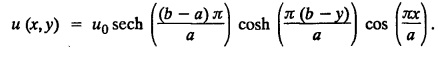
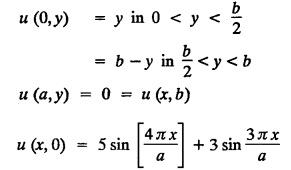
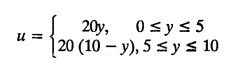

Transforms and Partial Differential Equations: Unit III: Applications of Partial Differential Equations : Tag: : Solved Example Problems - Steady state solution of two dimensional equation of heat conduction (Heat flow equations) (excluding insulated edges)
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
