Engineering Physics: Unit III: a. Oscillations
Stationary waves or Standing waves
Analytical method, Definition, Equation, Characteristics
When two progressive waves of same amplitude and wavelength travelling along a straight line in opposite directions superimpose on each other, stationary waves are formed.
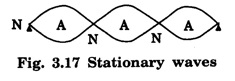
STATIONARY WAVES OR STANDING WAVES When two progressive waves of same amplitude and wavelength travelling along a straight line in opposite directions superimpose on each other, stationary waves are formed. Let us consider a progressive wave of amplitude a and wavelength λ travelling in the direction of X axis. This wave is reflected from a free end and it travels in the negative direction of X axis, then According to principle of superposition, the resultant displacement is y = y1 + y2 This is the equation of a stationary wave. (i). A points where ⸫ A = ±2a. At these points of the resultant amplitude is maximum. They are called antinodes (Fig. 3.17). (ii) At points where ⸫ A = 0. The resultant amplitude is zero at these points. They are called nodes (Fig. 3.17). The distance between any two successive antinodes or nodes is equal to (iii) When (iv) When 1. The waveform remains stationary. 2. Nodes and antinodes are formed alternately. 3. The points where displacement is zero are called nodes and the points where the displacement is maximum are called antinodes. 4. Pressure changes are maximum at nodes and minimum at antinodes. 5. All the particles except those at the nodes, execute simple harmonic motions of same period. 6. Amplitude of each particle is not the same, it is maximum at antinodes and decreases gradually and is zero at the nodes. 7. The velocity of the particles at the nodes is zero. It increases gradually and is maximum at the antinodes. 8. Distance between any two consecutive nodes or antinodes is equal to λ/2, whereas the distance between a node and its adjacent antinode is equal to λ/4. 9. There is no transfer of energy. All the particles of the medium pass through their mean position simultaneously twice during each vibration. 10. Particles in the same segment vibrate in the same phase and between the neighbouring segments, the particles vibrate in opposite phase. In musical instruments like sitar, violin, etc. sound is produced due to the vibrations of the stretched strings. When a string under tension is set into vibration, a transverse progressive wave moves towards the end of the wire and gets reflected. Thus stationary waves are formed.Analytical method



 the values of
the values of
 the values of
the values of 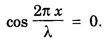
![]() and the distance between an antinode and a. node is
and the distance between an antinode and a. node is ![]()
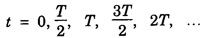 then
then  the displacement is zero.
the displacement is zero.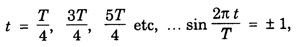 the displacement is maximum.
the displacement is maximum.Characteristics of stationary waves
Standing waves in strings
Differences between Progressive waves and Stationary waves

Engineering Physics: Unit III: a. Oscillations : Tag: : Analytical method, Definition, Equation, Characteristics - Stationary waves or Standing waves
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
