Theory of Machines: Unit IV: Force Analysis
static equilibrium of various members
Force Analysis - Theory of Machines
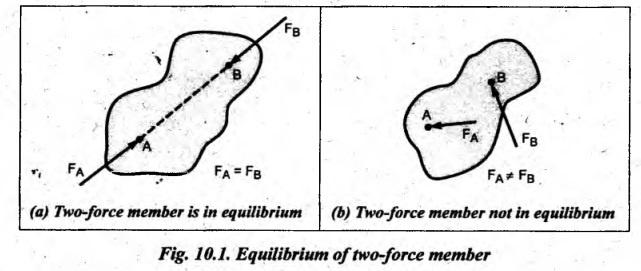
Fig.10.1(a) shows the free body diagram of a two-force member, which is in equilibrium.
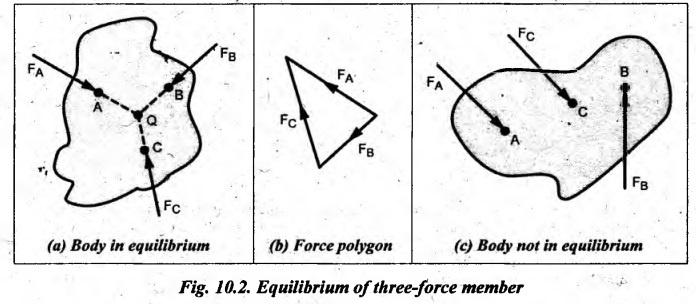
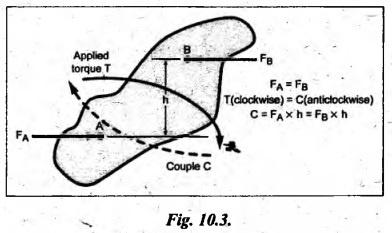
STATIC EQUILIBRIUM OF VARIOUS MEMBERS • Fig.10.1(a) shows the free body diagram of a two-force member, which is in equilibrium. From the equations of equilibrium, (i) ΣF = FA + FB = 0 This requires that FA and FB have equal magnitudes and opposite directions. (ii) E M = 0 This is possible only when FA and FB must have the same line of action (otherwise the sum of moments not equal to zero). Thus a member under the action of two forces will be in equilibrium, only when (1) The forces are of the same magnitude, (ii) The forces act along the same line, and (iii) The forces are in opposite directions. • Fig.10.1(b) shows a two-force member not in equilibrium, because it does not satisfy the above-said conditions. • A body or member will be in equilibrium under the action of three forces, only when (i) The resultant of the forces is zero (i.e., force polygon should close), and (ii) The lines of action of the forces intersect at a point (which is known as point of concurrency). Illustration Let us consider the three-force member as shown in Fig.10.2(a). Let the lines of action of three forces FA, FB and FC intersect at point O, which is known as the point of concurrency. The resultant of these forces is zero. This is verified by adding the forces vectorially, which gives a closed force polygon as shown in Fig.10.2(b). So far Σ F= 0, force equilibrium equation only satisfied. To satisfy the moment equilibrium, i.e., & M = 0, the lines of action of all three forces must intersect at the common point O. That is, the three forces acting on the body must be concurrent. Fig.10.2(c) shows a three-force member not in equilibrium, because it does not satisfy the above-said conditions. • Fig.10.3 shows a member acted upon by two equal forces F1 and F2 and an applied torque T. • A member under the action of two forces, and an applied torque will be in equilibrium, only when (i) The forces are equal in magnitude, parallel in direction and opposite in sense, and (ii) The forces form a couple C, which is equal and opposite to the applied torque. In the above expression, the applied torque T is clockwise whereas the couple formed by FA and FB (shown in dotted line in Fig.10.3) is anticlockwise.1. Equilibrium of a Two-Force Member
2. Equilibrium of a Three-Force Member
3. Equilibrium of a Member with Two Forces and a Torque
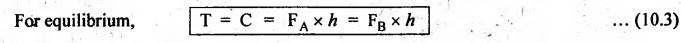
Theory of Machines: Unit IV: Force Analysis : Tag: : Force Analysis - Theory of Machines - static equilibrium of various members
Related Topics
Related Subjects
Theory of Machines
ME3491 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
