Transforms and Partial Differential Equations: Unit IV: Fourier Transforms
Statement of Fourier Integral Theorem
Sine and Cosine | Solved Example Problems
Integral transforms are used in the solution of partial differential equations.
Unit-IV FOURIER TRANSFORMS Statement of Fourier integral theorem - Fourier transform pair Fourier sine and cosine transforms - Properties - Transforms of simple functions - Convolution theorem - Parseval's identity. Integral transforms are used in the solution of partial differential equations. The choice of a particular transform to be used for the solution of a differential equation depends upon the nature of the boundary conditions of the equation and the facility with which the transform F(s) can be converted to give f(x). 4.1.a Fourier integral theorem (without proof) If f(x) is piece-wise continuously differentiable and absolutely integrable in (-∞, ∞), then Equation (1) can be re-written as This is known as Fourier integral theorem or Fourier integral formula. (OR) Let us assume the following conditions on a function f (x) 1. f (x) is piece-wise continuous in any finite interval (a, b) 2. Then the Fourier integral theorem states that The double integral in the right hand side is known as a Fourier integral expansion of f (x) (OR) If f (x) is a function defined in (-l, l) satisfying Dirichlet's conditions, then The double integral in the right hand side is known as Fourier integral to represent ƒ (x) Note: We assume the following conditions on f(x) (i) f(x) is defined as single-valued except at finite points in (-l, l) (ii) f(x) is periodic outside (-l, l) with period 2l. (iii) f(x) and f'(x) are sectionally continuous in (-l, l) (iv) i.e., f(x) is absolutely integrable in (-∞, ∞) I.(a) Problems based on Fourier integral theorem : Example 4.1.a(1): Show that f(x) = 1, 0 < x < ∞ cannot be represented by a Fourier integral. Solution : Hence, f (x) = 1 cannot be represented by a Fourier integral. Example 4.1.a(2) : Solution: We know that, the Fourier integral formula for ƒ (x) is Aliter : We know that, the Fourier integral formula for f (x) is Example 4.1.a(3) : Express the function Solution: We know that, the Fourier integral formula for ƒ (x) is Example 4.1.a(4) Find the Fourier integral of the function Solution: We know that, the Fourie integral formula for f(x) is Example 4.1.a(5) Find the Fourier integral of the function Solution: We know that, the Fourier integral formula for f(x) is Verification : Put x = 0 in (4), we get Hence, verified. 4.1.b Complex form of the Fourier integrals. The Fourier integral formula for f(x) is because cos [λ (t − x)] is an even function of λ. Also since sin [λ (t − x)] is an odd function of λ. which is the complex form of the Fourier integral. Fourier sine and cosine integrals Proof: We know that, the Fourier integral theorem is Note I : Equation (2) can be re-written as Note II : Equation (3) can be re-written as I.(b) Problems based on Fourier cosine and Fourier sine integrals Example 4.1.b(1) : Find Fourier cosine integral of the function e-ax. Hence deduce the value of the integral Solution: We know that, the Fourier Cosine integral of ƒ (x) is given by Example 4.1.b(2): Using Fourier integral formula, show that Solution: We know that, the Fourier Cosine integral of f (x) is given by Here, f (x) = e-x cos x Example 4.1.b(3) Express f(x) : Solution : We know that, the Fourier sine integral of ƒ (x) is given by Note: If x = π is a finite point of discontinuity of f(x), then Example 4.1.b(4): Using the Fourier integral representation show that Solution : We know that, the Fourier sine integral of ƒ (x) is given by Example 4.1.b(5) Using Fourier integral formula, prove that Solution: We know that, the Fourier sine integral of ƒ (x) is given by Example 4.1.b(6): Applying the Fourier sine integral formula to the function Solution: We know that, the Fourier sine integral of ƒ (x) is given byINTRODUCTION
1. STATEMENT OF FOURIER INTEGRAL THEOREM
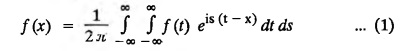

 is convergent.
is convergent.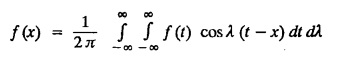

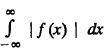 converges
converges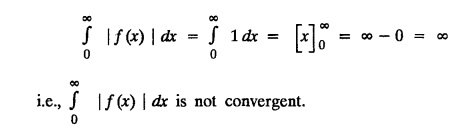




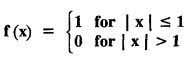 as a Fourier integral. Hence evaluate
as a Fourier integral. Hence evaluate 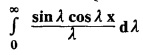 and find the value of
and find the value of 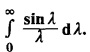

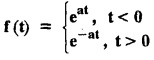
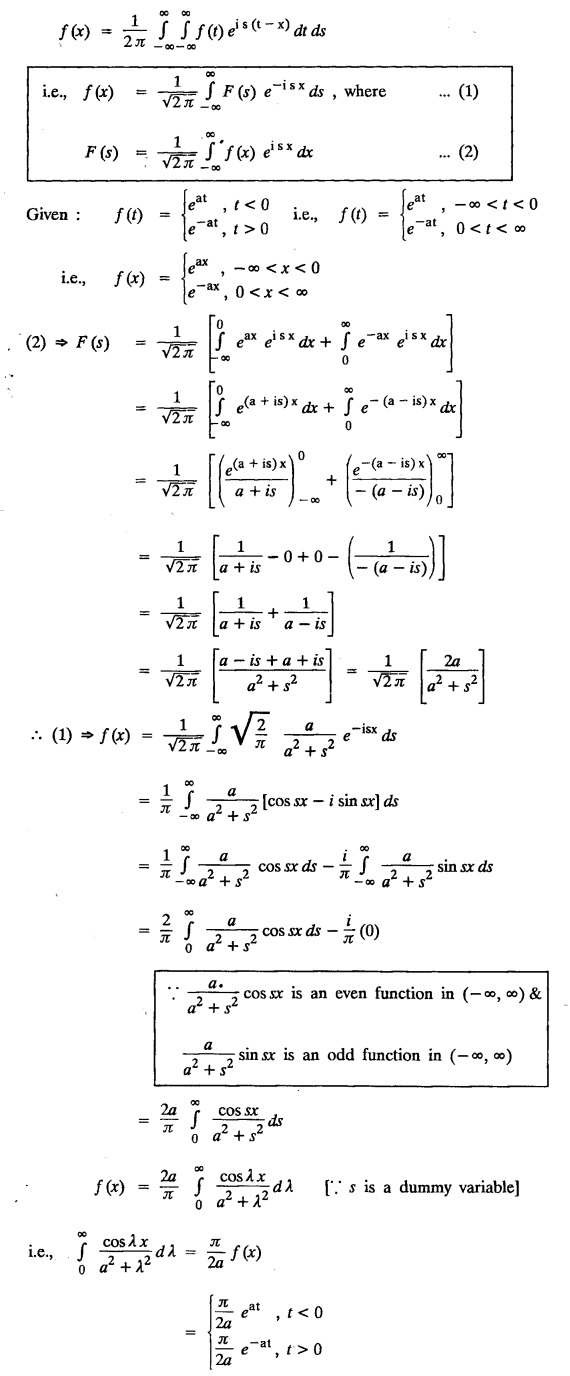
 Verify the representation directly at the point x = 0.
Verify the representation directly at the point x = 0.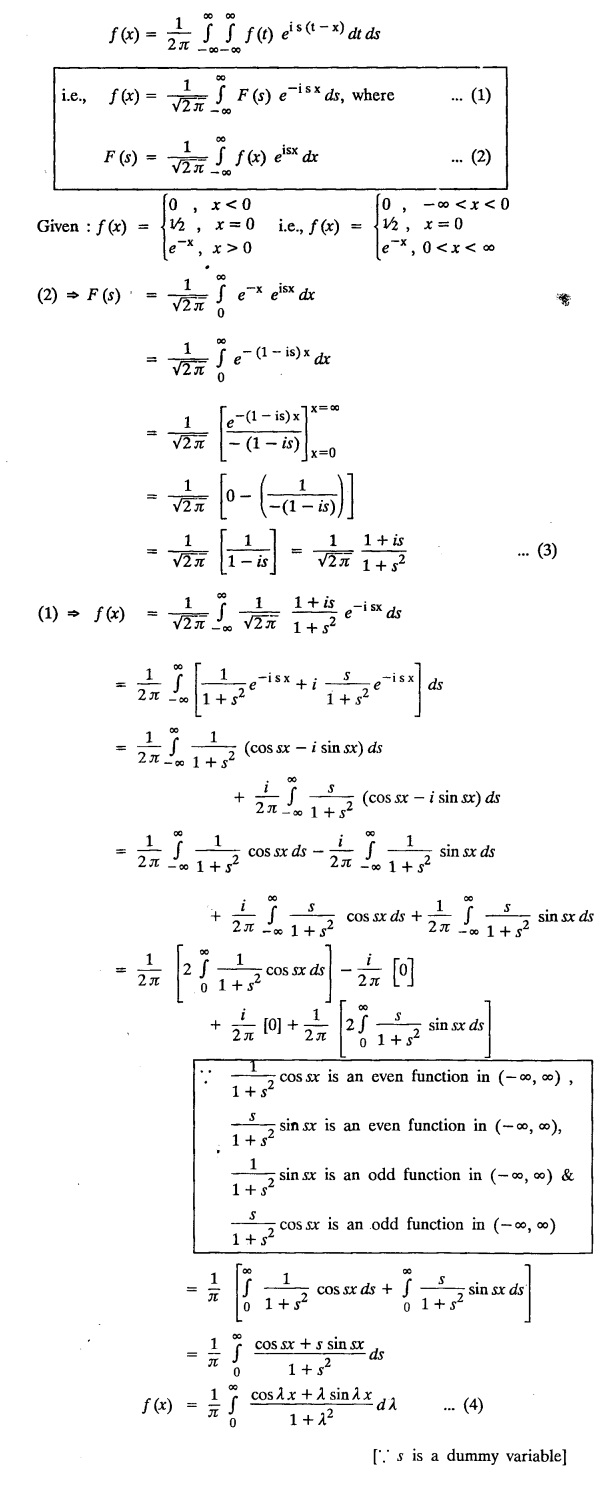



FOURIER SINE AND COSINE INTEGRALS


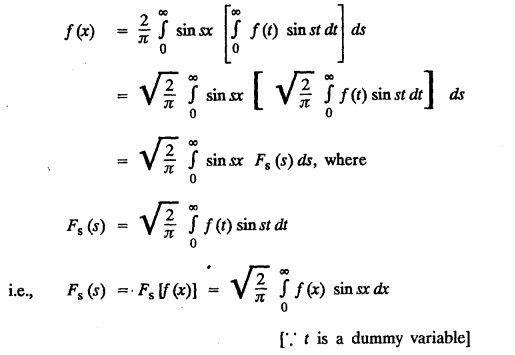
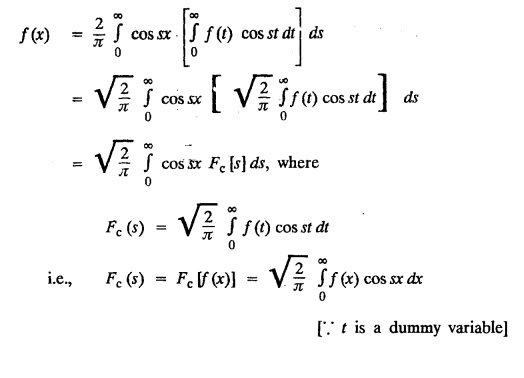
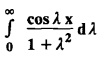




 as a Fourier sine integral and hence evaluate
as a Fourier sine integral and hence evaluate 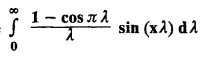






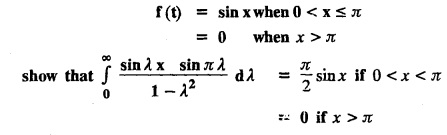

Transforms and Partial Differential Equations: Unit IV: Fourier Transforms : Tag: : Sine and Cosine | Solved Example Problems - Statement of Fourier Integral Theorem
Related Topics
Related Subjects
Transforms and Partial Differential Equations
MA3351 3rd semester civil, Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
