Hydraulics and Pneumatics: Unit IV: Pneumatic and Electro Pneumatic Systems
some numerical examples illustrating perfect gas laws
Pneumatic and Electro Pneumatic Systems - Hydraulics and Pneumatics
some numerical examples illustrating perfect gas laws: Pneumatic and Electro Pneumatic Systems - Hydraulics and Pneumatics
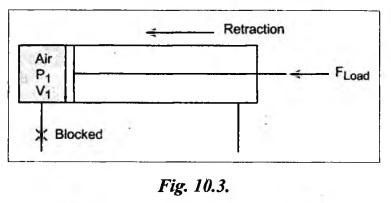
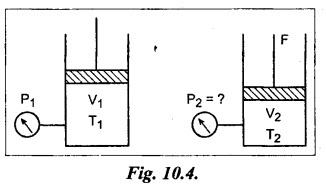
SOME NUMERICAL EXAMPLES ILLUSTRATING PERFECT GAS LAWS Example 10.1 A compressed air receiver has a volume of 0.6 m3 at 4 bar gauge pressure. If the volume of the same receiver is increased to 1 m3, determine the gauge pressure of the air assuming a constant temperature process. Given Data: V1 = 0.6 m3; P, (gauge) = 4 bar; V2 = 1 m3; T = Constant. Solution: Given that temperature remains constant, therefore applying Boyle's law, We get P1V1 = P2 V2 Here the P1 and P2 represents absolute pressures. Example 10.2 The 50 mm diameter piston of the pneumatic cylinder of Fig.10.3 retracts 150 mm from its present position (P1 = 2.5 bars gauge, V1 350 cm3) due to the external load on the rod. If the port at the blind end of the cylinders is blocked, find the new pressure, assuming the temperature does not change. Given Data: Dpiston = 50 mm; Stroke = L = 150 mm; P1 (gauge) = 2.5 bar; V1 = 350 cm3 = 350 × 10-6 m3; T = Constant. Solution: Now using the Boyle's law, we get Example 10.3 The cylinder of Fig.10.3 has an initial position where P1 = 2.5 bars gauge and V1 = 350 cm3, as controlled by the load on the rod. The air temperature is 35°C. The load on the rod is held constant to maintain constant air pressure, but the air temperature is increased to 70°C. Find the new volume of air at the blind end of the cylinder. Given Data: P1 (gauge) = 2.5 bar; V1 = 350 cm3 ; T1 = 35°C = 35 + 273 = 308 K; P = constant ; T2 = 70°C = 70 + 273 = 343 K Solution: Given that pressure is constant, so using the Charles' law, we get Example 10.4 The cylinder of Fig.10.3 has a locked position (V1 = constant). P1 = = 2.5 bars gauge and T1 = 30°C. If the temperature increases to 75°C, what is the new pressure in the blind end? Given Data: V1 = Constant; P1(gauge) = 2.5 bars or P1 (absolute) = 2.5 + 1 = 3.5 bars; T1 = 30°C = 30 + 273 = 303 K; T2 = 75°C = 75 + 273 = 348 K. Solution: Given that volume is constant, so applying the Gay-Lussac's law, we get Example 10.5 Gas at 75 bars gauge and 45°C is contained in the 1000 cm3 cylinder of Fig.10.4. A piston compresses the volume to 750 cm3 while the gas is heated to 110°C. What is the final pressure in the cylinder. Given Data: P1 (gauge) = 75 bars or P1 (absolute) = 75 + 176 bars; T1 = 45°C = 45 + 273 = 318 K; V1 = 1000 cm3 ; V2 = 750 cm3 ; T2 = 110°C = 110 + 273 = 383 K. Solution: We know the general gas law that,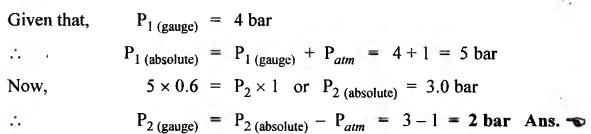
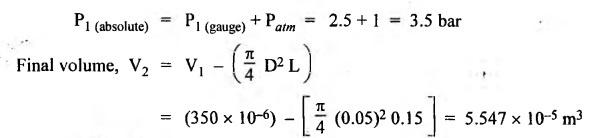
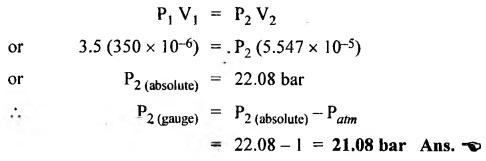
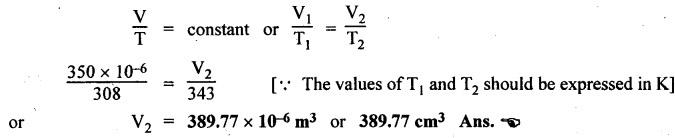
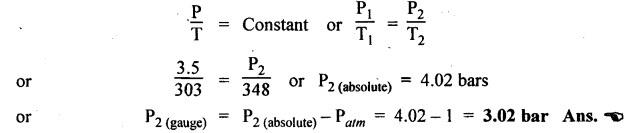

Hydraulics and Pneumatics: Unit IV: Pneumatic and Electro Pneumatic Systems : Tag: : Pneumatic and Electro Pneumatic Systems - Hydraulics and Pneumatics - some numerical examples illustrating perfect gas laws
Related Topics
Related Subjects
Hydraulics and Pneumatics
ME3492 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
