Hydraulics and Pneumatics: Unit I: Fluid Power Priniciples and Hydraulic Pumps
some illustrative example problems
Fluid Power Priniciples and Hydraulic Pumps - Hydraulics and Pneumatics
For better understanding of the basic principles of hydraulics discussed so far, some simple numerical problems have been presented below.
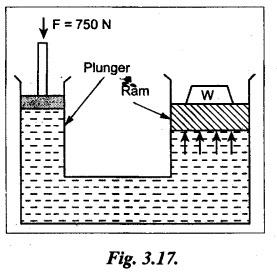
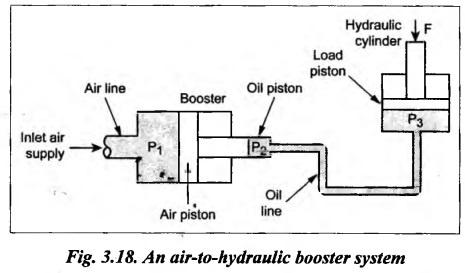
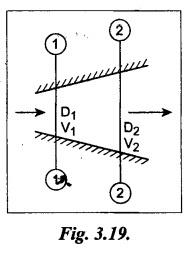
SOME ILLUSTRATIVE EXAMPLE PROBLEMS For better understanding of the basic principles of hydraulics discussed so far, some simple numerical problems have been presented below. Example 3.1 (a) Find the pressure at a depth of 10 m below the free surface of water in a reservoir. (b) Find the height of water column corresponding to a pressure of 70 kPa. (a) Given Data: h = 10 m. Solution: We know that, P = ρ g h = 1000 × 9.81 × 10 [⸪ ρwater = 1000 kg/m3] = 0.981 × 105 N/m2 = 0.981 bar Ans. (b) Given Data: P = 70 kPa = 70 × 103 N/m2. Solution: We know that, P = ρ g h or 70 × 103 = 1000 × 9.81 × h h = 7.135 m of water column Ans. On Atmospheric, Gauge, and Absolute Pressures Example 3.2. If a mercury barometer reads 700 mm and Bourdon gauge at a point in a flow system reads 500 kPa, what is the gauge, atmospheric, and absolute pressures at the point. Take specific gravity of mercury = 13.6. Solution: (i) Gauge pressure: We know that the gauge pressure is the pressure measured with the help of pressure measuring instrument - Bourdon gauge. Therefore the gauge pressure = 500 kPa or 5 bar Ans. (ii) Atmospheric pressure : Barometer reading (atmospheric pressure) = 700 mm of mercury or h = 700 × 13.6 mm of water ⸫ Atmospheric pressure, P = ρ g h = 1000 × 9.81 x 9.52 = 93.39 kN/m2 Ans. (iii) Absolute pressure: We know that, Absolute pressure = Gauge pressure + Atmospheric pressure = 500 + 93.39 = 593.39 kN/m2 Ans. Example 3.3 Convert - 3.5 kPa pressure to an absolute pressure in kPa. Given Data : Pgauge = - 3.5 kPa Solution: Absolute pressure = Gauge pressure + Atmosphere pressure = -3.5 + 101.3 = 97.8 kPa Ans. On Work and Power Example 3.4 A person applied 200 N force to move a load 2.5 m in 90 s. (a) How much work is done? (b) What is the power exerted by the person? Given Data: F = 200 N ; d = 2.5 m; t = 90 s. Solution: On Application of Pascal's Law Example 3.5 The diameters of plunger and ram of an hydraulic press (shown in Fig.3.17) are 50 mm and 125 mm respectively. Find the weight lifted by the hydraulic press when the force applied at the plunger is 750 N. Given Data: D1 = 50 mm; D2 = 125 mm ; F1 = 750 N. Solution: Example 3.6 For the pressure booster of Fig.3.18, the following data are given : Inlet oil pressure (P1) = 0.85 MPa ; Air piston area (A1) = 0.025 m2 ; Oil piston area (A2) = 0.0015 m2; Load piston area (A3) = 0.015 m2. Determine the load-carrying capacity F of the system. Given Data : P1 = 0.85 MPa = 0.85 × 106 N/m2; A1 = 0.025 m2; A2 = 0.0015 m2; A3 = 0.015 m2. Solution: Refer Fig.3.18. Let us first find the booster discharge pressure P2. We know that, Booster input force = Booster output force Example 3.7 The kinematic viscosity of a hydraulic oil is 0.9 stroke. If it is flowing in a 35 mm diameter pipe at a velocity of 4 m/s, what is the Reynolds number? Is the flow laminar or turbulent? Given Data: v = 0.9 stroke = 0.9 cm2/s = 0.9 × 10-4 m2/s; D = 35 mm; V = 4 m/s. Solution: We know that, Example 3.8 A hydraulic pump delivers fluid at 50 Lpm (i.e., litres per minute) through a 30 mm diameter pipe. Determine the fluid velocity. Given Data: Solution: Example 3.9 The diameters of a pipe at the sections 1-1 and 2-2 are 100 mm and 150 mm respectively. If the velocity of water flowing through the pipe at section 1–1 is 3.5 m/s, find : (a) • Discharge through the pipe, and (b) Velocity of water at section 2–2. Given Data: D1 = 100 mm; D2 = 150 mm; V1 = 3.5 m/s. Solution: Refer Fig.3.19. (a) Discharge through the pipe (Q) : (b) Velocity of water at section 2–2 (v 2) : Using the continuity equation, we get Example 3.10 Oil with specific gravity 0.9 enters a tee, as shown in Fig.3.20, with velocity v1 = 5 m/s. The diameter at section 1 is 10 cm, the diameter at section 2 is 7 cm v1 and the diameter at 3 is 6 cm. If equal flow rates are to occur at sections 2 and 3, find V2 and V3 is m/s. Given Data: Solution: We know that the rate of flow in the main pipe is equal to the sum of rate of flow through branch pipes. Example 3.11 Fluid is flowing through a tapering pipe having diameters 50 mm and 25 mm at sections 1 and 2 respectively. The discharge through the pipe is 7.5 Lps (i.e., litres per second). The section 1 is 3 m above datum and section 2 is 1.25 m above datum. If the pressure at section 1 is 200 kPa, find the pressure at section 2. The specific gravity of the fluid is 0.9. Given Data: D1 = 50 mm; D2 = 25 mm; Q = 7.5 Lps = 7.5 × 10-3 m3/s; z1 = 3 m; z2 = 1.25 m; P1 = 200 kPa = 300 × 103 N/m2; Specific gravity = 0.9. Solution: Refer Fig.3.20, ⸫ Weight density of fluid, w = 0.9 × 9810 = 8829 N/m3 We know that, Q = A1V1 = A2V2 Now applying the Bernoulli's equation at sections 1 and 2, we get Example 3.12 The kinematic viscosity of a hydraulic oil is 100 cS. If it is flowing in a 20 mm diameter commercial steel pipe, find the friction factor in each case. (a) The velocity is 4.6 m/s. (b) The velocity is 14 m/s. Given Data: v = 100 cS = 1 stroke = 1 × 10-4 m2/s; D = 20 mm. Solution: (a) When the velocity v = 4.6 m/s : First, find the Re number. Since Re < 2000, therefore the flow is laminar. We know that friction factor for the laminar flow, Note The friction factor for the laminar flow can also be obtained using the Moody diagram. (b) When the velocity v = 14 m/s : Since Re > 2000, therefore the flow is turbulent. For the turbulent flow, first we have to find the value of relative roughness (ε/D). From Table 3.1, for commercial steel pipe, ε = 0.046 mm. Now using the Moody diagram (Fig.3.16), by locating the Re and ɛ/D values, we get the projected friction factor value as 0.034 Ans. Example 3.13 Hydraulic oil of kinematic viscosity 0.9 strokes, flows through a 35 mm diameter pipe at a velocity of 4 m/s for a length of 100 m. Find the head loss due to friction (in units of bar). Assume specific gravity of oil as 0.90. Given Data: v = 0.9 stroke = 0.9 × 10-4 m2/s; D= 35 mm; V = 4 m/s; L = 100 m; Specific gravity = 0.9. Solution : First, find the Re number. Since Re < 2000, therefore the flow is laminar. Since the flow is laminar, the head loss due to friction can be calculated by using the Hagen-Poiseuille equation, Example 3.14 What is the head loss (in units of bars) across a 40 mm wide open gate valve when oil (Sg = 0.90) flows through it at a rate of 0.015 m3/s? The K-factor for wide open gate valve is 0.19. Given Data : D = 40 mm; Wide open gate valve ; Sg = 0.90 or woil = Sg × wwater = 0.9 × 9810 = 8829 N/m3; Q = 0.015 m3/s. Solution: Given that, the K-factor for wide open gate valve = 0.19. We know that the head losses in valves and fittings, The pressure drop (∆P) across the valve is given by, Example 3.15 A hydraulic pump delivers oil at 60 bar, 120 lpm into a circuit laid on a horizontal plane. There are 4 elbows (k = 0.75), one globe valve fully open (k = 10) and a direction control valve (pressure drop 3 bar) with the inside diameter of the pipe as 30 mm. The total length of the straight run pipe is 20 m and the specific gravity of the oil is 0.9. The kinematic viscosity of the oil is 0.0001 m2/s. Determine the pressure in bar at the exit point of the pipe. Given Data: P = 60 bar; Q 120 lpm; D = 30 mm; L = 20 m; S = 0.9; v = 0.0001 m2/s. Solution: Since Re <2000, therefore the flow is laminar. ⸫ Head losses in laminar flow in the pipe is given by ⸫ Total head loss = 20.51 + 39.28 = 59.79 m of oil Equivalent pressure drop, ∆P = woil × (HL)total = (0.9 × 9810) 59.79 = 527885.9 N/m2 or 5.28 bar ⸫ Pressure at the exit point of the pipe = Inlet pressure - Total pressure drop = 60 - 5.28 = 54.72 bar Ans.On Force, Pressure, and Head
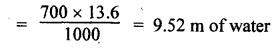
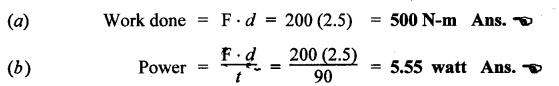

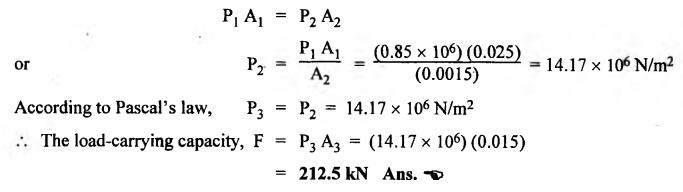
On Reynolds Number and Fluid Flow
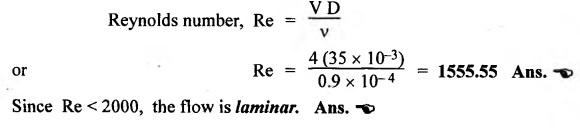
On Flow Rate and Continuity Equation
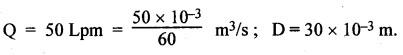
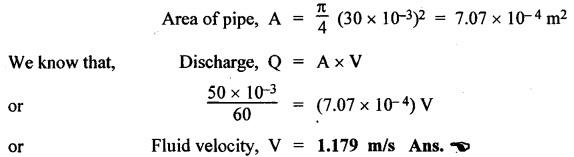
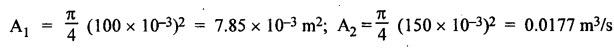
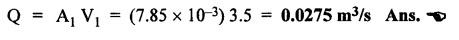
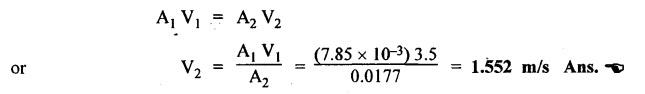
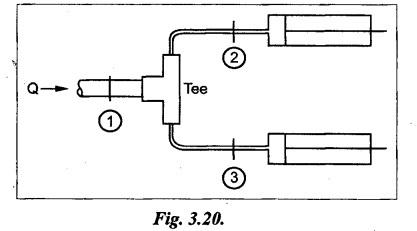
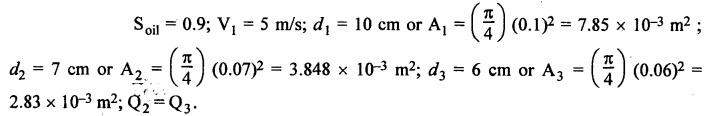
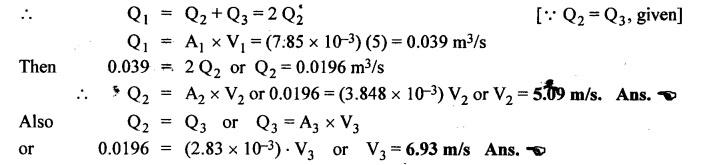
On Bernoulli's Equation
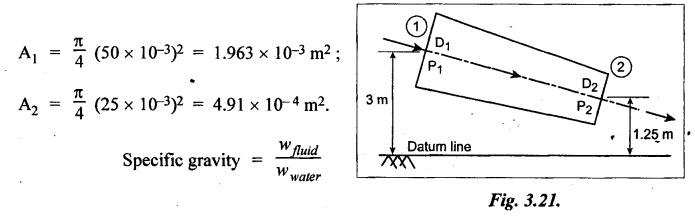
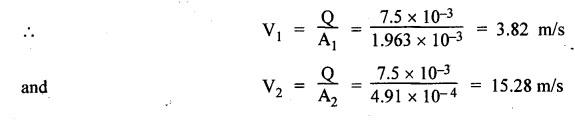
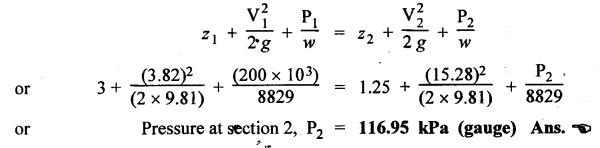
On Darcy's Equation
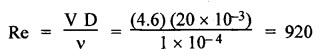
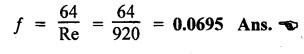
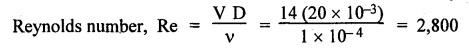
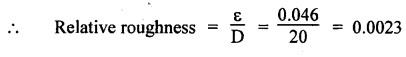
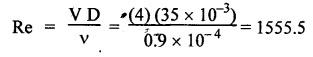
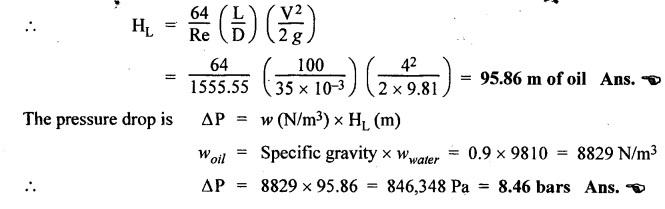
On Losses in Valves and Fittings
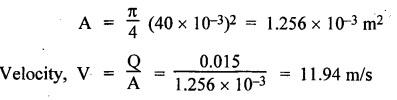
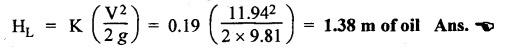

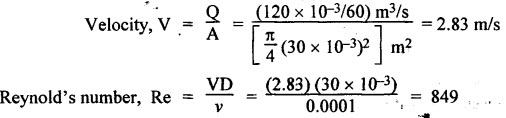

Hydraulics and Pneumatics: Unit I: Fluid Power Priniciples and Hydraulic Pumps : Tag: : Fluid Power Priniciples and Hydraulic Pumps - Hydraulics and Pneumatics - some illustrative example problems
Related Topics
Related Subjects
Hydraulics and Pneumatics
ME3492 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
