Manufacturing Technology: Unit I: Mechanics of Metal Cutting
solved problems on tool life
Mechanics of Metal Cutting - Manufacturing Technology
solved problems on tool life: Mechanics of Metal Cutting - Manufacturing Technology
SOLVED PROBLEMS ON TOOL LIFE Problem 1.20 During a tool life-cutting test on HSS tool material, the following data were recorded. Calculate the values of n and C of Taylor's equation. Given data: T1 = 40 min V1 = 25 m/min T2 = 5 min V2 = 75 m/min Solution: By Taylor's equation Problem 1.21 A cutting tool made of HSS gave a tool life of 50 min when operated at a speed of 200m/min. At what speed should the tool have to be operated in order to have a tool life of 2hrs 15 min. Assume n = 0.185. Given data: T1 = 50 min V1 = 200 m/min T2 = 2 hrs 15 min = 135 min n = 0.185 Solution: From Taylor's equation Problem 1.22 A carbide tool gave a tool life of 200 min at 20 m/min and 28 min at 80 m/min. Compute the (i) tool life equation, and (ii) cutting speed for minimum life. Given data: T1 = 200 min V1 = 20 m/min T2 = 28 min V2 = 80 m/min Solution: Taylor's equation is given by V Tn = C ⸫ n = 0.705 20 × 2000.705 = C C = 838.02 Problem 1.23 A "Through-away" carbide insert was used to machine a steel workpiece with a cutting speed of 60 m/min and a tool life of 40 min. When the speed was increased to 100m/min, the tool life was reduced to 10 min. Using this data, estimate the cutting speed for maximum productivity, if the tool change time is 2 min. Given data: V1 = 60 m/min T1 = 40 min V2 = 100 m/min T2 = 10 min Solution: From Taylor's tool life equation Problem 1.24 A carbide-cutting tool lasted for 150 min while machining mild steel at 35 m/min. If a similar tool is used at 30% higher speed to machine mild steel, calculate the tool life. Also calculate the value of cutting speed if the tool is to machine for 2 hours. Assume n = 0.3 in Taylor's tool life equation VTn = C. Given data: T1 = 150 min V1 = 35 m/min. T2 = 2 hrs = 120 min n = 0.3 Solution: Taylor's equation is given by VTn = C 35 × (150)0.3 = C C = 157.36 When speed is increased by 30% Problem 1.25 The tool life equation for HSS tool is expressed by VT 0.15 = C1 and the tungsten carbide tool is expressed by VT 0.25 = C2. If at a speed of 30 m/min the tool life is 120 min, compare the life of the two tools at a speed of 40 m/min. Given data: V T0.15 = C1 V T 0.25 = C2 V = 30 m/min T = 120 min V' = 40 m/min Solution: For a speed of 30 m/min and a tool life of 120 min: For HSS tool, VT0.15 = C1 30 × (120)0.15 = C1 C1 = 61.52 For tungsten carbide tool, 30 × (120)0.25 = C2 C2 = 99.29 For a speed of 40 m/min: For HSS tool, The tool life of tungsten carbide tool is 2.15 times more than the HSS tool. Ans. Problem 1.26 Calculate the percentage change in cutting speed required to give 70% reduction in tool life. The speed life relationship is given by V Tn = C. Take n = 0.2. Given data: VTn = C n = 0.2 Solution: Problem 1.27 The results of machining steel with two grades of tool materials are given below: 1. What are the standard tool life equations for these two materials? 2. For a 180 minute tool life, which tool is recommended and why? 3. If the tool grinding and changing time is 15 minutes, which cutting speed for the tool 'A' has to be chosen from the two available speeds, 45 m/min, 50m/min?` Solution: (i) Tool life equations are (ii) For T = 180 min Since tool A has greater cutting speed for same tool life, it is recommended. Ans. (iii) For tool A, at V = 45 m/min 45 × (T)0.2 = 100 Since 45 m/min cutting speed gives more tool life, this speed has to be chosen from the two available speeds for tool A. Ans. Problem 1.28 The following equation for tool life was obtained for HSS tool VT0.13 f0.6 d0.3 = C A 60 min tool life was obtained using the following cutting condition. V = 40 m/min, f = 0.25 mm, d = 2 mm Calculate the effect on tool life if speed, feed and depth of cut are together increased by 25% and also if they are increased individually by 25%. Where ƒ = feed, d = depth and V = speed. Solution: The given tool life equation is given by V T0.13 ƒ0.6 d0.3 = C Substituting V, T, ƒ and d values in above equation 40 × 600.13 × 0.250.6 × 20.3 = C C = 36.5 When the speed, feed and depth of cut are together increased by 25% V = 50 m/min, f = 0.3125 mm, d = 2.5 mm Substituting above vales in given equation, Problem 1.29 A cutting tool at 35 m/min gives a life of one hour twenty minutes when operating on roughening cuts. What will be the probable life when engaged on light finishing cuts? Take, n = 0.125 for rough cut & 0.1 for finishing cut. Solution: Taylor's equation is VTn = C For rough cut n = 0.125 V = 35 m/min and T = 1 hr and 20 min = 80 min 35 × 800.125 = C C = 60.53 For finish cut, n = 0.1 V = 35 m/min and C = 60.53 Problem 1.30 The lives of two tools, A and B are governed by equations VT0.125 = 2.5 and VT0.25 = 7 -respectively in a certain machining operation, where V is the cutting speed in m/sec and T is tool life in seconds. (a) Find out the speed V at which both the tool will have the same tool life. Also calculate the corresponding tool life T. (b) If you have to machine at a cutting speed of 1m/s, which one these tools will you choose in order to have less frequent tool changes? Given data: Solution: (a) From equation (1.8), Since both tool having same life, substituting this T value in equation (1.10) (b) V = 1 m/s For tool A, from equation (1.9), 1 × T0.125 = 2.5 ⸫ T = 1525.88 seconds For tool B, from equation (1.10), 1 × T0.25 = 7 ⸫ T = 2401 seconds. Since tool B has greater tool life for the same cutting speed of 1m/s, it has less frequent tool changes and hence it is chosen. Ans. Problem 1.31 Tool life testing on a lathe under dry cutting conditions gave n and C of Taylor's tool life equation as 0.12 and 130 m/min respectively. When a coolant was used, C increased by 10%. Find the percentage increase in tool life with the use of coolant at a cutting speed of 90 m/min. Given data: n =0.12 C = 130 m/min V = 90 m/min Solution: Taylor's tool life equation is given by VTn = C 90 × T0.12 = 130 When coolant was supplied, C increases by 10% Problem 1.32 Cylindrical bars of 100 mm diameter and 576 mm length are turned in a single pass operation. The spindle speed used is 144 rpm, and the total feed is 0.2 mm/rev. Taylor's tool life relationship is VT 0.75 = 75. Where "V" is the cutting speed in m/min and T is tool life in min. calculate the: (i) •_time required for turning one piece. (ii) average tool change time per piece given that it takes 3 min to change the tool each time, and (iii) time required to produce one piece given that the handling time is 4 min. Given data: D = 100 mm L = 576 mm N =144 rpm f = 0:2 mm/rev VT0.75 = 75 Solution: (i) Time required to turn one piece is given by (ii) Average total change time per piece 45.24 × T0.75 = 75 ⸫ T = 1.962 min Hence a break of 3 min to be given after 1.962 min for changing the tool, the number of times the tool needed to be changed during machining for 20 min. (iii) If handling time is 4 min, the total time required to produce one piece = handling time + production time Production time = machining time + total change time= 20 + 33 = 53 min Problem 1.33 If under a given condition of plain turning, the life of the cutting tool decreased by 50% due to increase in the cutting velocity by 20%, by what percentage will the life of that tool increase due to reduction in the cutting velocity by 20% from its original value? Given data: T decreases by 50% V increased by 20% Solution: From Taylor's tool life equation, Problem 1.34 If the relationship for HSS tools is VT1/8 = C1 and for tungsten carbide tools is VT1/5 = C2 and assuming that at a speed of 25 m/min, the tool life was 3 hours in each case, compare their cutting lives at 32 m/min. Given data: V = 25 m/min T = 3 hrs = 180 min V' = 32 m/min Solution: From equation (1.14), VT1/8 = C1 25 × (180)1/8 = C1 C1 = 47.846 From equation (1.15), VT1/5 = C2 25 × (180)1/5 = C2 C2 = 70.63 For V = 32 m/min From equation (1.14), 32 × T1/8 = 47.846 ⸫ T = 24.97 min From equation (1.15), 32 × T1/5 = 70.63 (⸪ C1 = 47.846) ⸫ T = 52.38 min (⸪ C2 = 70.63) For 32 m/min cutting speed, second equation i.e. VT1/5 = C2 gives better life. Ans. Problem 1.35 In a tool wear test with high-speed steel cutting tool, the following data were recorded. Compute the Taylor's equation. Given data: T1 = 30 min V1 = 25 m/min T2 = 2 min V2 = 70 m/min Solution: According Taylor's equation, VTn = C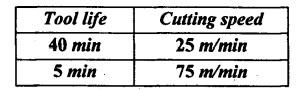
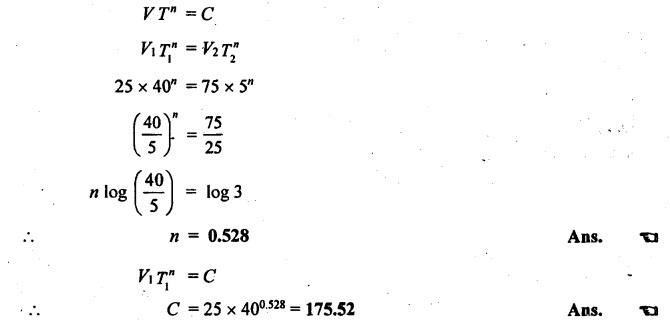

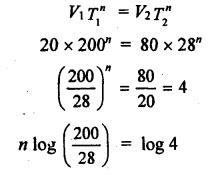

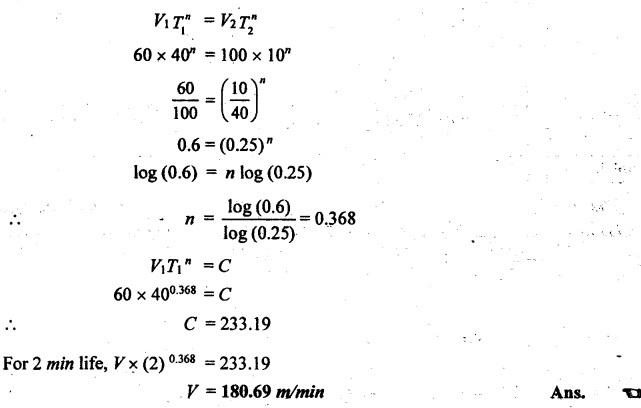


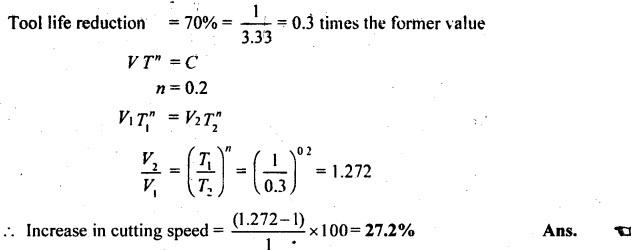


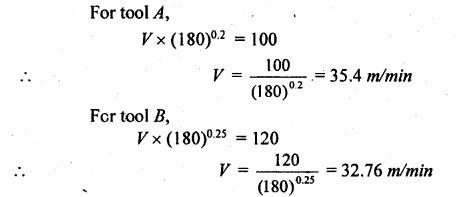
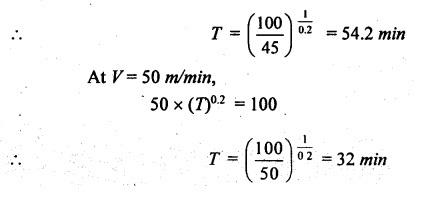

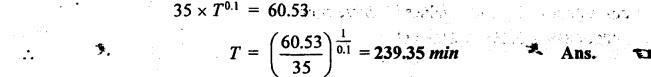

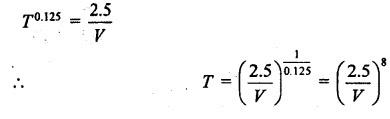
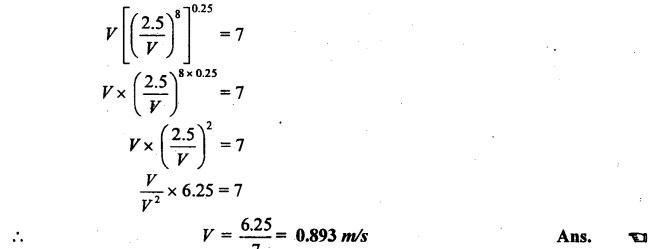
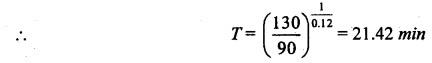
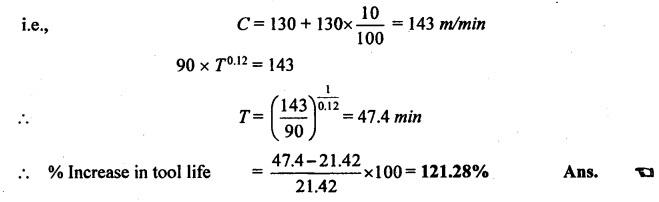
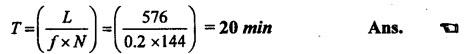
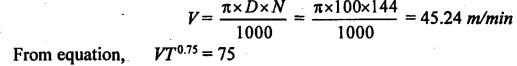
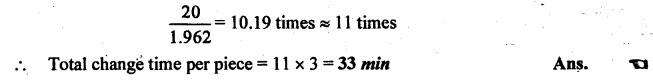
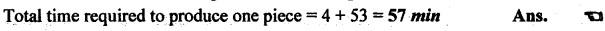



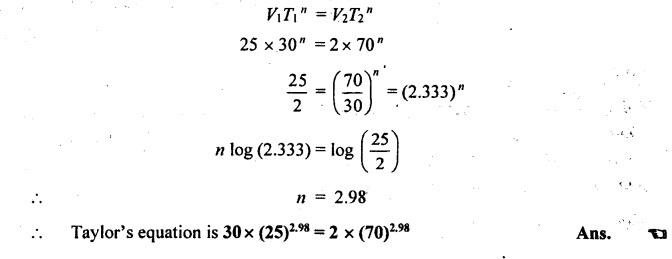
Manufacturing Technology: Unit I: Mechanics of Metal Cutting : Tag: : Mechanics of Metal Cutting - Manufacturing Technology - solved problems on tool life
Related Topics
Related Subjects
Manufacturing Technology
ME3493 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
