Engineering Thermodynamics: Unit III: Availability and Applications of II Law
Solved Problems on Entropy
Thermodynamics
Solved Problems on Entropy: Availability and Applications of II Law - Engineering Thermodynamics
SOLVED PROBLEMS ON ENTROPY Problem 3.1 1.6 kg of air compressed according to the law pV1.3 = C form a pressure of 1.2 bar and temperature of 20°C to a pressure of 17.5 bar. Calculate the (a) final volume and temperature (b) work done (c) heat transferred and (d) change in entropy. Given data: m = 1.6 kg pV1.3 = C ⸫ n = 1.3 p1 = 1.2 bar = 120 kN/m2 T1 = 20°C = 20 + 273 = 293 K p2 = 17.5 bar = 1750 kN/m2 To find: V2, T2, W, Q and ΔS Solution: From general gas equation, From polytropic process relation, Problem 3.2 Air expands from 11 bar at 550°C to a pressure of 3 bar adiabatically. Determine the temperature at the end of expansion and work done. Find also the change in entropy. Given data: p1 = 11 bar = 1100 kN/m2 T1 = 550°C = 550 + 273 = 823 K p2 = 3 bar = 300 kN/m2 Process: Adiabatic To find: T2, W and ΔS Solution: p, V and T relation for adiabatic process is given by Problem 3.3 1 kg of air is compressed according to the law pV1.25 = C from 1 bar and 15°C to 17 bar. Calculate the change in entropy. Cp = 1.005 kJ/KgK and Cv = 0.72 kJ/kgK. Given data: m = 1kg pV1.25 = C; So, n = 1.25 p1 = 1 bar = 100 kN/m2 p2 = 17 bar = 1700 kN/m2 T1 = 15°C = 15 + 273 = 288 K Cp = 1.005 kJ/kgK Cv = 0.72 kJ/kgK ⸫ R = Cp - Cv = 1.005 - 0.72 = 0.285 kJ/kgK To find: Change in entropy, ΔS Solution: From polytropic relation, Problem 3.4 One kg of air in a closed system initially at 5°C occupying a volume of 0.3 m3 undergoes a constant pressure heating process to 100°C. There is no work other than pdV work. Find the work transfer, heat transfer and entropy change of the gas. Given data: m = 1 kg T1 = 5°C = 5 + 273 = 278 K V1 = 0.3 m3 T2 = 100°C = 100 + 273 = 373 K To find: W, Q and ΔS Solution: For constant pressure process, Work transfer, W = p (V2 - V1) = mR (T2 - T1) = 1 × 0.287 (373 - 278) = 27.27 kJ Ans. Heat transfer, Q = mCp (T2 - T1) = 1 × 1.005 (373 - 278) = 95.48 kJ Ans. Change in entropy, Problem 3.5 Ten grams of water at 20°C is converted into ice at -10°C at constant atmospheric pressure. Assuming the specific heat of liquid water to remain constant at 4.2 J/gK and that of ice to be half of this value and taking the latent heat of fusion of ice at 0°C to be 335 J/g. Calculate the total entropy change of the system if Cp of ice = 2.093 J/gK. Given data: mw = 10 g Tw = 20°C Tice = -10°C Cpw = 4.2 J/g K hfg = 335 J/g Cpice = 2.093 J/gK To find: Change in entropy, ΔS Solution: Heat absorbed from the water to form 10 g of ice, Entropy change of the atmosphere, Entropy change of the system from 20°C to 0°C Problem 3.6 A constant volume chamber of 0.3 m3 capacity contains 1 kg of air at 56°C. Heat is transferred to the air until the temperature is 100°C. Find the work transfer, heat transfer and the change in internal energy, enthalpy and entropy. Given data: V1 = 0.3 m3 m = 1 kg T1 = 56°C = 329K T2 = 100°C = 373K To find: W, Q, ΔU, ΔH and ΔS Solution: Work transfer, W = 0 for constant volume process Ans. Heat transfer = Change in internal energy Q = ΔU = mCv (T2 - T1) = 1 × 0.718 (100 - 56) = 31.59 kJ Ans. Change in enthalpy, ΔH = ΔU = 31.59 kJ Ans. Problem 3.7 10 kg of water 90°C mixes with 2.5 kg of water at 20°C under adiabatic condition. Find the final temperature and entropy generation. Given data: m1 = 10 kg T1 = 90°C = 90 + 273 = 363 K m2 = 2.5 kg T2 = 20°C = 20 + 273 = 293 K To find: Tf and ΔS Solution: Problem 3.8 In a certain heat exchanger, 45 kg/min of water is to be heated from 60° C to 115° C by hot gases which enter the heat exchanges at 225 K and flow at the rate of 90 kg/min. Compute the net change of entropy. Assume specific heat for water and gases as 4.18 kJ/kgK and 1.045 kJ/kgK. Given data: To find: Net change of entropy, ΔS Solution: By energy balance, Heat gained by water = Heat given out by gas Problem 3.9 A perfect gas is contained in a cylinder and undergoes a controlled expansion according to the law p =A+ BV, where A and B are constants. p be the pressure in kgf/cm2 and v be the volume in m3. The initial and final pressures are 8.4 kgf/cm2 and 2.8 kgf/cm2 and the corresponding volumes are 0.056 m3 and 0.168 m3. Assume y = 1.39, R = 0.28 kJ/kgK. The initial temperature is 15°C. Determine the (a) work done by the gas (b) heat transferred during the process in magnitude and direction (c) change in entropy per kg of gas during expansion (d) maximum value of internal energy per kg reckoned from 0°C. Given data: p = A + BV p1 = 8.4 kgf/cm2 = 8.4 × 104 = 84000 kgf/m2 = 840000 N/m2 p2 = 2.8 kgf/cm2 = 2.8 × 104 = 28000 kgf/m2 = 280000 N/m2 V1 = 0.056 m3 V2 = 0.168 m3 γ = 1.39 R = 0.28 kJ/kg K T1 = 15°C = 15 + 273 = 288 K To find: W, Q, ΔS and ΔU Solution: p = A + BV ... (3.18) At p1 = 8.4 kgf/cm2 and V1 = 0.056 m3 8.4 = A + 0.056 B ... (3.19) At p2 = 2.8 kgf/cm2 and V2 = 0.168 m3 2.8 = A + 0.168 B ... (3.20) Subtracting equation (3.19) from (3.20), -5.6 = 0.112 B B = -50 A = 11.2 ⸫ Equation (3.18) becomes, p = 11.2 - 50 V Substituting (3.21) in (3.18), For getting maximum temperature, differentiating the equation (3.22) and equating it to zero. 2pdp - Adp = BmRdT BmRdT = 2 pdp - Adp BmRdT = (2p - A) dp















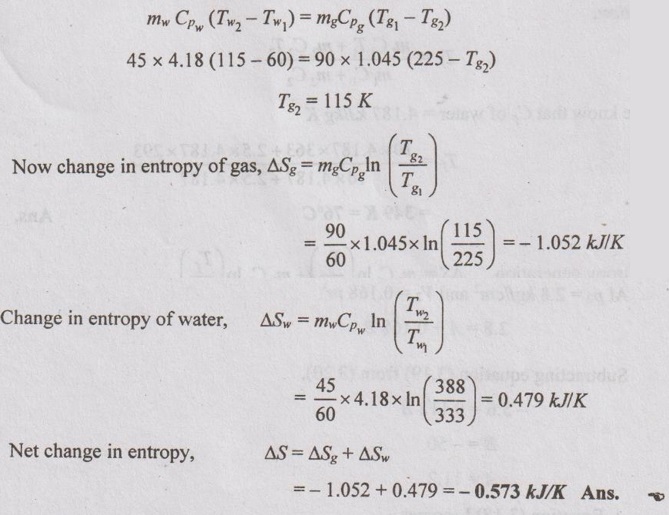



Engineering Thermodynamics: Unit III: Availability and Applications of II Law : Tag: : Thermodynamics - Solved Problems on Entropy
Related Topics
Related Subjects
Engineering Thermodynamics
ME3391 3rd semester Mechanical Dept | 2021 Regulation | 3rd Semester Mechanical Dept 2021 Regulation
