Manufacturing Technology: Unit I: Mechanics of Metal Cutting
solved problems on cutting forces
Mechanics of Metal Cutting - Manufacturing Technology
solved problems on cutting forces: Mechanics of Metal Cutting - Manufacturing Technology
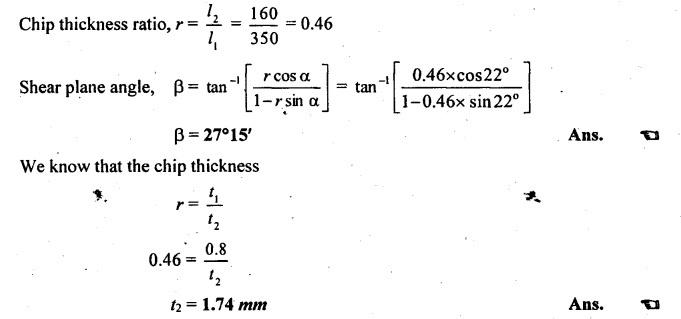
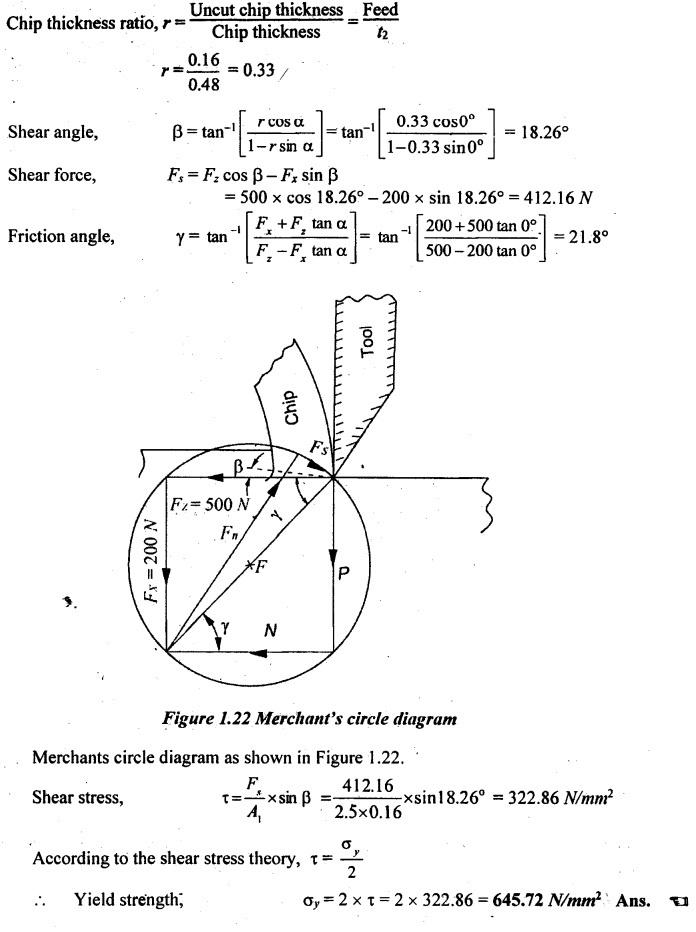
SOLVED PROBLEMS ON CUTTING FORCES Problem 1.1 A mild steel workpiece of 60 mm diameter is to be turned with an orthogonal tool to a feed rate of 0.92 mm/revolution and at 75 rpm. If the chip thickness is 2 mm, determine the chip thickness ratio and length of chip removed in one minute. Assume a condition of continuous chip. Given data: D = 60 mm t1 = 0.92 mm/rev N = 75 rpm t2 = 2 mm Solution: Problem 1.2 During an orthogonal cutting a chip length of 160 mm was obtained from an uncut chip length of 350 mm. The cutting tool has 22° rake angle and a depth of cut is 0.8 mm. Determine the shear plane angle and chip thickness. Given data: l2 = 160 mm l1 = 350 mm α = 22° t1 = 0.8 mm Solution: Problem 1.3 In an orthogonal cutting process, the following observations were made Depth of cut = 0.25 mm Chip thickness ratio = 0.45 Width of cut = 4 mm Cutting velocity = 40 m/min Cutting force component parallel to cutting velocity vector = 1150 N Cutting force component normal to cutting velocity vector = 140 N Rake angle = 18° Determine the resultant cutting force, power of cutting, shear plane angle, friction angle and force component parallel to shear plane. Given data: t1 = 0.25 mm r = 0.45 mm b = 4 mm V = 40 m/min Fz = 1150 N Fx = 140 N α = 18° Solution: Problem 1.4 A seamless tube 32 mm outside diameter is turned on a lathe. The cutting velocity of the tool relative to the workpiece is 10m/min. Rake angle = 35°, depth of cut = 0.125 m, length of chip = 60 mm, horizontal cutting force of the tool on the workpiece = 200 N. The cutting force required to hold the tool against the workpiece = 80 N. Calculate the (i) co-efficient of friction (ii) chip thickness ratio (iii) shear plane angle (iv) velocity relative to the tool, and (v) velocity of chip relative to the workpiece. Given data: D = 32 mm V = 10 m/min α = 35° t1 = 0.125 mm l2 = 60 mm Fz = 200 N Fx = 80 N Solution: Problem 1.5 The following data from the orthogonal cutting test is available. Rake angle = 10° Chip thickness ratio = 0.35 Uncut chip thickness = 0.51 mm Width of cut = 3 mm Yield shear stress of work material = 285 N/mm2 Mean friction coefficient on tool face = 0.65. Determine the (i) cutting force, (ii) radial force, (iii) normal force on the tool, and (iv) shear force on the tool. Given data: α = 10° r = 0.35 t1 = 0.51 mm b = 3 mm τ = 285 N/mm2 μ = 0.65 Solution: Problem 1.6 The following observations are made from a metal cutting test Cutting force = 180 kg Feed = 5 cuts/min Depth of cut = 5 mm Cutting speed = 30 m/min If overall efficiency of machine is 70%, determine the (i) normal pressure on chip, (ii) power required at motor. Given data: F2 = 180 kg Feed = 5 cuts/min t1 = 5 mm V = 30 m/min η = 70% Solution: Problem 1.7 In an orthogonal cutting, experiment with a tool of rake angle a = 7°, the chip thickness was found to be 2.5 mm when the uncut chip thickness was set to 1 mm. (i) Find the shear angle, β (ii) Find the friction angle γ assuming that Merchant's formula holds good. Given data: α = 7° t2 = 2.5 mm t1 = 1 mm Solution: Problem 1.8 In an orthogonal cutting operation on a workpiece of width 2.5 mm, the uncut chip thickness was 0.25 mm and the tool rake angle was 0°. It was observed that the chip thickness was 1.25 mm. The cutting force was measured to be 900 N and the thrust force was found to be 810 N. (i) Find the shear strength of the workpiece material. (ii) If the coefficient of friction between the chip and the tool was 0.5 what is the machining constant? Given data: b = 2.5 mm t1 = 0.25 mm α = 0° t2 = 1.25 mm F2 = 900 N Fx = 810 N μ = 0.5 Solution: Shear force, Fs = Fz cos β - Fx sin β = 900 cos 11.31°- 810 sin 11.31° = 723.67 N Problem 1.9 While turning a C15 steel rod of 160 mm diameter at 315 rpm, 2.5 mm depth of cut and fed rate of 0.16 mm/rev by tool geometry 0, 10, 8, 9, 15, 75, 0. The following observations were made. Tangential component (P) of the cutting force = 500 N Arial component (P) of the cutting force = 200 N Chip thickness = 0.48 mm (a) Draw schematically the Merchant's circle diagram for the cutting forces in the present case and (b) Determine the dynamic yield strength of the present work material. Given data: D = 160 mm N = 315 rpm d = 2.5 mm Feed rate = 0.16 mm/rev α = 0° (from tool signature) Fz = Pz = 500 N Fx = Px = 200 N t2 = 0.48 mm Solution: Problem 1.10 Calculate the (i) metal removal rate, (ii) specific cutting pressure for the following cutting conditions: Work material = Steel Ultimate tensile strength = 980 MN/m2 Tool material = HSS Depth of cut = 1.6 mm Feed = 0.8 mm/rev Cutting speed = 5.5 m/min Power consumed = 0.67 kW Given Data: σt = 980 MN/m2 = 980 N/mm2 d = 1.6 mm Feed, f = 0.8 mm/rev V = 5.5 m/min Power = 0.67 kW Solution: Problem 1.11 A tube is orthogonal machined in a lathe to reduce its length under the following conditions. Outside diameter of the tube = 100 mm Inside diameter of the tube =་ 96 mm RPM of the workpiece =120 Longitudinal feed = 0.5 mm/rev Cutting ratio = 0.5 mm/rev Tangential force = 800 N Axial force = 600 N Calculate the (i) chip velocity in m/min (ii) power consumption in kW. Given data: Do = 100 mm Di = 96 mm N = 120 rpm f = 0.5 mm/rev r = 0.3 Fz = 800 N Fx = 600 N Solution: Problem 1.12 A lathe while running consumes 2000 W when cutting a steel specimen at 30 m/min. Determine the cutting force and torque at the spindle running at 120 rpm. Also determine the specific power consumption if the depth of cut is 4 mm and feed is 0.25 mm/rev. Given data: P = 2000 W V = 30 m/min N = 120 rpm d = 4 mm f = 0.25 mm/rev Solution: We know that power consumed, P = Cutting force, (F) × Velocity,(V) 2000 = F × 30 Problem 1.13 Mild steel is being machined at a cutting speed of 120 m/min with a feed rate of 0.6mm/rev. If the power coefficient for this operation is 0.2 HP/cm3/min and maximum power available at the machine spindle is 8 HP, determine the following: (a) maximum metal removal rate (b) depth of cut (c) cutting force (d) normal pressure on chip. Given data: V = 120 m/min = 120 × 100 cm/ min f = 0.6 mm/rev = 0.06 cm/rev Power required = 0.2 HP/cm3/min Power available = 8 HP Solution: Depth of cut: Problem 1.14 An orthogonal test is conducted on a mild steel tube of size 225 mm diameter and 5mm thickness. The velocity of cutting is 105 m/min and the feed rate is 0.21 mm/rev. The following observations were made. Cutting force = 2300 N Feed force = 825 N Chip thickness = 0.3 mm Contact length = 0.9 mm Horse power = 3 kW. Rake angle = -10° Determine the shear strain, and energy per unit volume. Given data: D = 225 mm t = 5 mm V = 105 m/min f = 0.21 mm/rev Fx = 2300 N Fx = 825 N t2 = 0.3 mm HP = 3 kW α = -10° Solution: Problem 1.15 Mild steel is being machined orthogonally and the following results are obtained: Cutting force = 1000 N Feed force = 625 N Cutting velocity = 165 m/min Rake angle = 10° Shear plane angle = 19° Determine the following: (i) shear velocity, (ii) chip flow velocity, (iii) work done per minute in shearing the metal and work done against friction and (iv) show that the work input is equal to the sum of work done in shearing and against friction. Given data: Fz = 1000 N Fx = 625 N V = 165 m/min α = 10° β = 19° Solution: It shows that the work input is almost equal to the sum of work done in shearing and work done against friction within limits of accuracy. Problem 1.16 The following data from an orthogonal cutting test is available Rake angle = 15° Chip thickness ratio = 0.383 Uncut chip thickness 0.5 mm Width of cut, b = 3 mm Yield stress of material in shear = 280 N/mm2. Average coefficient of friction on the tool face as 0.7 Determine the normal and tangential forces on the tool face. Similar to Problem 1.5 on Page 1.39. [Ans:- Tangential force or cutting force, Fz = 1404.5 N and Normal force or feed force, N = 511.2 N] Problem 1.17 In an orthogonal cutting operation, the following data have been observed: Uncut chip thickness, t = 0.127 mm Width of cut, b = 6.35 mm Cutting speed, V = 2 m/s Rake angle, α = 20° Cutting force, Fc = 567 N Thrust force = 227 N Chip thickness, t2 = 0.228 mm Determine the shear angle, friction angle, shear stress along the shear plane and the power for the cutting operation. Given data: t1 = 0.127 mm b = 6.35 mm V = 2 m/s α = 20° Fz = 567 N Fx = 227 N t2 = 0.228 mm Solution: Problem 1.18 During a metal cutting test under orthogonal conditions, it was found that cutting force is 1100 N and feed force 700 N, when cutting at 165 m/min. The rake angle of tool is 10° and shear plane angle was found to be at 19o. Determine the following: (a) shearing velocity (b) chip flow velocity (c) work done per min in shearing the metal and work done against friction. Similar to Problem 1.15 on Page 1.49. [Ans:- Shearing velocity, Vs = 164.5 m/min, Chip flow velocity, Vc = 54.38 m/min, Work done in shear, Ws = 2.226 kW, Work done against friction, Wƒ = 0.798 kW] Problem 1.19 A 100 mm diameter bar is turned by means of a tool for which ϕ = 90° and α = 15° The depth of cut is 5 mm and the feed is 0.25 mm/rev. If the mean length of a cut chip representing one rotation of the workpiece is 92 mm, find the shear plane angle. Given data: α = 15° ϕ = 90° d = 5 mm t1 = 0.25 mm/rev t2 = 92 mm Solution: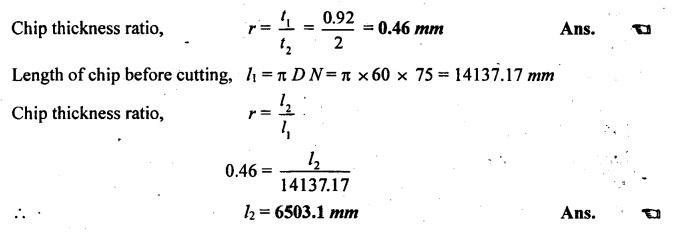





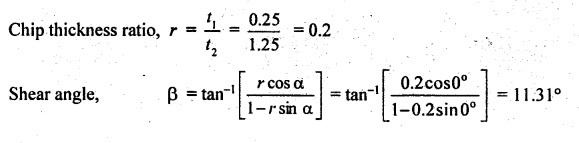
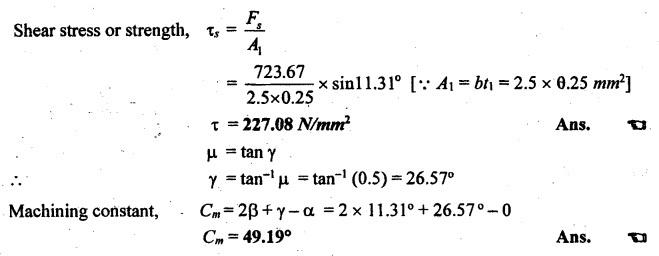
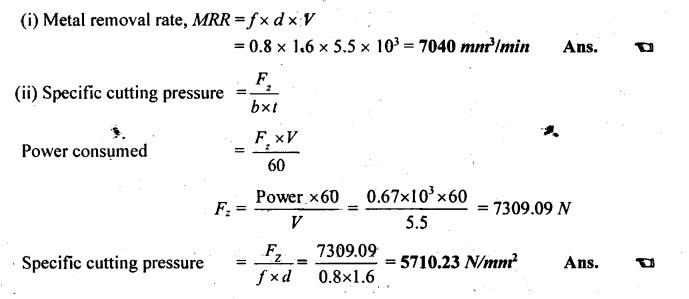



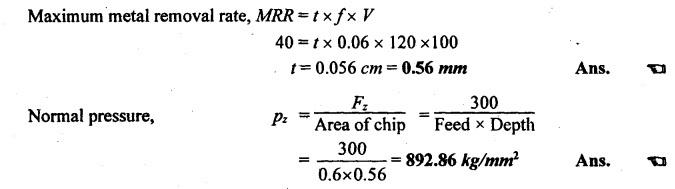



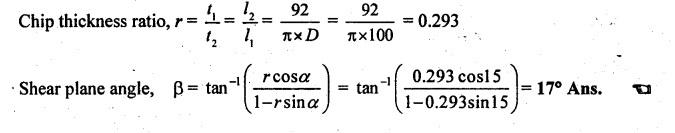
Manufacturing Technology: Unit I: Mechanics of Metal Cutting : Tag: : Mechanics of Metal Cutting - Manufacturing Technology - solved problems on cutting forces
Related Topics
Related Subjects
Manufacturing Technology
ME3493 4th semester Mechanical Dept | 2021 Regulation | 4th Semester Mechanical Dept 2021 Regulation
