Engineering Physics: Unit I: Mechanics
Solved Problems of Mechanics
Engineering Physics
SOLVED PROBLEMS of Mechanics: Chapter 1: Engineering Physics
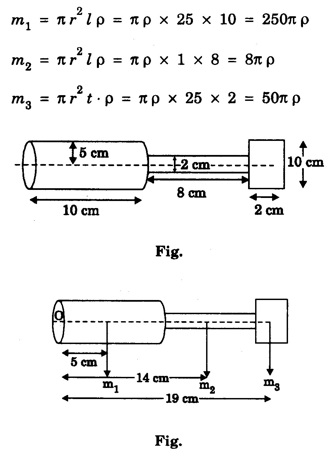
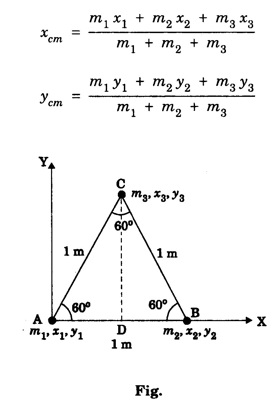
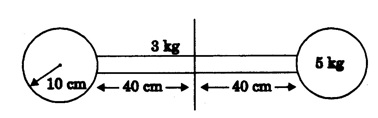
SOLVED PROBLEMS Problem 1.1 Give the location of centre of mass of a (i) hollow sphere (ii) hollow cylinder (iii) hollow cube (iv) ring (v) solid cylinder (vi) solid cube. Does the centre of mass of a body necessarily lie inside the body. Solution: (i) CM of hollow sphere is located at its centre. (ii) CM of hollow cylinder is located at the mid point of its axis of symmetry. (iii) CM of hollow cube lies at its geometric centre. (iv) CM of ring is at the centre of ring. (v) CM of solid cylinder at the mind point of its axis of symmetry. (vi) CM of solid cylinder at its geometric centre. It is not necessary that the CM of a body lie inside the body. Problem 1.2 In an HCI molecule, the separation between the nuclei of two atoms is 1.27 A. Find the position of CM of the molecule. Given that chlorine atom is 35.5 times heavier than hydrogen atom and that nearly entire mass of the atom is concentrated in it, nucleus. Solution: Let the mass of hydrogen atom m1 = m and it is located at x1 = 0 The mass of chlorine atom m2 = 35.5 m and it is located at x2 = 1.27 Å = 1.27 ×10-10 m If X is the distance of the CM of HCl molecule, then Hence, CM of HCL molecule is situated on the line joining the two nuclei and at a distance of 1.235 × 10-10m (1.235 Å) from hydrogen nucleus. Problem 1.3 A machine part is shown in the fig. It consists of a 10 cm long and 10 cm diameter solid cylinder attached at one end of a 8 cm long, 2 cm diameter cylindrical rod. At other end of the rod, a 10 cm diameter and 2 cm wide disc is attached. Find the centre of mass of the machine part assuming it to be made of the homogeneous material. Solution: We measure the distance from free end of the cylinder. Let ρ be the density (homogeneous) of the system, then the masses of three components are given by The distances from O at which the masses are concentrated are x1 = 5 cm. x2 = 14 cm, x3 = 19 cm. So distance of centre of mass from O is given by Problem 1.4 Locate the centre of mass of a system of particles of masses m1 = 1 kg, m2 = 2 kg and m3 = 3 kg, situated at the corners of an equilateral triangle of side 1.0 m. Solution: We have from fig. The centre of mass is given by In this case m1 = 1 kg, m2 = 2 kg, m3 = 3 kg x1 = 0, y1 = 0, x2 = 1, y2 = 0; which gives the coordinates of centre of mass as (3.5/6, √3/4) Problem 1.5 The radius of gyration of a disc about its centre of mass is 1.41 m. If the mass of the disc is 1 kg, what is its moment of inertia? Solution: I = MK2 Here M = 1 kg , K = 1.41 m therefore, I = (1) (1.41)2 = 2 kg-m2 Problem 1.6 A body of mass 50 g is revolving about an axis in a circular path. The distance of the centre of mass of the body from the axis of rotation is 50 cm. Find the moment of inertia of the body. Solution: Assuming the body as a particle, we have, I = MR2 = (50 × 10-3) (50 × 10-2 )2 = 1.25 × 10-2 kg. m2 Note. If the body has a finite size, then one has to use the theorem of parallel axis. Problem 1.7 Two masses each of 1 kg mass are attached at the ends of a light rod of length 2 m. Assuming the masses as point masses find moment of inertia of the system about an axis passing through the middle point of the connecting rod and perpendicular to the rod. The mass of the connecting rod is negligible. Solution: I = Σ r2 = m1 r12 + m2 r22 = m1 = m2 = 1 kg Here r1 = r2 = 1m Therefore, I = 1 × 12 + 1 × 12 = 2 kg-m2 Problem 1.8 Find the moment of inertia about the geometric centre of the given structure made up of one thin rod connecting two similar solid spheres as shown in figure. Solution: The structure is made up of three objects; one thin rod and two solid spheres. Mass of the rod, M = 3 kg and Total length of the rod, l = 80 cm = 0.8 m Moment of inertia of the rod about its centre of mass Irod = M l /12 Irod = 1 /12 × 3 × (0.8)2 = 1/4 × 0.64 Irod = 0.164 kg m2 Mass of the sphere, M = 5 kg Radius of the sphere, R = 10 cm = 0.1 m Moment of inertia of the sphere about its centre of mass Ic = 2/5 MR2 Moment of inertia of the sphere about geometric centre of the structure is, Isph = Ic + Ma2 where, a = 40 cm + 10 cm = 50 cm = 0.5 m Isph = 2/5 MR2 + Ma2 Isph = 2/5 × 5 × (0.1)2 + 5 (0.5)2 Isph = (2 × 0.01) + (0.1)2 + 5 (0.5)2 Isph = (2 × 0.01) + (5 × 0.25) = 0.02 + 1.25 Isph = 1.27 kg m2 As there are one rod and two similar solid spheres we can write the total moment of inertia (I) of the given geometric structure as, I = I rod + (2 × Isph) I = (0.16) + (2 × 1.27) = 0.16 + 2.54 Problem 1.9 A flywheel is a uniform disc of mass 72 kg and radius 50. cm. Calculate (a) moment of inertia (b) its kinetic energy when it is rotating at 70 r.p.m. Solution: (a) M.I. of the flywheel = MR2/2 = 72 × (0.5)2/2 = 72 × 0.5 × 0.5/2 = 9 kg-m2 (b) K.E. of rotation Problem 1.10 A hollow sphere of radius r1 and a solid sphere of radius r2 have some masses and moments of inertia. Find the ratio of their radii. Solution: Assuming hollow sphere to be of negligibly thin wall, it is equivalent to a spherical shell. Problem 1.11 A wheel in the form of uniform disc of diameter one metre and mass 100 kg is rolling on a horizontal plane with a speed of 5 metre per second. Find the kinetic energy of the wheel. Solution: The kinetic energy of the wheel is partly due to translatory motion and partly due to rotary motion Kinetic energy of translation = 1/2mv2 Problem 1.12 Find the rotational kinetic energy of a ring of mass 9 kg and radius 3 m rotating with 240 rpm about an axis passing through its centre and perpendicular to its plane. (rpm is a unit of speed of rotation which means revolutions per minute). Solution: The rotational kinetic energy is, KE = 1/2 I ω2 The moment of inertia of the ring is, I = MR2 I = 9 × 32 = 9 × 9 = 81 kg m2 The angular speed of the ring is, KE = 1/2 × 81 × 64 × (π)2 = 2592 × (π)2 KE ≈ 25920 J ⸪ (π)2 ≈ 10 KE = 25.920 kJ Problem 1.13 A constant torque of 400 N-m turns a wheel about its centre. The moment of inertia of wheel about this axis is 20 kg-m2. Calculate (i) angular acceleration (ii) angular velocity and the KE gained in 2s starting from rest. Solution: (i) Since τ = Iα α = τ / l = 400/20 m α = 20 rad s-2 (ii) Using ω = ω0 + α t Assuming ω0 = 0, ω = α t = 20 × 2 = 40 rad s-1 (iii) Assuming ω0 = 0 Problem 1.14 Calculate the angular momentum of a disc whose rotational kinetic energy is 10 kJ and moment of inertia about its axis of rotation is 4.5 x 10-4 kg-m2. Solution: Problem 1.15 A small object of mass 20 kg is rotating in a circle of diameter 0.20 m at the rate of 2000 rev / min. Find the rotational kinetic energy of the object. Solution: Here M = 20 kg, radius r = 0.02/2 = -0.10 km ∴ Moment of inertia, I = MR2 = 20 × (0.10)2 = 0.20 kg-m2 Problem 1.16 A body of mass 20 kg is rotating in a circular path of diameter 0.20 m at the rate of 100 revolutions in 3 second. Find (i) Rotational kinetic energy of the body (ii) Angular momentum of the body (π2 = 9.86) Solution: Mass of body M = 20 kg radius of circular path, r = 0.20/2 = 0.10 m No. of revolutions per second n = 100/3 rev/sec. ∴ Angular velocity ω = 2 πn = 2 π × 100/3 = 200/3 π rad /s Moment of inertia of body, I = MR2= 20 × (0.10)2 = 0.20 kg-m2 (1) Rotational kinetic energy, K = 1/2 I ω2 = 4.382 × 103 Joule (ii) Angular momentum of body, J = I ω = 41.87 kg-m2/s Problem 1.17 A mass of 2 kg is rotating in a circular path of radius 0.8 m with an angular velocity of 44 rad/s. If the radius of path becomes 1.0 m find the new angular velocity. Solution: The angular momentum J of mass is conserved i.e. J = I ω = constant i.e. I1 ω1 = I2 ω2 Here I1 = mr12 = 2 × (0.8)2 = 1.28 kg-m2, ω1 = 44 rad/s I2 = mr22 = 2 × (1.0)2 = 2 kg-m2 Problem 1.18 A solid cylinder of mass 25 kg rotates about its axis with angular speed 125 s-1. The radius of the cylinder is 0.5 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of angular momentum of the cylinder about its axis? Solution: Mass of cylinder M = 25 kg angular speed ω = 125 s-1 radius of cylinder R = 0.5 m ∴ Moment of inertia of the cylinder about its axis = 3.125 kg m2 ∴ K.E. of rotation, = 1/2 I ω2 = 2.44 × 104 J Angular momentum, L = I ω = 3.125 × 125 = 390.6 Js Problem 1.19 A circular metal hoop of mass 100 g and radius 10 cm rotates about its centre at the rate of 10 rotations per second. The axis of rotation is normal to the plane of| the hoop. Find (a) Moment of inertia about the axis of rotation. (b) Torque required to increase in 10 s the rate of rotation from 10 to 20 per second. Solution: (a) I = MR2 = 0.1 × 0.12 = 1 × 10-3 kg-m3 (b) Initial angular momentum L1 = I ω1 = (1 × 10-3) × (2 π ×10) = 24 π × 10-2 J-s Final angular momentum L2 = I ω2 = (1 × 10-3) × (2 π ×20) Change in angular momentum = L2 – L1 = 4 π × 10-2 – 2 π × 10-2 = 2 π × 10-2 J-s = 2 π × 10-3 N-m Problem 1.20 A sphere of mass 50 g and radius 8 cm is revolving about an axis in a circular path. The distance of the centre of mass of the body from the axis of rotation is 50 cm. Fird the moment of inertia of the body. Solution: Moment of inertia of the spherical body about in axis passing through its centre of mass, is given by = 1.28 × 10-4 kg-m2 I = Ic + Ma2 = 1.28 × 10-4 + (50 × 10-3) (50 × 10-2)2 = 1.28 × 10-4 + 125 × 10-4 = 1.26 × 10-2 kg-m2 Note: If the size of the body is very small then only the body can be treated as a point mass. Problem 1.21 The angular velocity of a flywheel decreases uniformly from 600 rpm to 300 rpm in 5 s. Find (a) angular acceleration, (b) the number of revolutions made by the wheel in the 5s interval, (c) How many more seconds are required for the wheel to come to rest, (d) if the moment of inertia of the flywheel is 0.5 kg m2, what torque was acting? Solution: = – 6.28 rad s-2 (b) Let the number of revolutions done be n. Since the angle turned in 5s is 2πn rad on using the relation n = 37.5 rev (c) Suppose the wheel takes another t seconds to come to rest from the angular speed of 10 π rad s-1, then on using ω2 = ω1 + αt, we have 0 = 10 π - 2 π t t = 5s (d) Using τ = I α with I = 0.5 kg m2 and α = -6.28 rad s-2 , we have find that the retarding torque is τ = 2 × 0.5 × 6.28 = 6.28 N-m Problem 1.22 The angular momentum of rotation of a body 1s 75.36 Js and its rate of rotation is 24 rev per s. Calculate its moment of inertia. Solution: L = Iω Here L = 75.36 Js ω = 2π n = (2 π) (24) rad s-1 = 0.5 kg m2 Problem 1.23 A torque of 75 N·m applied to the rotor of a generator imparts an angular acceleration of 10 rad s-2. What is the moment of inertia of the wheel? Solution: τ = I α Here τ = 75 N.m, α = 10 rad s-2 therefore I = τ/ α =75/10 I = 7.5 kg-m2 Problem 1.24 A fly wheel of moment of inertia 0.3 kg-m3 is rotating at the rate of 200 rpm. What torque is needed to bring it at rest in 10 s? Solution: The torque τ required to produce a retardation 2.093 rad s-2 is given by τ = I α = (0.3) (2.093) = 0.63 N-m Problem 1.25 Consider the earth as a uniform sphere of mass 5.98 × 1024 kg and radius 6.37 × 106 m spinning on its axis at the rate of per day. Find the angular momentum associated with this spinning Solution: Problem 1.26 A grindstone is in the force form of a circular disc of diameter 0.5 m and of mass 10 Kg. What constant torque should be applied so that it attains an angular velocity of 120 rpm in 4 seconds. At what rate is work done by torque at the end of 4 seconds? Solution: Angular velocity after 4 secs ω = 4 π radians / sec. We have, ω = ω0 + α t α = π radian / sec2 τ = I. α The rate at which the work is done = 1.25 π2 watts Problem 1.27 A constant torque of 200 Nm acting on a wheel at rest rotates through an angle of 400 radians in 10 s. Calculate (a) the angular acceleration (b) moment of inertia of the wheel. If the same torque continues to act, what would be angular velocity after 20 seconds? Solution: Let α be the angular acceleration Angular velocity after 20 sec. is ω = ω0 + αt = 0 + 8 × 20 = 160 radian/sec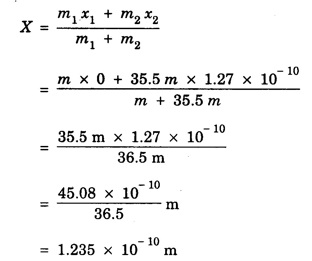

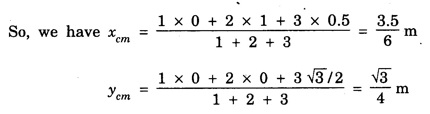


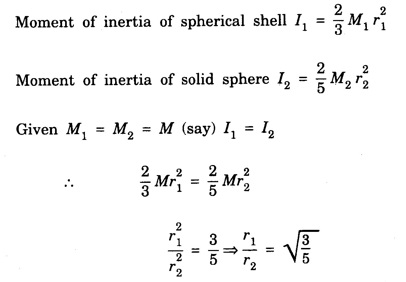


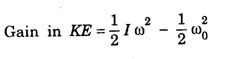
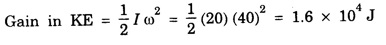


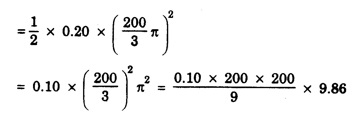

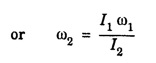
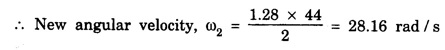
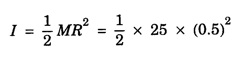
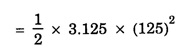
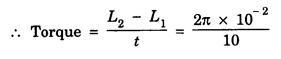
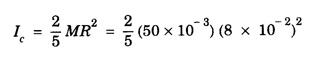








Engineering Physics: Unit I: Mechanics : Tag: : Engineering Physics - Solved Problems of Mechanics
Related Topics
Related Subjects
Engineering Physics
PH3151 1st semester | 2021 Regulation | 1st Semester Common to all Dept 2021 Regulation
